戴榕菁
1. 背景回顾 我之前在讨论广义相对论的对与错【[1],[2],[3]】的时候指出,在相对论被发表的一百多年之前,Soldner就给出了计算地球引力导致来自太空的光线偏移的角度的公式,然后又将它用在了太阳引力导致来自太空的光线偏移角度的计算。只不过,他在发表该公式的文章【[4]】中明确地说了下面这段话: [If it were possible to observe the fixed stars very nearly at the sun, then we would have to take this into consideration. However, as it is well known that this doesn't happen, then also the perturbation of the sun shall be neglected.] 从对于上面这段话的正确的翻译我们可以看出,Soldner明确指出了应用他所计算的太阳引力对于光线影响的数据的前提条件是观察者必须站在太阳的表面,而且他也同时指出因为那是不可能的,所以就没有必要去把他得出的太阳影响的结果当回事儿了。 其实,即便Soldner没有说上面那段话,从他在该文章中给出的推导相关公式所依据的如下面图1中的那幅示意图我们也可以自己得出同样的结论来。 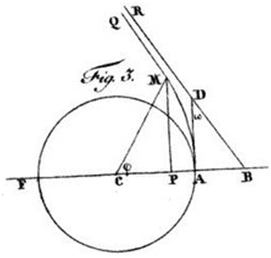 图1. Soldner的原图(来源:https://en.wikisource.org/?curid=755966#/media/File:Ueber_die_Ablenkung_eines_Lichtstrals_von_seiner_geradlinigen_Bewegung.jpg) 但奇怪的是将近一百二十年后,大名鼎鼎的科技界大佬级人物Eddington爵士和戴森(就是那个幻想出戴森球的戴森)在1919年居然用Soldner计算出的太阳造成的光线的偏移角与他们在地球上观察来自遥远的恒星的光线经过太阳时所产生的偏移角度及爱因斯坦用广义相对论计算出的结果进行比对,并得出结论说:爱因斯坦用广义相对论计算出来的偏移角与他们实测的角度完全一致而Soldner的计算结果仅仅是爱因斯坦计算的结果的一半,然后就郑重其事地向全世界宣告:广义相对论打败了牛顿力学! 如我在相关文章中指出的,造成这场乌龙的直接原因有两点:1)Eddington爵士和戴森会莫名其妙地没有按照我在上面引用的Soldner的原文所限定的条件去使用Soldner的计算结果;2)Eddington爵士和戴森居然会没看懂图1所示的Soldner给出的示意图的意思,结果这两位身居作为地球文明的象牙塔的物理学顶端的鼎鼎大名的权威性人物居然没有看出如果要用Soldner的思路来计算地球上观察到的太阳引力造成的来自太空的光线的偏移,他们必须将Solder的原图改为我在相关文章中给出的图2中的示意图,而根据那个示意图,Soldner的计算结果正好与爱因斯坦的计算结果完全一样。 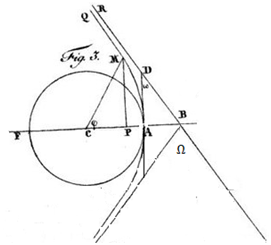
图2. 对Soldner的原图进行的修正(来源:对图1进行的修正) 相应地,如果假想有人确实是在太阳表面来观察来自太空的光线的偏移,那么他得到的结果应该和Soldner按照图1计算的结果以及用广义相对论去计算在太阳表面观察来自太空的光线的偏移所得出的结果都完全一样。 2. 牛顿力学中的光速 在之前的文章中我从考察广义相对论的角度出发指出,尽管广义相对论存在着一些严重的缺陷(比如它对狭义相对论的依赖等等)但它仍与牛顿力学共享一些经验基础,所以广义相对论能够在有关太阳引力对于射到地球上的光线的影响这个问题上得到与基于牛顿力学的Soldner的分析同样的结果。 不过,如果我们把目光转向牛顿力学,有读者们可能不禁会问:不是说相对论颠覆了牛顿力学关于光的运动的看法吗,怎么Soldner用牛顿力学得出的结果会与广义相对论的结果完全一样吗?不仅如此,我们还时常会在网上听到有人提到诸如牛顿力学中的光速为无穷大这样的说法。 其实,光速无穷大是笛卡尔以前的人们曾经有过的看法,等到牛顿的时候,人们不但早已知道光速是有限的,而且那时已知的光速与今天我们所说的光速已经相差不远了【[5]】。 3. Soldner的结果和怎么会广义相对论的一样? 从Soldner的文章中我们可以看出,他在分析中所依据的一个没有明确提到的前提假设是:光在真空中的线速度不受引力的影响,引力改变只是光的方向。当然,我不知道那时的科学界的普遍共识是否就是“光在真空中的线速度不受引力的影响,引力改变只是光的方向”这样的理论,只不过这样的看法显然是Soldner的文章所表现出来的隐性前提假设。 一个世纪之后,爱因斯坦在发表狭义相对论时对于上述的假设所做的改动只是:光速对于所有的观察者来说都一样。虽然爱因斯坦在发表广义相对论之前及之后在引力场对于光速的影响这一点上一直有着摇摆不定的态度,但是在他发表广义相对论之后的官方表述上却一直明确表示光的线速度对于所有的观察者是不变的而光线本身是可以因引力而弯曲的。 所以,在引力对于光线运动的作用这一点上,爱因斯坦与Soldner的区别仅仅是:对于Soldner来说光在真空中的线速度不受引力的影响而爱因斯坦则强调光在引力场中的线速度对于所有观察者来说都是不变的。 但是,在涉及太阳对于经过太阳而到达地球的光线的影响这一点上,因为地球与太阳的相对速度远小于光速,因此“光在真空中的线速度不受引力的影响”和“光在引力场中的线速度对于所有观察者来说都是不变的”之间的区别在他们有关光线偏移角的计算中就表现不出来了----这应该就是的Soldner的结果会和广义相对论的一样的原因。 4.结束语
如果完全按照牛顿将光当成粒子的运动的思路来说,光的线速度在引力的作用下也应该是会改变的。不过,即便是假设引力对光的线速度有影响,在有关太阳(或地球)的引力对于光线所产生的偏移角这个问题上,引力对于线速度的影响也是极其微小的,因此Soldner在分析中仅考虑引力产生的方向改变而忽略引力对线速度的影响也是合理的。
【[1]】戴榕菁(2024) 广义相对论之对与错 【[2]】戴榕菁(2024)还Soldner一个公道 [[3]] Dai, R. (2024). What Is Wrong and Right with General Relativity. Retrieved from: https://www.academia.edu/120069979/What_Is_Wrong_and_Right_with_General_Relativity [[4]]Soldner, J.G.v. (1801–1804). On the deflection of a light ray from its rectilinear motion, by the attraction of a celestial body at which it nearly passes by. Berliner Astronomisches Jahrbuch: 161–172. Retrieved from https://en.wikisource.org/?curid=755966 [[5]]Smethurst, B. (2019). [YouTube] The History of the Speed of Light Part I. URL: https://www.youtube.com/watch?v=V7PU1WN9jWY&t=91s
|
