戴榕菁 1.简单背景 在生活中人们对于物体的这样两种运动已经习以为常:1)物体在压力或撞击力或抛掷力作用下获得初始动量而向上运动然后再由于重力的作用而下落;2)滑轮一侧的链条在向下的拉力作用下借助滑轮的杠杆作用将滑轮另一侧的链条及捆绑在链条上的物体拉向上方。 但是,以英国科普网红史蒂夫莫德命名的莫德效应即著名的链珠喷泉(Chain Fountain)现象【[1]】却向世人展示了与上述经验常识相悖的情景:链条的一侧受到重力作用而下落的运动没有经过任何滑轮的杠杆作用,直接将链条的另一侧往上拉向空中;不仅如此,对于上升侧的链条来说,从被拉动开始上升到超出容器口继续上升的整个过程是连续的,并不存在人们所熟悉的向上抛掷或撞击的瞬间突发作用力,而且如本人在2022年分析指出的【[2]】:上升侧的链条内的拉力是越往上越大。这显然与由于地下压力而喷向空中的自然喷泉的原理完全相悖,因而如我在上文“莫德律与机会欲望”【[3]】中指出的,“链珠喷泉”这个名字具有误导性而且迄今为止主流学界对于该现象的困惑和迷茫在很大程度上恐怕与该名字的误导有关。 相应地,我认为所谓的莫德效应不应被称为链珠喷泉(Chain Fountain)现象,而应被称为“无形的动力滑轮现象”或Invisible Dynamic Pulley Phenomenon简称IDP现象。 2. 莫德效应之最大作用(Action) 对前文“莫德律与机会欲望”【3】之内容的讨论让我对于莫德效应即IDP现象或所谓的链珠喷泉现象突发这样的感慨:这种现象明显违背了自17世纪以来逐渐发展起来的经典力学中的最小作用原理(Principle of Least Action)。 2.1. 最小作用原理 所谓的最小作用原理的基本表达式是一个变分求极值的表达式: δS = 0 (1) 其中的S便是所谓的作用(action)或者也可以说是作用(action)的积分(或求和)【[4]】。经过了由皮埃尔·路易·莫佩尔蒂(Pierre Louis Maupertuis), 莱昂哈德·欧拉(Leonhard Euler),约瑟夫·路易·拉格朗日(Joseph-Louis Lagrange),以及威廉·罗文·哈密尔顿(William Rowan Hamilton)的发展,(1)式可以表达成: 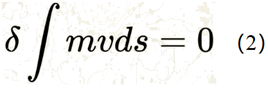
和 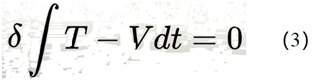
其中mv是动量,T是动能,V是势能。 上面(2)式被称作莫佩尔蒂(Maupertuis)最小作用原理,其中的作用是对路径的积分,(3)式被称为哈米尔顿(Hamilton)最小作用原理,其中的作用是对时间的积分。 莫佩尔蒂最小作用原理成立的条件是总能量不变而哈米尔顿最小作用原理成立的条件是总时间不变;莫佩尔蒂最小作用原理和哈米尔顿最小作用原理的共同前提条件是起点和终点位置不变。 最小作用原理被当作了20世纪物理学尤其是量子理论的基础(尽管这是一个逻辑上有严重缺陷的基础【[5],[6],[7],[8]】)。鉴于变分方程(1)式既可以用来作为极小值的条件也可以用来作为极大值的条件,后来人们进一步发现由(1)式得出的运动学方程既可以代表最小作用的路径也可以代表鞍点(即最大与最小的结合点)作用路径【[9],[10]】,因此将最小作用原理又改称为驻定作用原理(Principle of Stationary Action)。 但是,莫德效应所反映出来的却是作用(action)在某种意义上之最大的路径。 2.2.最大作用之涵义 最小作用原理的变分意义指的是在特定条件下(总能量不变或总时间不变),运动系统将选择所有可能的作用路径中最小的一个。很显然,在现实中这种最小作用的路径的意义是合理而明确的,毕竟不论是按照莫佩尔蒂的方式还是按照哈密尔顿的方式来表达作用(action),只要一个系统发生了运动,它的总作用就不可能是0,所以求它的非零最小值是有意义的;但是,如果按照上述选择最小作用路径的思路来选最大作用路径就有问题了,毕竟在得知最终的运动学解之前,运动系统的作用可以是没有上限的,因而也就无法论及最大值。所以,我们这里需要首先明确本文所说的最大作用的意义是什么。 2.2.1.作用(action)的物理意义 尽管最小作用原理已被20世纪物理学界当作了物理学最最基本的原理,但是主流物理学界在过去的几百年里却一直没有对作用(action)的物理意义给出过明确的诠释。甚至最早提出作用(action)概念的莫佩尔蒂(Maupertuis)还因自己说不清别人也不承认作用(action)有实际的物理意义而在他人的嘲弄声中悲伤离世【4】。 大约一年前(2024),经过对于作用(action)的实际意义进行深入的形而上的分析,本博客指出【[11],[12]】作用的实际意义是自然界运动所涉及的三个基本要素(时间,空间距离,作用力)之间的乘积之和(或积分),或者说是由时间,空间距离,和作用力构成的抽象空间的长方体的体积之和;相应地,所谓最小作用原理就是由时间,空间距离,和作用力构成的抽象长方体的体积之和取最小值。这里插一句,这里的抽象长方体的体积之和的最小值其实意味在正确的路径的每一小段上的作用(action)都取最小值。 2.2.2. 莫德效应之最大作用路径 在明确了所谓的作用的物理意义实际上是时间,空间距离,及作用力三者之积的和之后,我们就比较容易来了解莫德效应之最大作用的意义了。我们不难注意到在莫德效应发生的过程中链条是逐渐上升至一个最大高度然后再下降;而在这整个过程中的任意一个时间点上,链条都在不间断地从容器中被拉向空中然后跨过那个无形的滑轮再顺着重力的牵引下落。由此不难看出莫德效应之最大作用路径的意义。 首先,链条整体高度增大的上升本身就伴随着作用(action)的增大这一点应该不难理解。比如,你从三十层楼丢一东西下来所经历的作用(action)一定是大于你从三层楼丢一东西下来所经历的作用(action)。。。。因此,莫德效应一定不满足最小作用原理! 其次,链条上升能达到一个最大高度然后下降这一点本身就意味着莫德效应实实在在地对应着一个具有“最大”意义的作用(action)值,也就是说其作用值不是可以任意增大的。当然,如前面提到的莫佩尔蒂最小作用原理和哈密尔顿最小作用原理都是说作用(action)在特定的条件下取最小值一样,莫德效应的作用(action)取最大值也是有条件的。。。。目前我们已知的能够产生莫德效应的条件包括:需要是金属珠子的链条而不是小金属环的链条也不是轻塑料的珠子的链条,链条在容器中有足够的深度以便产生足够的阻力,容器离地足够高。。。。这些听起来很不深刻,但遗憾的是这就是目前人们对于产生莫德效应所需的条件的了解。。。。尽管我相信这背后一定有更一般和深刻的力学原理,但在有人去做更加系统和全面的实验研究之前,我们也很难再对于莫德效应产生的条件做出更一般和更深刻的描述了。。。。 3. 最慢无序化过程 其实,除了前面提到的莫佩尔蒂(Maupertuis)和哈米尔顿(Hamilton)的最小作用原理各自所需的前提条件之外,经典力学中的所谓最小作用原理最基本的前提条件就是对于简单系统(如单个粒子或简单刚体运动等)在理想环境下(如真空或稀薄空气中)的运动的分析。对于现实世界的复杂环境中的运动来说,最小作用原理不成立的例子随处可见。 比如,一块具有相当面积(面积与重量之比较大)的平板从无风的高空落下时通常所经历的不是竖直下落而是水平飘落。与竖直下落相比,水平飘落所受的阻力一定更大,下落时间也一定更长(甚至所经历的路径都可能因为横向移动而更长,不过路径的增长在这里不是重点),因此根据我前面给出的作用(action)的意义我们很容易判断出,高空飘落的平板一定不是选择最小作用的路径。。。。当然,与莫德效应相比,高空飘落的平板之所以不采用最小作用的路径比较容易有直觉的解释:假如平板竖直下落,那么它的下端所受阻力会大于上端所受阻力,因此只要稍微偏离完全竖直的位置,就会受到一个令其转向水平的力矩。。。。而当平板处于水平位置时,它的状态就相对稳定。一个与之相关且大家比较熟悉的例子是一个没有经过训练的人从高空跳水的话,他大概率地会横着拍向水面而不是向训练有素的运动员那样竖直地如水。。。。这里的区别在于,对于没有经过训练的素人来说,自然替他选择路径,而训练有素的运动员则由他的大脑控制肌肉来抵御自然的操控。 经典力学中人们经过计算也发现平板水平飘落虽然不满足最小作用原理,但满足最小熵增原理。 对于莫德效应来说,定义它的熵增就过于抽象了。不过,莫德效应与平板下落运动之间有一个共同的特点,那就是它们选择的都是最慢无序化的过程,或者说它们都选择尽可能多地保持有序化状态的运动途径。 4. 结束语 人类对于自然的认识是一个不断深化和纠错的过程。自十多年前人们发现了被称为莫德效应的现象后,主流学界将之命名为链珠喷泉现象(Chain Fountain)并至今一直受到这个名字的心理暗示误导而试图找出该现象背后可以与自然界的喷泉原理类似的原理。但是,自然界在这里给轻视哲学思维的主流学界开了个玩笑。如我自2022年开始指出的,莫德效应的作用原理不是自下而上的推力,而是自上而下的拉力;因此,该现象在作用原理上与自然界的喷泉并无共同之处,反而更象是链条的一侧在重力作用下通过一个“无形的滑轮”将链条的另一侧拉向空中,所以被称作“无形的动力滑轮现象”更为贴切。。。。这种现象在物理理论上的重要性在于它提供了一个在比较理想的环境(比如,可以是真空)里严重违背最小作用原理(Principle of Least Action)的实例,从而让人们对于被20世纪物理学界当作物理学最最基本的所谓的最小作用原理的局限性能有更好的了解。。。。。。 另,本文最初的题目为“最大作用实例?”。。。经过一番斟酌决定改为“莫德效应之最大作用意义”。
[[1]]Chain Fountain, Wikipedia, Retrieved from: https://en.wikipedia.org/wiki/Chain_fountain. Last edited on 3 January 2025, at 01:36 (UTC). [[2]]Dai, R. (2022). The Dynamics of the Chain Fountain. Global Journal of Science Frontier Research: A Physics and Space Science Volume 22 Issue 8 Version 1.0 Year 2022 Type: Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Online ISSN: 2249-4626 & Print ISSN: 0975-5896. pp. 1-6. Retrieved from: https://globaljournals.org/GJSFR_Volume22/E-Journal_GJSFR_(A)_Vol_22_Issue_8.pdf 【[3]】戴榕菁(2025)莫德律与机会欲望 [[4]] Muller, D. (2024). [YouTube] Is The Universe Just An Optimization Machine? [video] url: https://www.youtube.com/watch?v=Q10_srZ-pbs 【[5]】戴榕菁(2024)薛定谔方程与量子化 【[6]】戴榕菁(2024)探秘薛定谔方程的推导 [[7]]Dai, R. (2024). A Short Survey of the Defects in Schrödinger’s Derivation. Retrieved from: https://www.researchgate.net/publication/383751232_A_Short_Survey_of_the_Defects_in_Schrodinger's_Derivation [[8]] Dai, R. (2024). Schrödinger Equation and Quantization. Retrieved from: https://www.researchgate.net/publication/385379588_Schrodinger_Equation_and_Quantization [[9]]Wikipedia. Action principles. Retrieved from: https://en.wikipedia.org/wiki/Action_principles. Last edited on 26 November 2024, at 16:21 (UTC). [[10]]Gray, C. G. and Taylor, Edwin F. (2007). “When action is not least”. American Journal of Physics. 75 (5): 434–458. Bibcode:2007AmJPh..75..434G. doi:10.1119/1.2710480. ISSN 0002-9505. Retrieved from: https://www.eftaylor.com/pub/Gray&TaylorAJP.pdf 【[11]】戴榕菁(2024) 没有说清楚的作用 [[12]]Dai, R. (2024). The Meaning of Action. Retrieved from: https://www.researchgate.net/publication/378519243_The_Meaning_of_Action 
|
