戴榕菁 1.基本概念 受到被称为化学之父的波义耳(Robert Boyle 1627-1691)在十七世纪发明的自流瓶(Self-flowing flask)的启发,本文在这里推出多层虹吸低耗发电塔(Multifloor Siphoning Powewr Tower, i.e. MSPT)的设想。 图1是一个关于多层虹吸低耗发电塔的示意草图。这个示意图的底部是一个大的蓄液池(或蓄水 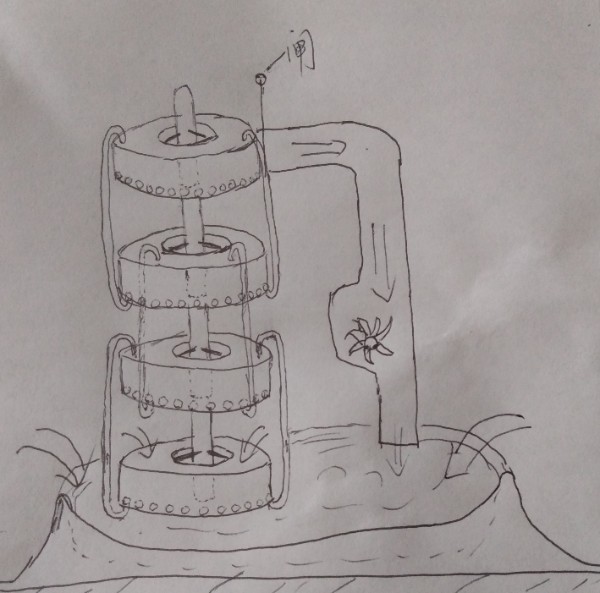
图1多层虹吸低耗发电塔示意草图 池),池中的左侧建有由中心梁柱连接的数层小蓄液池。尽管图中只画出最基本的四层,在实际建构中可以是高达数百米的几十层,甚至更高。每相邻两层之间有数百(甚至更多)根虹吸管从下面一层将液体引入上面一层。在最顶层处有一个由闸门控制的出口与右侧的向下导流的通道相连,通道接近底部大池处装有水力发电机,由高处落下的液柱击打发电机转子叶片产生电能。 2.基本原理和要素 这里的基本原理是流体力学中的伯努利原理:P +(1/2)ρv2+ρgh=constant 其中ρ是流体密度,v是速度,g是重力加速度,h是高度,P是压强。 要素1)每一层的“小”水池的横截面直径要远大于该层的所有的虹吸管的管径之和,这样当液体的粘度和密度合适时,在虹吸作用下就可以将下一层中的水注入到上一层的池中,如此接力一直到最高一层的池中; 要素2)中间层次所起到的只是接力的作用。我们的最终目的是将底部大池中的液体以所要求的速度源源不断地输入到具有所期待的高度的顶层的蓄液体池中。因此,多层虹吸低耗发电塔的最主要的设计指标之一便是顶层的高度;从这一点来考虑,我们似乎应该尽量拉大层与层之间的距离,这样可以减少建筑与运行成本。但另一方面,在液体与空气的密度比给定的前提下,每一层的水压所能产生的虹吸作用又受到虹吸管高度的限制,这就使得层与层之间的距离不能太大。当多层虹吸低耗发电塔的高度达到一定程度后,或许需要考虑大气压力随高度的变化,但是在几百米以内的高度下,可以忽略大气压随高度的变化; 要素3)多层虹吸低耗发电塔的第二个主要的设计指标是顶层的蓄液量,当其横截面积给定时其蓄液量就取决于池子的深度。 要素 4)多层虹吸低耗发电塔的另一个主要的设计指标是其排水的速度。当顶层的蓄水量给定后,其排水能力又取决于下面各层的虹吸喷流的速度,而虹吸喷流的速度又与各层本身的深度有关。一个简单的设计是让所有层的深度与面积都相等。这样便于计算和管理。 要素5)多层虹吸低耗发电塔的每层上的每一根虹吸管的入口处都要装有开关,由中央统一控制; 要素6)多层虹吸低耗发电塔的整体结构,包括底部大液池在内都应该建在室内,一方面可以减少液体挥发,另一方面便于控制空气和液体的物体参数; 要素7)为了防止因中间环节的堵塞而产生溢流,每层的最大设计蓄液深度应在一个小于池子本身深度的安全范围内。
要素8)为了减少粘性摩擦损耗,所有的虹吸管内壁都涂有与所用液体相斥的涂料(如果液体为水的话,就用疏水涂料)。 3.基本能耗 1)预启动能耗 虽然多层虹吸低耗发电塔的工作原理是通过虹吸将底部的液体引入顶层,但是为了缩短启动时间提高启动效率,有必要在启动前将各层都注入最大设计蓄液量。这将是多层虹吸低耗发电塔的一大能耗; 2)初始动量能耗 初始动量对于多层虹吸低耗发电塔的成功运转有着决定性的重要作用。很多试图否认波义耳的自流瓶的可行性的人给出的最主要的误导性的理由便是试图用流体静力学来解释其运作机理。而波义耳自流瓶能正常运作的基本条件却如上所述是流体力学的伯努利方程所表达的动力过程。因此,初始动量起着至关重要的作用。 为了产生足够的初始动量,我们可以采取如下两个措施: (1)在启动前的注液过程中,关闭所有的虹吸管的入口处的开关。在启动的瞬间同时打开所有的虹吸管的开关。这样可以产生一个瞬间的冲量。 (2)当所有的虹吸管的开关都瞬间被打开后,每一层的蓄液量都会有所下降,这时如果下面的虹吸流由于某种原因而未能及时达到,那么不但会影响上面的流动的稳定性,甚至会造成某一层的虹吸的失败。一旦某一层的虹吸失败后,就不容易再马上产生突然打开开关的那种冲力效果,而要将该层的开关关闭,将虹吸管中液体除去,重新启动,这时其上面各层即便是已经有了成功的虹吸现象,也会因为没有后继的流体补充而失去持续虹吸的动力。 因此,为了避免由于一些偶然的因素(比如管道没清干净等)导致虹吸失败,在打开虹吸管的开关之后,各层应仍然有一段时间保持由外面向池内注入液体。 这是多层虹吸低耗发电塔的另一个主要的能耗。 3)正常运转能耗 由于塔顶泻下的液体直接流入底部的大池子中,因此,需要有动力持续地将液体从大池子中输入到最底层的小池中以维持其中的蓄液量。 4)其它能耗 以上三项是多层虹吸低耗发电塔的最主要的能耗,除此之外,多层虹吸低耗发电塔自然还需要照明取暖控制室内环境等等各种基本的能耗。 在上述的能耗中,第1项和第2项都是在启动时的一次性能耗。一旦多层虹吸低耗发电塔开始正常运行后,便可停止。第4项是所有机构都必须的日常能耗,与多层虹吸低耗发电塔的运作没有直接的关系。只有第3项才是多层虹吸低耗发电塔的正常能耗。可见,多层虹吸低耗发电塔利用虹吸原理以用来补充一层蓄液量的极低的能耗将液体引入到几十米甚至几百米的高度。 4.能量来源 对于那些对“永动机”的概念极为过敏的人来说,他们最为关心的问题将是多层虹吸低耗发电塔的设计是否会因为违背了能量守恒而无法实现。这里就解释一下多层虹吸低耗发电塔的能量来源: 多层虹吸低耗发电塔主要有两个能量来源,其一是大家一眼就看出的重力势能,而其二则是大气压力所作的功。因此,多层虹吸低耗发电塔只能在地球或有类似的大气压的环境下运作,而无法在月球上运作。 5.一点讨论 根据网上一些视频中的显示,虹吸作用最大可以将液体提升到容器中深度的三倍左右。当然,虹吸的高度不能仅由相对值来判断,因为它存在着一个绝对的上限。这一点可以从前面的伯努利方程看出。由于在前面的伯努利方程中的三项之和为固定的,假如我们忽略容器表面较小的速度,并将其高度设为零,那么整个流动的总能量就是由该处的压力决定,而该处的压力为气体静压力,也就是一个大气压。所以,虹吸管内的流体的速度项与高度项之和一定是有极限的,小于一个大气压减去流体内的压力。而在这两项中,流体的速度越小,它的高度越大。 这样就产生这么一个问题:即便我们能够通过虹吸作用以提升一米或几米的能量将液体提升几十米或数百米的话,如果到达最顶层的速度很慢,那么也无法满足高速发电的要求。这一点虽然是一个很大的挑战,却不是致命的问题。这是因为虹吸的引水量是由容器的面积与虹吸管的面积之和决定的。因此,如果到达最顶层的速度较慢,我们可以通过扩大蓄水池的总面积来弥补。 6. 多层虹吸低耗发电塔的优势 (1)与核电相比的优势 多层虹吸低耗发电塔发电不存在让很多人闻之色变的核电事故的风险,更没有令所有具有核电的国家都头疼的核废料的处理问题; (2)与火力发电相比 多层虹吸低耗发电塔发电不存在因为燃烧而产生污染及高排碳的问题; (3)与地热和其它绿能发电相比 多层虹吸低耗发电塔发电对自然条件要求低。只要有一块合适的空地,就可以用来进行多层虹吸低耗发电塔发电。 (4)与一般的水力发电相比 除了在上面第3点中提到的对自然条件要求低这一优势之外,我们还可以通过对多层虹吸低耗发电塔发电所使用的液体进行化学处理而提高其效率,这是用天然的水资源发电无法做到的。另外,用多层虹吸低耗发电塔发电还可减少因对于天然水资源的干扰而对自然生态的破坏或对水资源的污染。 7.结束语 鉴于上述这些优势,我相信,在本博客过去这些年里提出的(包括用地球技术制造飞碟在内的)所有工程技术的构想中,多层虹吸低耗发电塔是最有希望在短时期内引起人们的重视并得到实际应用的。而本文对于人类在未来对多层虹吸低耗发电塔技术的应用的最大贡献是使得未来任何一个国家和公司都因为本文的提前公布而无法用多层虹吸低耗发电塔技术概念来申请专利,因此多层虹吸低耗发电塔技术将成为造福全人类的廉价清洁能源。当然,相信未来的使用者们还会在具体的技术细节上申请各种专利;所以,本文的另一个效果将是引发有关多层虹吸低耗发电塔技术的开发热情,毕竟谁先开发,谁将拥有专利的优势。
|
