续上文:闲侃 (4):以圆锥曲线的眼光看狭义相对论
那里,俺们介绍了三种不同形式的时空变换,包括大家所熟知的加利略变换 (Case a)) 和络仑兹变换 (Case b)),然后介绍了第三种形式的“络仑兹变换”:Case c)。文章结尾部分,俺们说了,将要考察这三种时空变换对应的几何模型。
先说说那篇文章的一个错误,对应 Case c) 的。Case c) 对应的时空变换公式仍然有效,但是应该去掉那里提到的适用范围约束:那里俺说了Case c) 对应有个最小速度的物理世界。这里,“最小速度”这个限制应该去掉,那个变换和加利略变换一样,适应于所有的速度。络伦兹变换之所以速度不能超过 1,是因为平方根的要求。这样一来,上文最后两个图中的几条直线 (红色 and 蓝色) 也就没啥意义了,是多余的。文章闲侃 (4) 也懒得修改,因为那不影响大局;而且,保留这种 traceable/trackable 的 mistakes,也挺有意思的。这里,我们将上文闲侃 (4) 中的 statements a)、b)、c) 改成:
在看起来非常合理的假设下,从变换群的观点出发,可以推理出咱们这个物理世界的时空变换必须对应以下三种情形之一:
a) 速度可以是任意值;时间是绝对的,时空的变换是抛物型的;
b) 速度存在个上限值;时空的变换是双曲型的;
c) 速度可以是任意值;时空的变换是椭圆型的。
我们来考查三种时空变换的几何结构。通常,不同的平面几何有不同的分类系统,比较常见的一种分类系统是根据长度和角度的测量方法分类。长度的测量可以分为椭圆的、抛物的、双曲的等三种类型,角度的测量也类似,也可以分为椭圆的、抛物的、双曲的等三种类型,所以整个平面几何就能分为九种不同类型的平面几何,见下表 (可以参见苏联学者雅格龙的著作,九种平面几何):
角度测量分类
|
长度测量分类
|
椭圆型
|
抛物型
|
双曲型
|
椭圆型
|
椭圆几何学
|
欧几里得几何学
|
双曲几何学
|
抛物型
|
伴欧几里得几何学
|
加利略几何学
|
伴闵可夫斯基几何学
|
双曲型
|
伴双曲几何学
|
闵可夫斯基几何学
|
二重双曲几何学
|
对绝大部分读者而言,除了熟悉“欧几里得几何”以外,其余的八种非欧几何,恐怕都不会熟悉。就几何结构而言,其实是加利略几何学最简单,其次是欧几里得几何学和闵可夫斯基几何学。这里,对 Case a)、b)、c) 而言,其对应的长度测量都属于“抛物型”的 (具体什么意思,因为篇幅的缘故,就不解释了),但是就角度测量而言,它们是完全不同的。
历史上最早出现的几种非欧几何:罗巴切夫斯基几何 & 黎曼几何,就是上表中的双曲几何和椭圆几何。注意这里的“黎曼几何”和广义相对论的数学工具“黎曼几何”不是同一回事情。黎曼是高斯的学生,他们师徒都是人类历史上最有才华、成就最卓绝的几位数学家之一。历史上唯一能和他们师徒相提并论的,恐怕只有欧几里得和阿基米德师徒。
熟悉群论的读者很容易验证,咱们所说的三种时空变换都各自形成一个连续群 (李群),分别称为迦利略变换群、洛伦兹变换群,以及 Case c) 所对应的变换群。从几何角度而言,每个时空变换对应着一次坐标旋转 (因为群元的矩阵表示已经 normalized 成 1)。我们先从 Case c) 看起,因为从转动意义而言,它反而是大家最熟悉的。我们暂且称 Case c) 对应的变换为椭圆型络仑兹变换 (暂时的名称,以后有可能随时改掉,呵呵)。
Case c) 椭圆型络仑兹变换。考虑二维时空,我们有如下的变换:
t1 = b * ( t + v*x)
x1 = b * (-v*t + x)
或者写成矩阵形式:
(t1, x1)' = A (t, x)',A_11 = b,A_12 = bv,A_21 = -bv,A_22 = b,这里 b = 1/sqrt (1+v^2),v 是速度,可以取任意值,包括 0。如前所说,椭圆型络仑兹变换保持二维时空的“距离” s^2 = t^2 + x^2 不变。 下次闲侃俺若不码别的内容,就会试图导出“椭圆型络仑兹变换”(Case c)) 所对应的 10 个生成元之间的代数结构,顺便再考虑“椭圆型络仑兹变换”和物理中假想的快子 (Tachyon) 之间有没有联系,i.e. 看“椭圆型络仑兹变换”能否描述快子 Tachyon 的运动。
若定义角度 w 使得 cos w = b,那么很容易验证 sin w = bv,so we have
A_11 = cos w, A_12 = sin w,
A_21 = -sin w, A_22 = cos w。
而且,
A(w1)*A(w2) = A(w1+w2)
例如 A(w1)*A(w2)_11 = cos w1*cos w2 - sin w1*sin w2 = cos (w1+w2),这和二维欧几里得空间的转动是一样的,这就表明椭圆型络仑兹变换对应的平面几何关于角度的测量是椭圆型的,因此它对应的几何恰好是欧几里得几何。见下图中的第一个图。
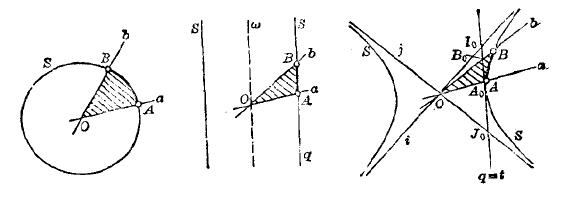
(欧几里得几何、加利略几何、闵可夫斯基几何的单位圆和角度示意图。
角度就是阴影部分的面积。横座标表示时间 t,纵座标是空间 x)
Case a) 迦利略变换,我们有如下的变换:
t1 = t
x1 = x - vt
或者写成矩阵形式:
(t1, x1)' = A (t, x)',
A_11 =1, A_12 = 0,
A_21 = -v, A_22 = 1,
v 是速度,可以是任意值,包括 0 和无穷大。如前所说,迦利略变换保持时间 t 不变,和 x 完全无关。很容易验证:
A(v1)*A(v2) = A(v1+v2)
见上图中的第二个图 (并且和第一个图对比),这时,第一个图中的单位圆就退化成一根直线 t = 1,亦即迦利略变换下的不变量 t 取单位长度 (第一个图中的单位圆就是椭圆型络仑兹变换下的不变量 t^2 + x^2 = 1,对不对),因此它对应的平面几何恰好是加利略几何。
Case b) 络仑兹变换。(rescale 使得最大速度 -- 光速 = 1):
t1 = a*( t - v*x)
x1 = a*(-v*t + x)
这里 a = 1/sqrt(1-v^2),就是所谓的洛伦兹因子。因为 v < 1,所以 a > 1,无须赘述。写成矩阵形式:
(t1, x1)' = A (t, x)',
A_11 = a, A_12 = -av,
A_21 = -av, A_22 = a
如前所说,络仑兹变换保持二维时空的“距离” s^2 = t^2 - x^2 不变。和上图第一个图对应的“单位圆”,就是双曲线 t^2 - x^2 = 1。
若定义双曲函数的双曲角度 w 使得 cosh w = a,那么 sinh w = av。对某些忘记了双曲函数的读者而言,我们这里温习如下:
sinh x = (e^x - e^(-x)) / 2; cosh x = (e^x + e^(-x)) / 2; tanh x = sinh x/cosh x;
利用恒等式(cosh x)^2 - (sinh x)^2 = 1,很容易验证:
A_11 = cosh w, A_12 = -sinh w,
A_21 = -sinh w, A_22 = cosh w
而且,A(w1)*A(w2) = A(w1+w2),这和二维双曲面上的转动是一样的,这就表明络仑兹变换对应的平面几何关于角度的测量是双曲型的,因此它对应的几何恰好是闵可夫斯基几何。见上图中的第三个图。
对三种时空变换而言,其对应的动力学变换群 (作为李群) 都有十个生成元:三个直线运动 (boost) 对应三个生成元 (也就是不考虑动力学内容时上述变换群本身的生成元),时间方向对应一个生成元 (哈密顿量),三个空间方向的动量对应三个生成元,空间方向的三个转动 (角动量) 对应三个生成元。自然,生成元之间的对易关系 (李代数结构) 是不一样的,其中以加利略变换群的李代数结构最为简单。加利略变换群和络仑兹变换群的李代数结构都可以在教科书上查到。
|
