1963-1964年，在长期供职于欧洲核子中心（CERN）後，约翰·贝尔有机会到美国斯坦福大学访问一年。北加州田园式的风光，四季宜人的气候，附近农庄的葡萄美酒，离得不远的黄金海滩，加之斯坦福大学既宁静深沉，又宽松开放的学术气氛。这美好的一切，孕育了贝尔的灵感，启发了他对EPR佯谬及隐变量理论的深刻思考。

贝尔开始认真考察量子力学能否用局域的隐变量理论来解释。贝尔认为，量子论表面上获得了成功，但其理论基础仍然可能是片面的，如同瞎子摸象，管中窥豹，没有看到更全面、更深层的东西。在量子论的地下深处，可能有一个隐身人在作怪∶那就是隐变量。

根据爱因斯坦的想法，在EPR论文中提到的，从一个大粒子分裂成的两个粒子的自旋状态，虽然看起来是随机的，但却可能是在两粒子分离的那一刻（或是之前）就决定好了的。打个比喻说，如同两个同卵双胞胎，他们的基因情况早就决定了，无论後来他（她）们相距多远，总在某些特定的情形下，会作出一些惊人相似的选择，使人误认为他们有第六感，能超距离地心灵相通。但是实际上，是有一串遗传指令隐藏在它们的基因中，暗地里指挥着他们的行动，一旦我们找出了这些指令，双胞胎的‘心灵感应’就不再神秘，不再需要用所谓‘非局域’的超距作用来解释了。

尽管粒子自旋是个很深奥的量子力学概念，并无经典对应物，但粗略地说，我们可以用三维空间的一段矢量来表示粒子的自旋。比如，对EPR中的纠缠粒子对A和B来说，它们的自旋矢量总是处于相反的方向，如下图中所示的红色矢量和蓝色矢量。这两个红蓝自旋矢量，在三维空间中可以随机地取各种方向，假设这种随机性是来自于某个未知的隐变量L。为简单起见，我们假设L只有八个离散的数值，L=1，2，3，4，5，6，7，8，如下图所示，分别对应于三维空间直角坐标系的八个卦限。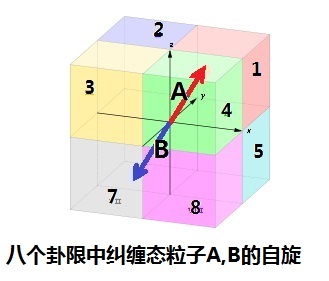

由于A、B的纠缠性，图中的红矢和蓝矢总是应该指向相反的方向，也就是说，红矢方向确定了，蓝矢方向也就确定了。因此，我们只需要考虑A粒子的自旋矢量（红矢）的空间取向就够了。假设红矢出现在八个卦限中的概率分别为n1,n2┅n8。由于红矢的位置在8个卦限中必居其一，因此我们有∶n1+n2+n3+n4+n5+n6+n7+n8 = 1。

现在，我们列出一个表，描述A、B的自旋矢量在3维空间可能出现的8种情况。下图中的左半部分列出了在这些可能情况下，自旋矢量在xyz方向的符号∶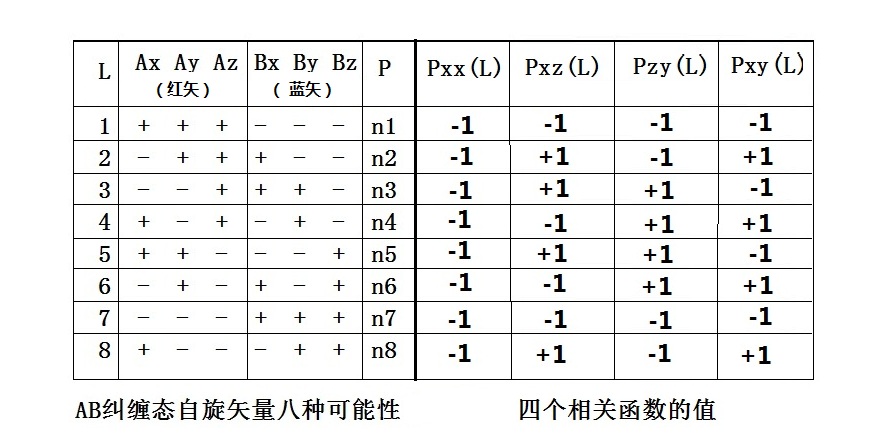

既然AB二粒子系统形成纠缠态，互为关联，我们便定义几个关联函数，用数学语言来更准确地描述这种关联的程度。比如，我们可以如此来定义Pxx(L)∶观察x方向红矢的符号，和x方向蓝矢的符号，如果两个符号相同，函数Pxx(L)的值就为+1，否则，函数Pxx(L)的值就为-1。我们从上表左边列出的红矢蓝矢的符号不难看出，Pxx(L)的8个数值都是-1。然後，我们使用类似的原则，可以定义其他的关联函数。比如说，Pxz(L)，是x方向红矢符号，与z方向蓝矢符号的关联，等等。

在上图中的右半部分，我们列出了Pxx(L)，以及Pxz(L)、Pzy(L)、Pxy(L)的数值。

现在，贝尔继续按照经典的思维方式想下去∶我们的小孙悟空A和B蹦出石头缝时，它们的两个自旋看起来是随机的，但实际上是按照上面的列表互相关联。然後，他们朝相反方向拼命跑。经过了一段时间之後，两个小孙悟空分别被如来佛和观音菩萨抓住了。如来和观音分别对A和B的自旋方向进行测量。因为L是不可知的隐变量，因此，只有关联函数的平均值才有意义。根 上面表中的数值，我们不难预测一下这几个关联函数被测量到的平均值∶

Pxx = -n1-n2-n3-n4-n5-n6-n7-n8 = -1

Pxz = -n1+n2+n3-n4+n5-n6-n7+n8

Pzy = -n1-n2+n3+n4+n5+n6-n7-n8

Pxy = -n1+n2-n3+n4-n5+n6-n7+n8

让我们直观地理解一下，这几个关联函数是什麽意思呢？可以这样来看∶Pxx代表的是A和B都从x方向观测时，它们的符号的平均相关性。因为纠缠的原因，A、B的符号总是相反的，所以同被在x方向观察时，它们的平均相关性是-1，即反相关。类似的，Pxz代表的是从x方向观测A，从z方向观测B时，它们符号的平均相关性。如果自旋在每个方向的概率都一样，即∶n1=n2=┅n8=1/8的话，我们会得到Pxz为0。对Pzy和Pxy，也得到相同的结论。换言之，当概率均等时，如在相同方向测量A、B的自旋，应该反相关；而如果在不同方向测量A和B的自旋，平均来说应该不相关。

我们可以用一个通俗的比喻来加深对上文的理解∶两个双胞胎A和B，出生後从未见过面，互相完全不知对方情况。一天，两人分别来到纽约和北京。假设双胞胎诚实不撒谎。当纽约和北京的警察问他们同样的问题∶“你是哥哥吗？”，如果A回答“是”，B一定是回答“不是”，反之亦然。对这个问题，他们不需要互通消息，回答一定是反相关的，因为问题的答案是出生时就因出生的顺序而决定了的（这可相仿于Pxx=-1的情况）。但是，如果纽约警察问A∶“两人中你更高吗？”，而北京警察问B∶“你跑得更快吗？”，按照我们的经典常识，两人出生後互不相识，从未比较过彼此的高度，也从未一起赛跑。所以，他们的回答就应该不会相关了（这可相仿于Pxz=0的情况）。

现在再回到简单的数学∶我们在Pxz、Pzy和Pxy的表达式上，做点小运算。首先，将Pxz和Pzy相减再取绝对值後，可以得到∶

|Pxz-Pzy| = 2|n2-n4-n6+n8| = 2|(n2+n8)-(n4+n6)|                  （1）

然後，利用有关绝对值的不等式|x-y|<=|x|+|y|，我们有∶

2|(n2+n8)-(n4+n6)| <= 2(n2+n4+n6+n8) =

(n1+n2+n3+n4+n5+n6+n7+n8)+(-n1+n2-n3+n4-n5+n6-n7+n8) = 1+Pxy      （2）

这样，从（1）和（2），我们得到一个不等式∶

|Pxz-Pzy|<= 1+Pxy                                                （3）

这就是著名的贝尔不等式。上述不等式是贝尔应用经典概率的思维方法得出的结论。因此，它可以说是在经典的框架下，这三个关联函数之间要满足的约束条件。也就是说，经典的孙悟空不可以胡作非为，它的行动是被师傅唐僧的紧箍咒制约了的，得满足贝尔不等式！

但是，如果是量子世界的量子孙悟空，情况又将如何呢？当然只有两种情形∶如果量子孙悟空也遵循贝尔不等式，那就好了，万事大吉！爱因斯坦的预言实现了。量子论应该是满足‘局域实在论’的，量子孙悟空表现诡异一些，只不过是因为有某些我们不知道的隐变量而已，那不着急，将来我们总能挖掘出这些隐变量的。第二种情况∶那就是量子孙悟空不遵循贝尔不等式，贝尔用他的‘贝尔定理’来表述这种情形∶“任何局域隐变量理论都不可能重现量子力学的全部统计性预言”。如果是这样的话，世界好像有点乱套！

不过没关系，贝尔说，重要的是，这几个关联函数是在实验室中可能测量到的物理量。这样，我的不等式就为判定EPR和量子力学谁对谁错提供了一个实验验证的方法。

那好，理论物理学家们说，我们就暂时停止耍嘴皮，让将来的实验结果来说话吧。

上一篇∶帮倒忙的贝尔

下一篇∶纠缠态及实验