| 第二章∶简单分形 “王二不简单啊!”张三说∶“你看,数学上真的有如你所说的分数维┅┅” 王二却假装丧气地说了一句笑话∶“唉,可惜我晚生了100多年,要不然,我就是第一个提出分数维的人了┅┅” 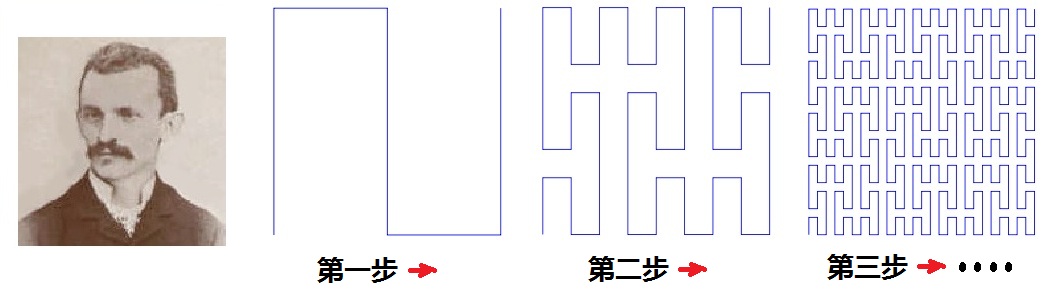 图(2.1)∶皮亚诺和他的space filling curve 原来非整数维的需要,早在1890年,就被意大利数学家皮亚诺(G.Peano)提出。他当时构造了一种奇怪的曲线。你们看,按照图(2.1)的方法一直构造下去,最後所逼近的极限曲线,应该能够通过正方形内的所有的点,充满整个正方形。那不就等于是说∶这条曲线最终就是整个正方形,就应该有面积!这个结论令当时的数学界大吃一惊。一年後,大数学家希尔伯特也构造了一种性质相同的曲线。这类曲线的奇特性质令数学界不安∶如此一来,曲线与平面该如何区分?对这种奇怪的几何图形,当时的经典几何似乎显得无能为力,不知道该把它们算作什厶。 这类奇怪的曲线,包括我们在上一章中介绍过的分形龙,都是分形的特例,不同的迭代方法,可以形成各种各样不同的分形。自皮亚诺之後,科学家们对分形的研究,形成了一个新的几何分支,叫做“分形几何”。 分形(Fractal)是一种不同于欧氏几何学中元素的几何图形。简单的分形图,例如上一章中所举的分形龙例子,很容易从迭代法产生。还有许多看起来更简单的分形曲线。比如,如图(2.2)所示的科赫曲线。  图(2.2)科赫曲线的生成方法 尼尔斯·冯·科赫(Niels von Koch) (1870ˉ 1924)是一位瑞典数学家,出生于瑞典一个显赫的贵族家庭。冯·科赫的祖父曾担任瑞典的司法大臣,父亲是瑞典皇家近卫骑兵团的中校。研究数学和哲学,是当年瑞典贵族阶层的流行风尚,如今闻名世界的诺贝尔奖,就是由瑞典皇家科学院专设的评选委员会负责评审和颁发的。冯·科赫在1887年被新成立不久的斯德哥尔摩大学录取,师从著名的函数论专家哥斯塔·米塔格-列夫勒(Gösta Mittag-Leffler)。由于斯德哥尔摩大学当时尚未获得颁发学位的许可,之後他又就读于乌普萨拉大学,在此校获得文学士及哲学博士学位之後,被斯德哥尔摩的皇家工学院任命为数学教授, 在短短的54年生命中,冯·科赫写过多篇关于数论的论文。其中较突出的一个研究成果是他在1901年证明的一个定理,说明了黎曼猜想等价于素数定理的一个条件更强的形式。但是,他留给这个世界的最广为人知的成果,还应该是这个此文中所介绍的以他而命名的科赫曲线。 科赫在他1904年的一篇论文“关于一个可由基本几何方法构造出的,无切线的连续曲线”中,描述了科赫曲线的构造方法。 如图(2.2)所示,科赫曲线可以用如下方法产生∶在一段直线中间,以边长为三分之一的等边三角形的两边,去代替原来直线中间的三分之一,得到(a)。对(a)的每条线段重复上述做法又得到(b),对(b)的每段又重复,如此无穷地继续下去得到的极限曲线就是科赫曲线。科赫曲线显然不同于欧氏几何学中的平滑曲线,它是一种处处是尖点,处处无切线,长度无穷的几何图形。科赫曲线具有无穷长度。这点很容易证明∶在产生科赫曲线的过程中,每一次变换都使得曲线的总长度变成原来长度的三分之四倍,也就是说乘以一个大于一的因子。例如,如果假设开始时的直线段长度为1,在图(2.2a)中,折线总长度为4/3;而(b)图的折线总长度为(4/3)*(4/3);(c)图的折线总长度为(4/3)*(4/3)*(4/3);这样一来,当变换次数趋向于无穷时,曲线的长度也趋向于无穷。 科赫雪花则是以等边三角形三边生成的科赫曲线组成的,如图(2.3)所示。 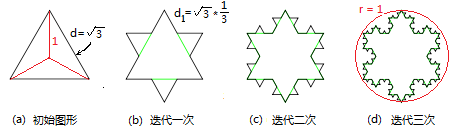 图(2.3)科赫雪花 李四指着图(2.3)说∶“你们看,这科赫曲线处处连续而处处不可微┅┅”话还没说完,就被王二打断了,王二指着(b)中的一段直线∶ “连续是对的,我怎厶看不出处处不可微呢?这些平平的三角形边上直线的部分不都是可微的吗?” 李四明白了王二的困惑之处,笑嘻嘻地解释道∶“问得好!这是一个很重要的概念∶我们用迭代的方法生成分形,但是,生成过程中的那些图都不是分形,只是最後那个无穷迭代下去的最後极限的图形才叫做‘分形’!” 张三说∶ “对,所以实际上,分形是画不出来的。” 王二也明白了∶“是呀,只能看着图,再加上想象┅┅” 言归正传,因为每条科赫曲线都是连续而无处可微的曲线,每条曲线的长度都是无限大,所以,由三条科赫曲线构成的科赫雪花的整个周长也应该是无限大。然而,从图中很容易看出,科赫雪花的面积却应该是有限的。因为整个雪花图形是被限制在一个有限的范围之内。比如,科赫雪花的面积应该是大于图(2.3a)中正三角形的面积 3*1.5,而小于图(2.3d)中红色圆形的面积pi。 利用初等数学很容易求得图(2.3)中,作无限次迭代之後科赫雪花图形的面积。 设A0为初始三角形的面积,An为n次迭代之後图形的面积,读者不难得出下面的迭代公式∶  上一篇∶从分形龙谈起 返回目录 下一篇∶分数维是怎厶回事? |
