第十六章﹕三体问题及趣闻
话说回来,在19世纪初,狭义相对论和量子力学掀起物理学革命的那几年,爱因斯坦正年富力强,精力充沛,而庞加莱却是疾病缠身,心力交瘁。庞加莱又肩负着数学领袖的重任,数学中有太多太多的由他提出、而又尚未证明的猜想和定理,占据了他的大部分时间和精力。想必他也无暇去顾及思考更多有关狭义相对论的问题了。 的确,作为一个数学家,庞加莱一生所系、不断思考、至死念念不忘的,还是数学问题,是由他始开先河的微分方程定性理论研究和代数拓扑学。因此,让我们在本章中,还回到当年的三体问题,以及庞加莱为解决三体问题而发展的数学。这其中蕴涵着庞加莱最重要的创新:把握定性和整体的拓扑思想。 国王奥斯卡二世用以悬赏N体问题的奖金数额不算很多,但全世界的数学家们仍然趋之若鹜,为什麽呢?因为能够获此奖项将是一个莫大的荣誉,再则,所悬赏的N体问题本来就是数学上一个极为重要、有待解答的问题。 二体问题早在牛顿时代已被完满解决,三体问题却至今仍然悬而未决,一直是人们关注的焦点。1878年,美国数学家希尔(1838—1914)发表文章【1】,论证月球近地点运动具有周期性。希尔的工作引起庞加莱对三体问题发生了极大的兴趣。庞加莱本来就一直在研究这个问题,因此,国王的悬赏对他而言,只是正中下怀,来得正是时候。这送上门来的名利双收机会,何乐而不为呢? 根据牛顿的万有引力定律,学过高中物理的学生都不难列出三体问题的运动方程,它是含有九个方程的微分方程组。但是,求解这个方程则是难上加难,并不存在一般条件下的精确解。庞加莱首先采取了希尔的办法,将此问题简化成了所谓‘限制性三体问题’。 限制性三体问题是三体问题的特殊情况。当所讨论的三个天体中﹐有一个天体的质量与其他两个天体的质量相比﹐小到可以忽略时﹐这样的三体问题称为限制性三体问题。首先,我们把小天体的质量m看成无限小﹐就可以不考虑它对两个大天体的作用。这样,两个大天体便按照开普勒定律,绕着它们的质量中心作稳定的椭圆运动(不考虑抛物线和双曲线的情形)。然后,我们再来考虑小天体的质量m有限时,在两个大天体m1和m2的重力场中的运动。也就是说,我们将小天体对大天体的作用忽略不计,只考虑大天体对小天体的吸引力。如此一简化,原来的九个微分方程组变成了只有三个变量的微分方程组。 例如,当初的希尔就是用更简化了的‘平面圆型限制性三体问题’,来研究月球的运动。他略去了太阳轨道偏心率﹑太阳视差和月球轨道倾角﹐得到了月球中间轨道的周期解。如今,航天科学家们常用限制性三体问题,研究在月球、地球引力的作用下,人造卫星、火箭及各种飞行器的运动规律。 即使简化成了三个微分方程,只有三个变量,也仍然无法求出精确解啊。庞加莱意识到,要解决问题必须想出新的办法,总不能在一棵树上吊死。既然无法求出精确解,就放弃寻找精确解的努力好啦!于是,庞加莱开始定性地研究解的性质。也就是说,从三个微分方程出发,用几何的方法,从整体上设法了解可能存在的各种天体轨道的性质和形态。这样,庞加莱为微分方程定性理论的研究铺平了道路。 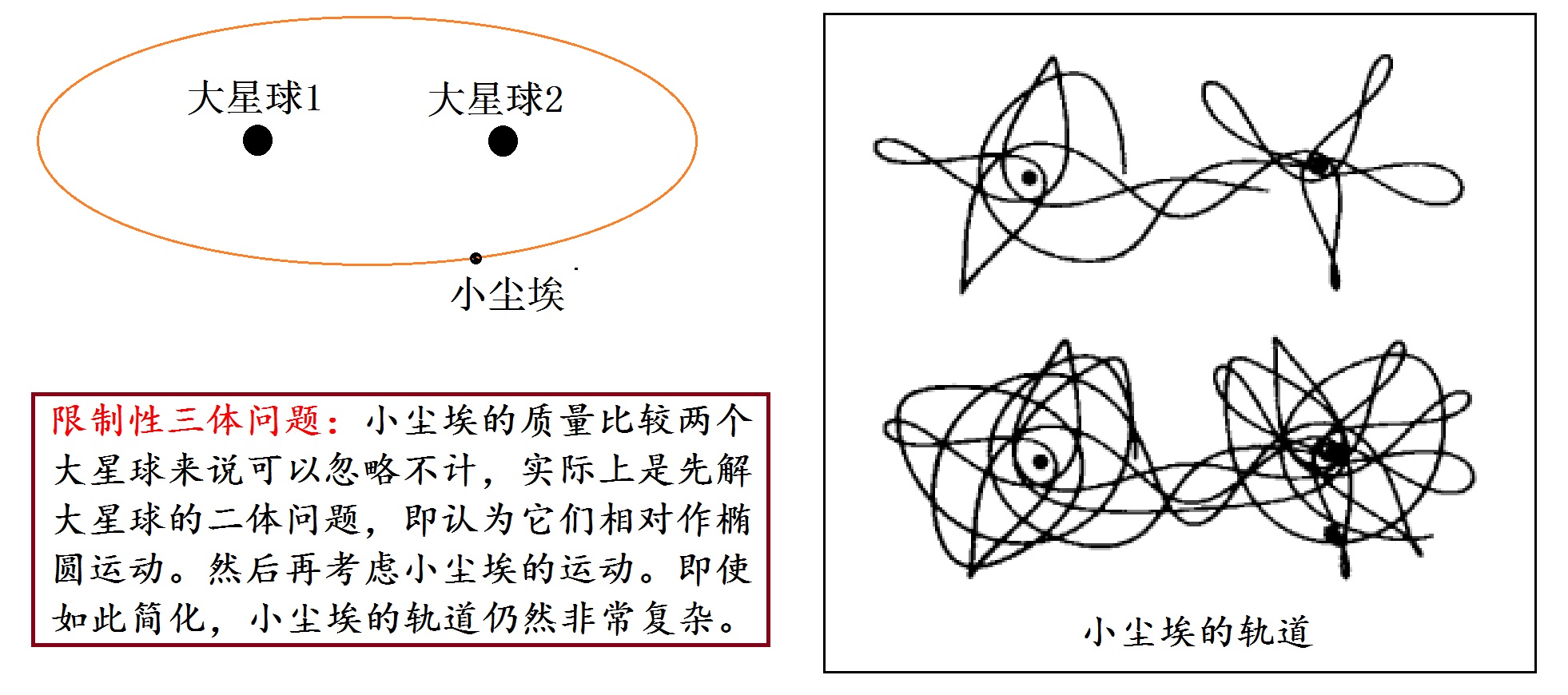
图(16.1)限制性三体问题 如图(16.1)所示,庞加莱企图定性地研究包括小尘埃和两个大星球的‘限制性三体问题’。这种情形下,两个大星球的二体问题可以精确求解,大星球1和2相对作椭圆运动。庞加莱需要定性描述的只是小尘埃在大星球1和大星球2的重力吸引下的运动轨迹。 庞加莱运用渐近展开与积分不变性的方法,定性研究小尘埃的轨道。他深入研究小尘埃在所谓‘同宿轨道’和‘异宿轨道’(相当于奇点)附近的行为,但一直没有得到令他满意的结果,最后不得不在1888年五月,比赛截至之前提交了他的论文。国王悬赏的评审团成员是当时三位鼎鼎有名的数学家:法国数学家Charles Hermite(Hermitian矩阵以他命名),德国数学家卡尔·魏尔斯特拉斯及他的学生:瑞典数学家米塔-列夫勒。尽管庞加莱并没有完全满足奥斯卡二世悬赏的要求,没有解决N体问题,但他的160页的文章仍然令评审团的三位数学巨匠兴奋无比。他们认为庞加莱对三体问题的研究取得了重大突破,太阳系的相对稳定得到确认。维尔斯特拉斯在给米塔-列夫勒的信中写道:“请告诉您的国王,这个工作不能真正视为对所求的问题的完善解答,但是它的重要性使得它的出版将标志着天体力学的一个新时代的诞生。因此,陛下预期的公开竞赛的目的,可以认为已经达到了。” 于是,国王高兴地把奥斯卡奖—2500瑞典克朗和一枚金质奖章,授予了庞加莱。 在1889年冬天,评审团准备将庞加莱的论文在数学杂志上发表。文章已经印好,而且送到了当时最有名的一些数学家那里。就在这时,负责校对的一位年轻数学家发现文章中有一些地方的证明不够清楚,建议庞加莱增加一段解释作为补充材料。于是,庞加莱开始重新深入研究这一部分。 庞加莱越是深入研究小尘埃的轨道在奇点附近的性质形态,发现的问题就越多。情况有些类似八十多年后MIT的气象学家洛伦茨面对的困境。当然,他不如洛伦茨幸运, 能在计算机的屏幕上显示奇异吸引子的曲线。但是,庞加莱却以他惊人的思维和想象能力, 在自己的头脑里构造出了‘限制性三体问题’的某些奇特解的雏形。从解的奇怪行为中,庞加莱看到了当今人们所说的‘混沌现象’。不过, 局限于他当时的经典世界观,他还未能完全理解得到的结果, 只能迷惑而感叹地说了一句:“无法画出来的图形的复杂性令我震惊!”(见图(16.1)右图) 既然解的图形复杂得无法画出来,庞加莱意识到,在原来的论文中,不仅仅是像那个年轻人所说的那种“证明不太清楚”的小问题,而是包含着一个‘错误’。于是,他赶快通知米塔-列夫勒,收回已经印出的杂志予以销毁。同时,庞加莱大刀阔斧地修改和赶写论文。一直到第二年,1890年的十月,庞加莱的长达270页论文的新版本才重新问世。 庞加莱坚持自己支付了印刷第一版的费用:3585克郎,这个数目大大超过了一年之前他得到的奖金。作为题外话,还有一件遗憾之事:几年前有报道说,有人从庞加莱的孙子家里,偷走了当初庞加莱赢得的那枚金质奖章。所以,对这次悬赏活动,庞加莱是倒赔了1000多克郎,金质奖章也不翼而飞。当然,对数学大师而言,区区金钱算什么呢?庞加莱庆幸对论文作了这个重要的修正。并且,正是这个‘错误’,使得庞加莱对方程的解的状况重新研究和思考,改正了他的一个稳定性定理,最终导致了他对同宿交错网的发现。 庞加莱发现,即使对简化了的‘限制性三体问题’,在同宿轨道或者异宿轨道附近,解的形态会非常复杂,以至于对于给定的初始条件,几乎是没有办法预测当时间趋于无穷时,这个轨道的最终命运。而这种对于轨道的长时间行为的不确定性,这也就是我们现在称之为混沌的现象。(图16.2)  图(16.2)限制性三体问题:初值有微小差别的十条轨道随时间的演化过程 点击图像可到JAVA演示程序 http://alecjacobson.com/programs/three-body-chaos/ 参考文献: 【1】G. W. HILL, Researches in the lunar theory, Amer. J. Math. I (1878), 5-26, 129-147, 245-260.
上一篇∶超越時代的龐加萊 返回目录 下一篇∶混沌遊戲
|
