| 第二十章﹕混沌魔鬼‘不稳定’ 王二正在总结他的演讲,谈到他计划中的毕业论文课题: “你们知道,我们这个由各类生物群体组成的大千世界,盘根错节、繁杂纷纭;天下万物,互相制约、互相依存;自然界中形形色色的动植物不停地出生、繁殖、变化、死亡,时而大浪淘沙、优胜劣汰;时而又相辅相成、维持平衡。在永不间断的争争斗斗、生生死死中, 各种生物群体的数目变化莫测,有时侯表现一定程度的周期性, 有时侯又貌似一片混沌,的确有些类似于上两章中所研究的逻辑斯蒂方程的解的行为。我正在想,用逻辑斯蒂方程为基础,是否可能找出一个描述包括多种生物竞争,群体数如何变化的生态模型来……” 王二的想法引起了好几个生物相关专业学生的兴趣,他们聚在一起开始热烈讨论生态学的问题。 其实,逻辑斯蒂方程不仅在生态研究方面意义重大,在别的领域也有诸多应用。是啊,逻辑斯蒂映射看起来太简单了,只有1个变量,1个方程,却能表现出混沌系统的种种特征。还记得我们曾经讨论过的其它混沌系统,比如洛伦茨系统和三体问题吗?相对于它们的原始问题来说,最后的方程也算够简单了,但是,仍然有三个变量、三个微分方程。 混沌理论的老祖宗庞加莱曾经提出一个定理,稍后被瑞典数学家本迪克松证明,说的是混沌现象只能出现在三维以上的连续系统中。但这个定理不适用于离散系统,逻辑斯蒂迭代方程所描述的就是一个特别简单的1维离散系统。混沌魔鬼在这个简单系统中轻巧地跳出来,成为混沌研究者们的最爱。 李四对此深有体会,因为他正在做一个与流体力学、湍流等有关的课题,涉及的系统很复杂。当系统维数太多想不清楚时,李四就总是回到最简单的一维逻辑斯蒂方程,用图形的方法来考虑问题,感觉容易多了。不过,张三今天却说: “总的来说,1个变量的确比3个变量简单很多。不过,有时候,3维的图像也挺直观的。比如说你看,当我用计算机画奇异吸引子的时候,画出来的洛伦茨吸引子多漂亮!洛伦茨方程的解,是随时间变化而无限绕下去、却又永不重复的轨道,在三维空间中画出来,好像一只翩翩起舞、展翅欲飞的蝴蝶。可是,这个逻辑斯蒂方程的吸引子,用图形表示就不好看了。” 张三的说法不无道理。对逻辑斯蒂方程来说,每个不同的k值都有一个吸引子,在‘平衡’区域,吸引子是1个固定点;在‘双态平衡’区域,吸引子是2个固定点;在‘多态平衡’区域,吸引子是多个分离的固定点;而在‘混沌’区域,吸引子是连成一片的点;最后的状态在这些点无规律地蹦来蹦去,到底是如何蹦的?分岔图上对具体过程显示得并不清楚。不过,我们可以用如图(20.1)所示的逻辑斯蒂迭代图,清楚地看到在不同k值下,迭代过程中xn的收敛情形。 图(20.1)中,标为红色的是迭代的最后过程。图中的抛物线对应于逻辑斯蒂方程右边的非线性迭代函数(xn+1 = kxn·(1-xn))。 从左向右看:第一个小图中的xn最后收敛于一个红点;第二个小图中的xn最后收敛于一个红色矩形,标志着有两个不同的x值;而第三个小图中的xn最后收敛的红色区域,是在4个不同的x值中循环;最右边的‘混沌’情况,大家一看圈来圈去的红色曲线便明白了:有点类似于洛伦茨的蝴蝶图了,这是魔鬼现身的表现! 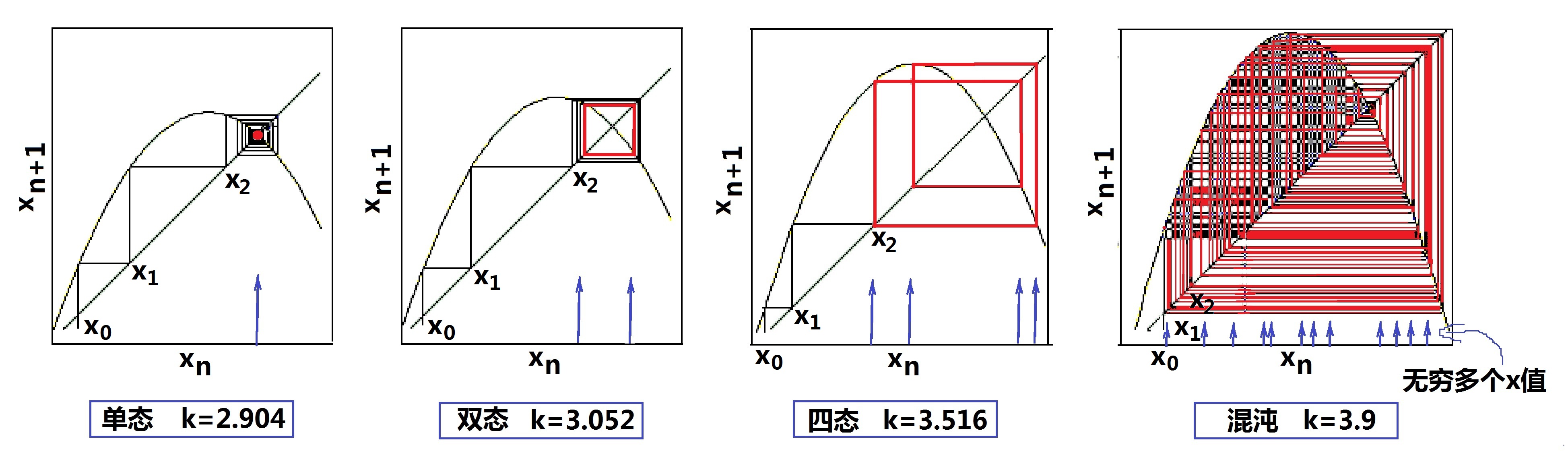 图(20.1):不同k值下的逻辑斯蒂迭代图 逻辑斯蒂系统还有一个少有的优点:它所对应的微分方程可以求得精确的解析解。而大多数非线性系统是无法得出精确解的,只能用迭代法来研究数值解的定性性质,以及解的稳定性。 混沌魔鬼的出现,与参数k的数值有关,k越大,魔鬼出现的几率就越大。这其中有何奥秘呢?我们回到逻辑斯蒂方程描述的生态学,回忆一下参数k的意义是什么?k是群体数的线性增长率,与出生率有关。想到这点,我们恍然大悟:如果k比较大,群体繁殖得太多了,数目增长太快,增加社会不稳定的因素,当然就容易造成混乱,令魔鬼现身啰。 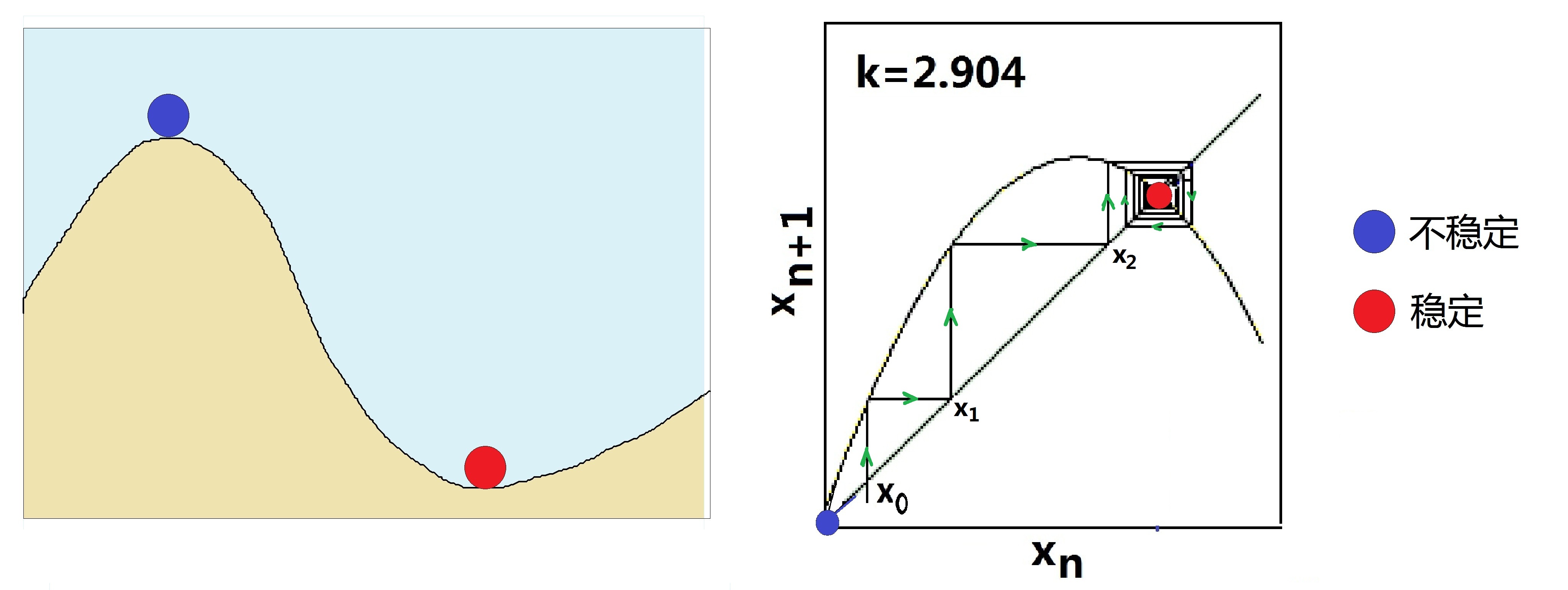
图(20.2):不稳定和稳定 混沌的产生的确与方程的‘稳定性’有关,因此,我们有必要讨论讨论系统状态的稳定性。哪种状态是稳定的?哪种状态是不稳定的?从图(20.2)的左图中一目了然,那是在重力场中‘稳定’和‘不稳定’的概念:对小圆球来说,坡顶和坡谷都是重力场中可能的平衡状态。但是人人都知道,位于顶点的蓝色球不稳定,位于谷底的红色球很稳定。究其根源,是因为只要蓝色球开始时被放斜了那么一丁点儿,就会因不能平衡而掉下去。而红球呢,则不在乎这点起始小误差,它总能够滚到谷底而平衡。用稍微科学一点的语言来说,稳定就是对初值变化不敏感,不稳定就是对初值变化太敏感。我们将这个意思发挥扩展到逻辑斯蒂方程上,考虑图(20.2)的右图中k=2.9时,即吸引子是一个固定点的情况。这时,逻辑斯蒂方程的解应该是图中的抛物线和45度直线的交点,图中的这两条线有两个交点。因此,除了固定吸引子x无穷=0.66之外,x无穷=0也是一个解。但是,在图中所示的条件下,x无穷=0.66是稳定的解,x无穷=0却是不稳定的解。为什么呢?因为只要初始值从0偏离一点点,像图中所画的情况,迭代的最后结果就会一步一步地远离0点,沿着绿色箭头,最终收敛到x无穷=0.66这个稳定的平衡点。 研究三体问题的大数学家庞加莱,是微分方程定性理论的始创者。有关微分方程解的稳定性问题,则由另一位数学家李亚普洛夫始开先河。亚历山大·李亚普洛夫(1857-1918)是与庞加莱同时代的俄国数学家和物理学家。与稳定性密切相关的李亚普洛夫指数,便是以他命名。 如何来判定系统稳定与否?李亚普洛夫想,可以用对重力场中两个小球是否稳定的类似判定方法。于是,他研究当初值变化一点点时,看看系统的最终结果如何变化,并以此来作为稳定性的判据。更具体地说,我们可以将系统的最终结果x无穷表示成初始值x0的函数,用图形画出来。然后,系统的稳定性取决于这个函数图形的走向:它是更接近图(20.3)中的哪一种曲线呢?是向下指数衰减(λ小于0)?还是向上指数增长(λ大于0)?还是平直一条(λ等于0)?第一种情况被认为是稳定的,第二种情况被认为是不稳定的,而λ等于0则是临界状态。这儿的λ便是李亚普洛夫指数。 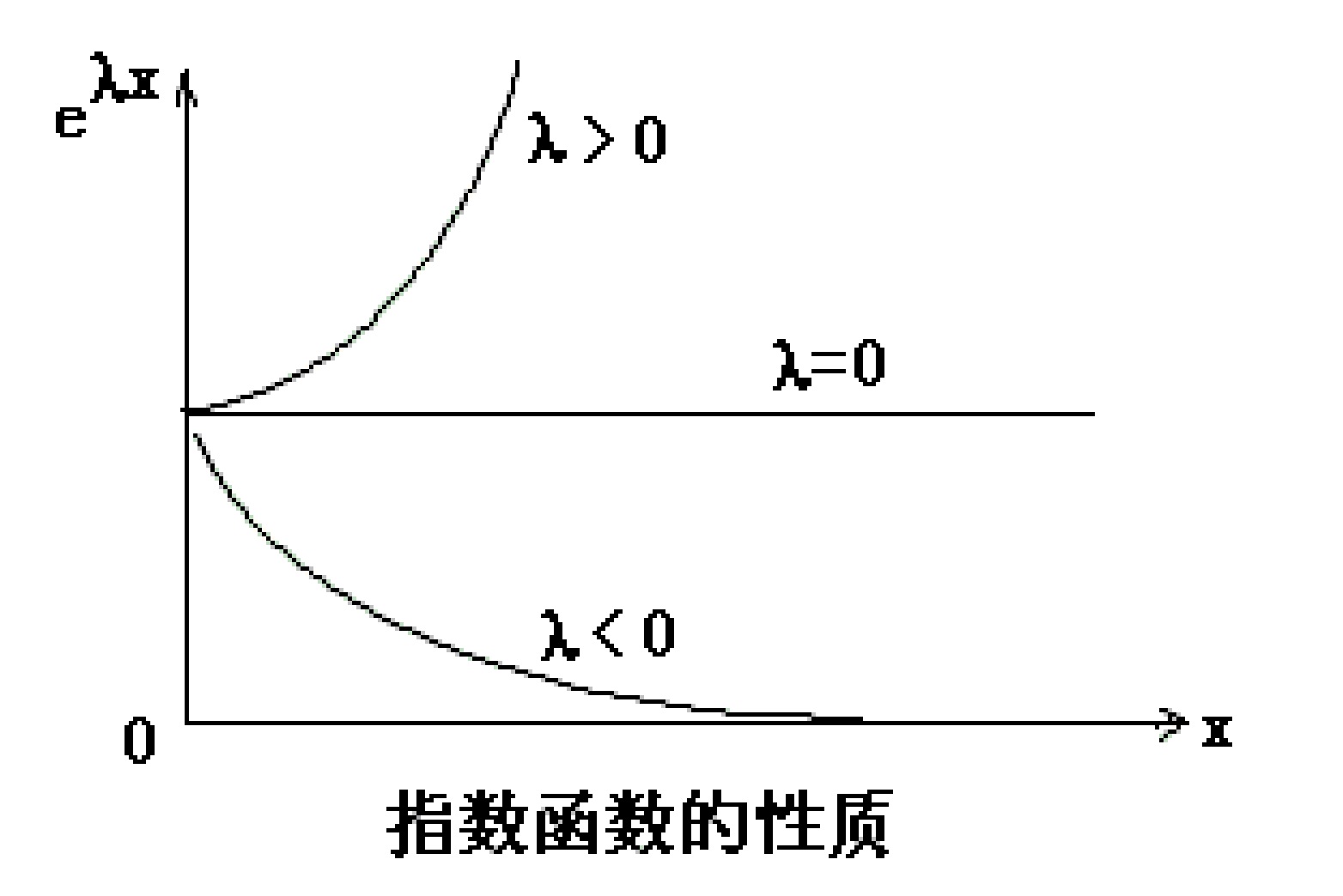
图(20.3):指数函数的性质随λ变化 图(20.4)显示的便是不同k值下,逻辑斯蒂系统的李雅普诺夫指数及对应的分岔图,从中不难看出λ的符号变化与倍周期分岔的产生及混沌魔鬼出现之间的关系:k值比较小的时候,λ小于0,系统处于稳定状态;从k=3.0开始,λ有时等于0,出现分岔现象,系统变到多态平衡,但仍然是稳定的,大多数时候,λ小于0;从k>3.57开始,λ开始大于0,系统不稳定,过渡到混沌。有趣的是,混沌魔鬼露脸后又经常躲藏起来。在λ大于0的区间中,λ的数值还经常返回到小于0的数值。也就是说,混沌有时又变成有序,这对应于分岔图中(黄色图像)中的空白地带。 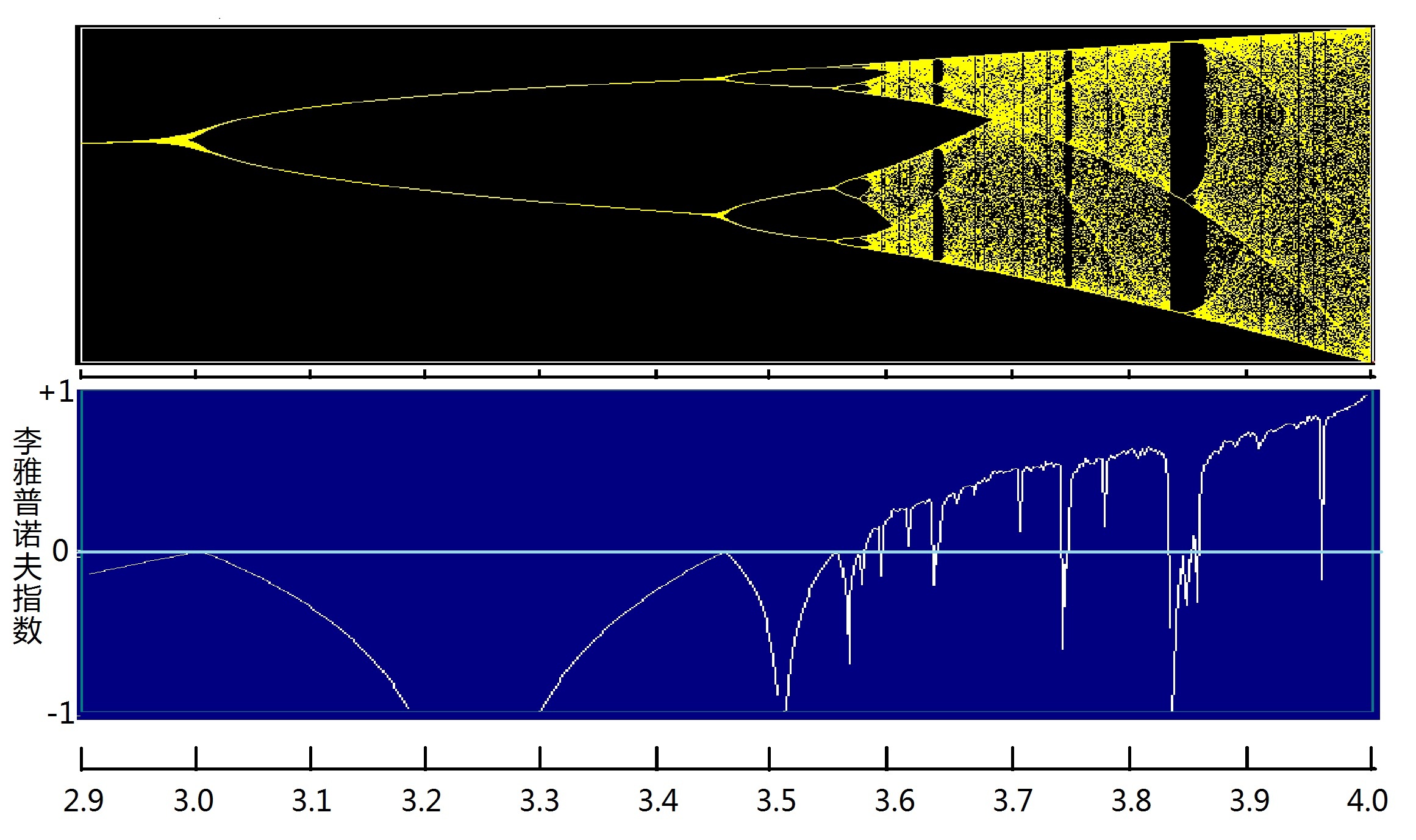
图(20.4):逻辑斯蒂系统的李雅普诺夫指数及对应的分岔情形 上一篇∶有序到無序 返回目录 下一篇∶萬變之不變 |
