前不久俺灌水侃过到底“普通高学历海华”和“高学历普通海华”两种说法到底哪个对(见:闲侃(11):普通高学历海华 vs 高学历普通海华)。其实几乎不用想,前者是对的,后者是不对的。这里我们
construct a
scenario,以一个实例来看为什么后者是不对的。很多时候,语言、文字这种看似和“定量”不搭界的东西其实是可以通过定量半定量的例子加以说明的。
我们先确定两个概念/变量:
a) 教育程度。这个变量 x 假设有7个可能的离散取值:
1) 小学 and 文盲: x = 1;
2) 初中: x = 2;
3) 高中: x = 3;
4) 专科: x = 4;
5) 本科: x = 5;
6) 硕士: x = 6;
7) 博士: x = 7.
当然对学位 x 的赋值只能是大体上的,因为谁也说不清为什么本科 x=5 的话,硕士就对应6,对不对。因此 x 取值 {1,2,3,4,5,6,7} 只能是保证其单调性这个原则下的一种大致近似。
我们再假设具有上述学历的人占据的人数权重分别是 10%,10%,20%,20%,20%,10%,10%。再假设高学历对应于博士学位。而”普通“则对应所讨论群体(收入)50%,亦即中位数附近的老海华。当然我们还有如下的一则implication:
学历和收入是线性正相关的,亦即通常而言,学历越高的人,收入也越高。我们假设这种关联(从统计角度而言)是较强的,但不是很强。
b)收入。记为 y。假设我们将每个学历段的人按照收入分为5个ventiles,分别对应于相应学历段 top 10%,30%,50%,70%和 90% 收入水平的人的收入。我们的 scenario 有如下数值:
学历 | 人数
权重 | 年收入(单位:万) | 名称 | x | Top 10% | Top 30% | Top 50% | Top 70% | Top 90% | 小学 | 1 | 10% | 1 | 1 | 2 | 3 | 4 | 初中 | 2 | 10% | 2 | 3 | 4 | 5 | 6 | 高中 | 3 | 20% | 2 | 4 | 5 | 6 | 7 | 大专 | 4 | 20% | 3 | 4 | 6 | 7 | 9 | 本科 | 5 | 20% | 5 | 6 | 8 | 9 | 11 | 硕士 | 6 | 10% | 7 | 8 | 10 | 12 | 15 | 博士 | 7 | 10% | 9 | 10 | 14 | 18 | 20 | 总计 |
| 100% |
|
|
|
|
|
几位教授(起码,一草,mingcheng99)虽然就“普通高学历老海华”还是“高学历普通老海华”哪个恰当有意见分歧,但根据其文章的意思,应该都是指“博士”那行与收入 50% 那列的交汇点所代表的那类老海华(为醒目起见,我用了红色字体),在我们的 scenario 中这类老海华年收入 14 万。见楼下的 plot 图(注:为了直观显示相应的权重,比如说,一半专科生取值 x=4.另一半以 x=4.25显示出):
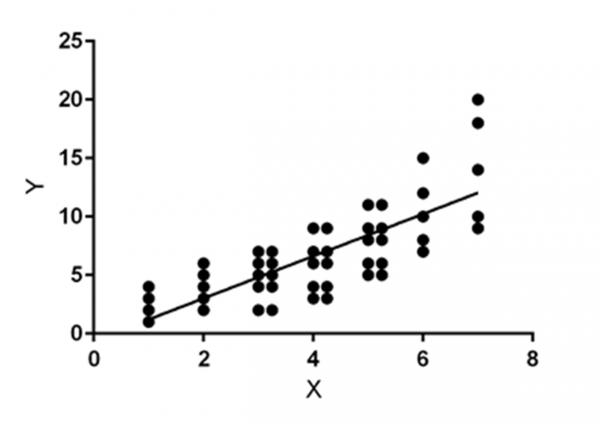
线性回归结果: p < 0.0001,这个值很小了,因此收入和学历是相关的,和打头的 implication 一致。Coefficient of Determination: R^2 = 0.601(因此收入和学历有较强的关联,但不是特别相关)。 “高学历普通老海华”的明确意思以及修饰顺序关系是“高学历(普通(老海华))”,这里“高学历”是修饰“普通老海华”的,而“普通”修饰“老海华”。老海华在这里被我们按照收入和学历分为了50个“等分”,按收入排序如下:
1 1 2 2 2 2 3 3 3 3 4 4 4 4 4 4 5 5 5 5 5 6 6 6 6 6 6 6 7 7 7 7 7 8 8 8 9 9 9 9 9 10 10 11 11 12 14 15 18 20 因此“普通”老海华对应上述第 25、26个数,都是6万,和“高学历”没什么关系。事实上就上述数值而言,第14个数数值是4万,第36个数字是8万,从14-36,几乎占据老海华一半的人口,可还是和“高学历”不搭界。 而“普通高学历老海华”则没有这个问题,因为其修饰顺序关系是“普通(高学历(老海华))”,这里“普通”是修饰“高学历老海华”,而“高学历老海华”对应上述表格中最后一行,“普通”就是指那行5个收入段的中间那个,亦即 14 万所对应的老海华。
很明显,如果收入和学历越相关,即使不考虑汉语语法,“高学历普通老海华”这个说法越不靠谱。在 100% 线性相关的前提下,例如我们假设毛爷爷复生重新掌权,发布行政命令规定临退休的老海华的薪水全国统一定为:
小学:2万;初中:4万;高中:6万;大专:8万;本科:10万;硕士:12万;博士:14万
那么“高学历普通老海华”是 100% 自相矛盾的说法, 这时起码教授的反例证伪就木问题。
|
