| 不过现在,我们可以利用这种‘自相似性’,重新定义几何图形的‘维数’。 仍然利用上面的图,用自相似性来定义的‘维数’可以如此简单而直观地理解:首先将图形按照(N: 1)的比例缩小,然后,如果原来的图形 可以由(M)个缩小之后的图形拼成的话,这个图形的‘维数’d,就等于 ln(M)/ln(N)。不难看出,将上述方法用来分析直线、平面、空间,分别得到d = 1、2、3(上图中的a、b、c)。 上图中的(d),是一种很简单的分形,叫做科和曲线,也是一种自相似图形,它的迭代生成过程如下图所示。 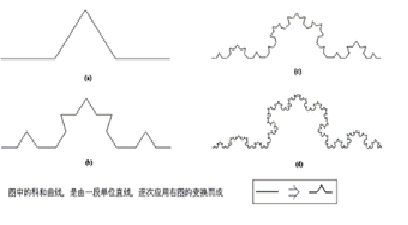 图四 可以用同样的方法分析如图(d)及上图所示的科和曲线:首先,将科和曲线的尺寸缩小至三分之一;然后,用四个这样的‘小科和曲线’,便能构成与原来一模一样的科和曲线。因此,我们得到科和曲线的维数d = ln(4)/ln(3) = 1.2618..。这就说明了,科和曲线的维数不是一个整数,而是一个小数,或分数。 下面,我们再回头研究分形龙的维数(图二)。将图中的分形龙曲线,尺寸缩小为原来的一半之后,得到右上图的小分形龙曲线。然后,将四个小分形龙曲线,分别旋转方向,成为如右下图的位置。最后,再按照右下图中箭头所指的方向,移动四个小分形龙曲线,便拼成了左下图的、与原来曲线一样的分形龙曲线。因此,如此可以证明,分形龙曲线的维数为2,因为(d = ln(4)/ln(2) = 2)。 有趣的是,分形龙图形的边界也是一个可以用迭代法产生的分形: 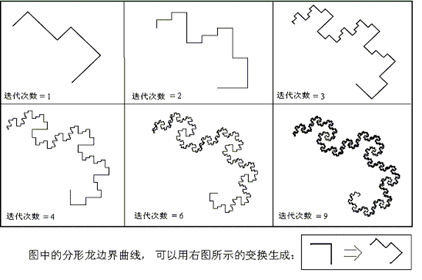 图五 由图六可知,整个分形龙曲线的边界是由四段相似的图形组成的。这种分形的维数估算方法比较复杂一些,它的“分形维数“(d)可以通过解如下方程求得: 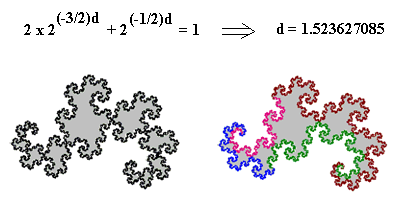 图六 通过分形龙,我们认识了分形,理解了分数维。分形几何是理解混沌概念及非线性动力学的基础,在现代科学技术中,有着广泛的应用。 下面的连接可以让你亲身体会分形龙图形的趣味和美妙: http://www.tianfangyetan.net/cd/java/fractals.html |
