| 一九七零年十月, 美国趣味数学大师马丁·加德纳通过”科学美国人”杂志的”数学游戏”专栏, 介绍给读者一个有趣的数学游戏 - 康维的“生命”游戏。一时吸引了一大批人的兴趣。 生命游戏事实上并不是通常意义上的”游戏”, 它没有游戏玩家各方之间的竞争, 也谈不上输赢,可以把它归类为“仿真游戏”。事实上,也是因为它模拟和显示的图象,看起来颇似生命的出生和繁衍过程而得名为“生命”。游戏在一个类似于围棋棋盘一样的,可以无限延伸的二维方格网中进行。例如,设想每个方格中都可放置一个生命细胞,生命细胞只有两种状态:“生”或“死”。如下图4-1中,用黑色的方格表示该细胞为“生”, 空格表示该细胞为“死” 。游戏开始时, 每个细胞可以随机地(或给定地)被设定为“生”或“死”之一的某个状态, 然后,再根据某种规则(生存定律)计算下一代每个细胞的状态: 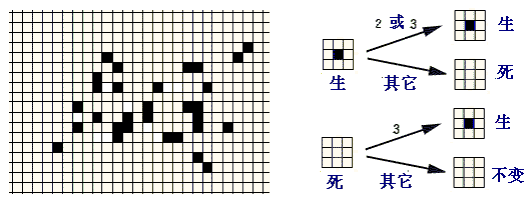 例如,我们可以规定如下的‘生存定律’: 1. 每个细胞的状态由该细胞及周围八个细胞上一次的状态所决定; 2. 如果一个细胞周围有3个细胞为生,则该细胞为生,即该细胞若原先为死,则转为生,若原先为生,则保持不变; 3. 如果一个细胞周围有2个细胞为生,则该细胞的生死状态保持不变; 4. 在其它情况下,该细胞为死,即该细胞若原先为生,则转为死,若原先为死,则保持不变。 然后,同时更新所有的状态,得到第二代的分布图。这样一代一代地作下去,以至无穷。比如说,在下面的图中,从第一代开始,画出了四代细胞分布的变化情况。第一代时,在中心处有四个活细胞,然后,读者可以根据以上所述的四条生存定律,得到第二、三、四代的情况,观察并验证下图的结论。 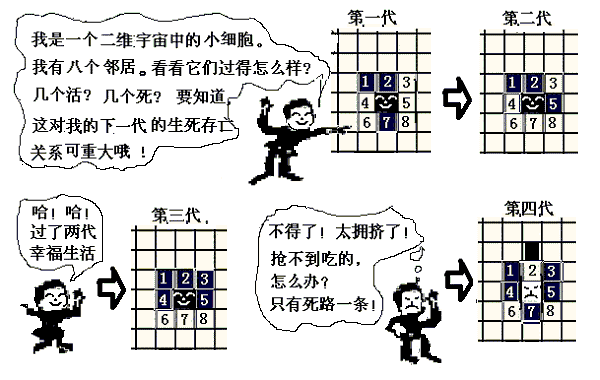
四代二维生命细胞的演化过程
你可能会说,这样的游戏玩起来太不方便了!一格一格地算半天才走一步,也看不出趣味在何处。不过,相信你不会忘记,我们有一个最好的帮手:计算机。我们可以根据四条生存定律编好程序,输入初始状态图,用计算机来进行运算和显示。有了计算机的帮助,就不难发现生命游戏的趣味所在了。例如,如果你选择“随机设置”初始状态,你会看到,游戏开始运行后,迭代过程中细胞生生死死,增增减减,变幻无穷。也许,屏幕上“生命细胞”的图案运动变化的情况,会使你联想到自然界中某种生态系统的变化规律:如果一个生命,其周围的同类过于稀疏,生命太少的话,会由于相互隔绝,失去支持,得不到帮助而死亡;如果其周围的同类太多而过于拥挤时,则也会因为缺少生存空间,且得不到足够的资源而死亡。只有处于合适环境的细胞才会非常活跃,能够自我复制,并进行传播。 我们又一次地悟出这个道理:“复杂的事物(即使生命!),原来也可以来自于几条简单的规律!”。生命游戏为我们提供了一个观察从简单到复杂的好方式。 “生命是如何产生出来的?”,这是一直困惑着我们的大问题。如今这个所谓的“生命游戏”,是否能为解决此问题提供一些有用的线索呢?让我们首先从下面图中所示的,生命游戏中几种特别类型的分布图案说起。 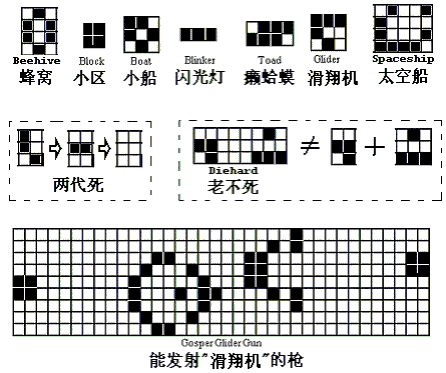 生命游戏中几种特别类型的分布图案 尽管生命游戏中每一个小细胞所遵循的生存规律都是一样的,但由它们所构成的不同形状的图案的演化行为却各不相同。这个现象可以用古希腊哲学家亚里士多德的古老命题“整体大于它的各部分之和” 来表达。不同演化行为的图案大致有如下几种类型:静止型、振动型、运动型、死亡型、不定型。 上面 图中的“蜂窝”,“小区” 和“小船”,都属于静止型的图案,如果没有外界的干扰的话,此类图案一旦出现后,便固定不再变化;而“闪光灯”,“癞蛤蟆”等,是由几种图形在原地反复循环地出现而形成的振动型;图中右上角的“滑翔机”和“太空船”,则可归于运动类,它们会一边变换图形,一边又移动向前。如果你自己用生命游戏的程序随意地试验其它一些简单图案的话,你就会发现:某些图案经过若干代的演化之后,会成为静止、振动、运动中的一种,或者是它们的混合物。 此外,也还有可能得到我们尚未提及的另外两种结果:一类是最终会走向死亡,完全消失的图案;另一类是永远不定变化的情形。就拿“最终死亡”的情况来说吧,“死”的速度可是有快有慢,有的昙花一现,不过几代就断子绝孙了(图中的两代死);有的倒能繁荣昌盛几百上千代:如上图中间的第二个例子就能坚持130代。有趣的是,上例中“老不死”是由两个分图案构成的,这两个分图案如果单独存在,都会长生不死,纠集在一块儿后,尽管也延续了130代,结果却不一样,这又是一个“整体不等于部分之和”的实例。从变幻莫测的生命游戏中,还有许许多多诸如此类的趣事,就无法一一列举了。 叙述至此,应该插入一段历史了。刚才所说的游戏,被称为“康维的生命游戏”,康维,何许人也?为何凭空想出了这生命游戏? 现为美国普林斯顿大学数学教授的约翰·康维,除了致力于群论、数论、纽结理论及编码理论这些多方纯数学领域之外,也是游戏的热心研究者和发明者。在众多贡献之中,他的两个最重要的成果都与游戏有关:一是他在分析研究围棋棋谱时发现了超实数(Surreal Number);其二便是他在英国剑桥大学时发明的生命游戏使他名声大振,特别是经由《科学美国人》连续两期的介绍推广后,康维的名字在70年代的知识界几乎家喻户晓。上世纪的70年代初,使用计算机还只是少数科研人员的专利,对生命游戏中图案演化行为的研究,有些热心者甚至业余时在纸上进行!锯马丁·加德纳后来回忆所述,当时整个国家科研基金的用途中,可能有价值上百万美元的计算机时间,花费于并不十分合法的对“生命”游戏的探索。业余爱好者疯魔于此游戏的规则简单却变化无穷; 生物学家从中看到了”生态平衡”的仿真过程; 物理学家联想到某种似曾相识的统计模型;而计算机科学家们则竞相研究“生命游戏”程序的特点, 最后,终于证明了此游戏与图灵机等价的结论(关于图灵机,以后将有所介绍)。对生命游戏过分的热心和疯狂,大大超出了《科学美国人》的“数学游戏”专栏的负荷能力,以至于当时还专门为此推出了一个名为《生命线》的通讯刊物。 另一件值得一提的趣事是:康维当时还设置了一个五十美元的小奖金,给第一个能证明生命游戏中图形能(或不能)无限制增长的人。这个问题很快就被麻省理工学院的计算机迷Bill Gosper解决了,这就是我们上面图中最下面一个图案“滑翔机枪”的来源。下面的图所示的是滑翔机枪在计算机上运行的图形:一个一个的“滑翔机”永不停止地、绵绵不断地被“枪”发射出来。  这个实例证明了生命游戏中存在无限增长的情形,看起来的确令人鼓舞:由几条简单的“生存定律”构成的“宇宙”中的“枪”,能不断地产生出某种东西,就象机器制造出产品一样。这样一来,是否再进一步,就有可能找到某种图案在演化过程中能自我复制,象生命形成的过程一样呢?如果那样的话,在计算机上模拟生命的复制、进化、突变等现象,似乎已经曙光初现;掌握制造生命的机制,是否也为时不远了呢? 生命游戏程序的连接: http://www.tianfangyetan.net/cd/java/Life.html |
