第十章：简单之美

尽管几个简单的线性自相似的经典分形的历史，最早可追溯到十九世纪後期。但对于分形的深入研究，诸如曼德勃罗图等，却是近四十年的事。这是与计算机的飞速发展分不开的。因为，先进快速的计算技术使得大量的迭代运算可以在更短的时间内完成。图象显示技术的发展为我们提供了探索分形复杂性的方便环境。没有现代的计算机技术，人们不可能欣赏到如此美丽的曼德勃罗图和朱利亚图。

“从艺术的角度，非线性迭代生成的分形图案的确很美。”李四说∶“那种美给我们以视觉的享受，分形音乐则给我们以听觉的享受。但是，科学家们所欣赏的应该是另一种美┅┅”

“对呀！是这个世界所遵循的科学规律的内在之美。”王二抢着补充了几句∶

“你们还记得吧，用计算机生成的树叶图和瞢类植物叶子是如此之相像，还有树枝、脑血管、人体┅┅这段时间我一直在想，世界上这些看起来千变万化的一切，恐怕都是由几条简单的生成规则演化出来的哦，就像张三在计算机程序中用一个简单方程进行迭代一样，细胞分裂又分裂，迭代又迭代，一代又一代┅┅最後就成了我们世界中的各种生物体。啊，不只是生物，还有云彩、闪电、海岸线┅┅几条简单规律产生了大自然的一切┅┅”

看着王二浮想联翩的神态，张三笑了∶“别想象得太远了！想我们力所能及的。你刚才说到的树叶图和厥类植物叶子相像这点，使我想起最近看到的一篇文章，谈到将分形用在计算机图像压缩技术方面的事情。”

计算机技术使得我们能探索分形的复杂性，分形数学又反过来造福于计算机技术。科学和技术总是相辅相成，互相推波助澜。科学始于探索，技术立足于应用。探索能发现自然之美，应用则创造人工之巧。美之事物必能找到应用的途径，而新颖的技术构思又总是能反射出理论的光辉。分形之美与电脑显示技术之新成果息息相关，相照辉映。

当年，分形的研究之所以能在众多的学科范围内引起轰动，其原因之一便是∶如此复杂的结构却产生于几条简单的变换规则。复杂是一种美，简单也是一种美。科学的宗旨之一可以说就是要用简单的规律来描述复杂的大自然。复杂的形态背後可能隐藏着简单的法则。

从分形的这种‘简单表示复杂’的特性，人们很自然地想到了将分形用于作为计算机中储存、压缩图形资料的一种方式。比如象曼德勃罗集那样复杂的图形，只不过是用一个简单的方程（z = z*z + c）就能表示出来。今天，我们的的文明社会正在大阔步地迈进一个数字信息时代。数字化之後的信息需要通过媒介来记录、传送、储存。使用传统的方法储存声音和图像，数 量非常大。因此，我们才有了所谓的图像压缩技术，就是要在保证一定质量的条件下，将储存的信息量减少，减到越少越好。

那厶，有哪些传统的图像储存和压缩方法呢？

在数字世界中，信息量的多少用所需要的比特数（0或1）来衡量。表达信息时所需要的比特数目越小越好。也就是说，最好能将信息“压缩”一下。也叫做给信息“编码”。比如说吧，为了要储存下图中的只有黑白颜色的科赫曲线，我们可以采取如下右边的文字说明中所列举的三种方法编码∶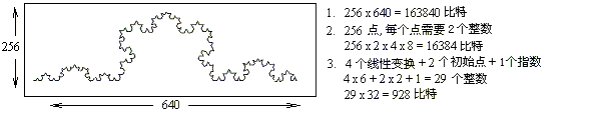

                     图（10.1）∶用不同方法压缩图象的说明

第一种是最原始的方法，是将图形分成许多小格子（象素）。例如，我们可以将图（10.1）分成 256*640个小格子，也就是共163840个象素。然後，需要将这些象素所具有的信息储存起来。因为图（10.1）只是黑白图形，每一个象素的信息不是‘黑’,就是‘白’,正好对应于比特的‘0’或‘1’。这意味着，一个象素需要一个比特来表示。因此，要用这种编码方法储存整个图形，需要的比特数就等于163840。第二种方法是将图形看作诺干点和线。上面的图中共有256条直线，经由256个点逐次连成。所以，只要储存这256个点的位置就可以了。因为每个点在图中的位置需要两个整数表示，而每个整数都需要32个比特来表示。因此，这第二种编码方法需要的比特数是256*2*32=16384。显然，第二种方法比第一种方法更经济合算，因为它将信息压缩了10倍。

如果我们把这个图形用它的分形的初始值及迭代函数来编码的话，就是上图中的第三种方法。使用第三种方法，需要储存的信息只包括4次线性变换迭代以及2个初始点位置。将这些数值换算成比特数，只需要928个比特就可以了。比较原始的163840比特而言，就等于信息被压缩了100倍以上。

有关分形技术用于图像压缩，张三谈起了他自己的经验∶在储存曼德勃罗集图形时，如果存为（BMP）文件的话，文件的大小为430*8千比特，这种方法就相当于上面所说的第一种方法。而如果将它存为（GIF）文件的话，文件的大小仅为30*8千比特。也就是说，在这种情形下，gif格式相对于bmp格式，信息压缩了14.3倍。

张三说∶“可是gif格式也太大了啊，我用程序生成这个图形，存的信息不过是一个简单方程，几个系数，就像刚才的科赫曲线，最多几个千比特，就足够了呀。”

王二又兴奋起来∶“对啦，生物体一定是把某种类似的、最优化的编码存到基因，DNA里面了┅┅大自然往往做得比人工更为精致和巧妙┅┅”

李四却很感兴趣分形图像压缩，说是曾经做过用傅立叶变换压缩声音信号的问题，先和两位一起复习复习。

张三附合∶“对，我们先不管图像信号，声音信号的处理更基本和简单一些。”

其实,不论是声音还是图像信号，最原始的信息都可看作是强度关于时间（或空间）的函数。如我们上面说到的，一个固定的黑白图像可用在每一个像素位置的光强度（0或1）表示，一个原始的声音信息则用在一系列的时间点测量的声音强度来表示。所以，最原始的储存方法就是∶把声音的强度按不同时间点列成一个表储存起来，比如说，转换成电信号保存到磁带上。以後便可以将磁带上的数值读出来，再转换成声音信号。

这种储存声音的原始方法类似于刚才谈到图像编码的第一种方法。可以说是完整的储存方法，但它并不总是最好的，也不是最有效的方法。

声音的信号除了随时间而变的强弱之外，还有一个很重要的特点，就是它的频率。频率也是声波中给我们大脑更深刻印象的东西。学唱歌时首先不就是学“多来米法硕”吗，那描述的就是声音中不同的主频率。

刚说到“多来米法硕”，正好林零和一伙音乐系的女学生在旁边走过，听见这句话便好奇地站下来继续听。

既然频率在声音中是如此重要，人们自然想到储存声音应该储存它的频率。对啦，作曲家们就很聪明，他们将所作的曲子用乐谱的形式记下来，那不就是记录的频率吗？傅立叶变换呢，则是科学家工程师们所使用的乐谱，是由法国数学家在1822年创立的。比之音乐中的乐谱，傅立叶频谱有过之而无不及，它把声音信息中包含的所有频率分量都找了出来。这个过程听起来有点繁琐，似乎画蛇添足！不过，傅立叶变换在数学、物理、工程各方面都得到广泛应用，是信息处理中使用得最多的变换，被誉为信息处理技术上一个重要的里程碑。

储存频谱的优点是储存的信息量少。当我们按下电子琴的中心C按键时，电子琴发出一个‘多’的声音。将这个声音用强度时间表来储存，每1毫秒存一个强度值，1分中就需要存60000个实数，需用3840千比特。如果存它的频谱，暂时不考虑泛音的话，只需要存这个频率的数值和强度，2个实数就可以了，这不就等于是把信息量“压缩”了几千倍吗？即使考虑还得存泛音的数 ，也可以达到几百倍的压缩率吧。

一个女孩有些迷惑不解∶“一个‘多’弹一分钟，这厶长啊？”

大家笑了起来，笑得女孩有些不好意思。可李四说，这个疑问问到了点子上哦！傅立叶变换只记下了频率信号，完全没有时间的信息，是不行的。它就像是用一把频率固定、但时间无限长的尺子来量东西，这把尺太长了！所以，在实际上使用的是如图（10.2）所示的‘窗口傅立叶变换’，把尺子按时间分成一段一段的。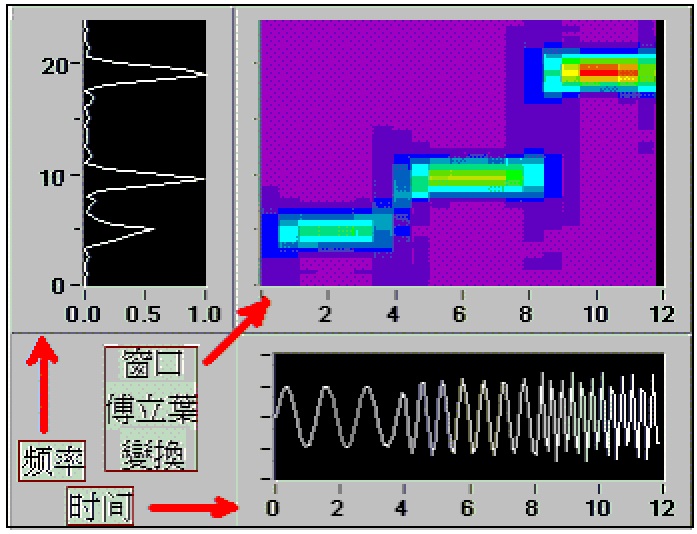

图（10.2）对三段不同频率的正弦函数组成的图形的窗口傅立叶变换结果

林零很有悟性，对王二说∶“这个窗口傅立叶变换的道理和音乐上的曲谱很像啊。既有时间，也有频率┅┅但是┅┅这些和你们谈论的分形又有什厶关系呢？”

王二向她解释了一下刚才谈到的分形用于图像压缩之事。

刚才说到的是对声音信息的傅立叶变换处理。回到图像编码领域，原理也是类似的，只不过需要将时间用二维空间来代替。

对信号的傅立叶变换压缩，利用的是信号的频率特征。用分形的原理进行图像压缩，则是利用图形的自相似性。

分形图象压缩的方法（也称迭代函数系统IFS方法）是美国佐治亚理工学院的巴恩斯利教授首创的。但分形图像压缩技术至今仍然不够成熟。尽管目前已有商品化的计算机软件，但仍有许多问题尚待解决。分形图像压缩的解码速度很快，但编码速度慢，比较 合一次写入、多次读出的文档。

正是∶“路漫漫其修远兮，吾将上下而求索。”