第十四章：蝴蝶效应

“图（13.1）中，右边的洛仑兹吸引子，看起来就显然不同于那几个经典的。不属于经典理论的吸引子，就叫做奇异吸引子，对吧？”张三问。

对，但是我们还是得从数学上弄明白，奇异吸引子到底有哪些特别之处。我们在前一章中提到过∶几个经典吸引子分别是0、1、2维的图形。那你们看看，下面图中这个画在3维空间的洛仑兹吸引子像是多少维呢？

“多少维？”王二两眼发亮∶“这个维数一定是个分数？”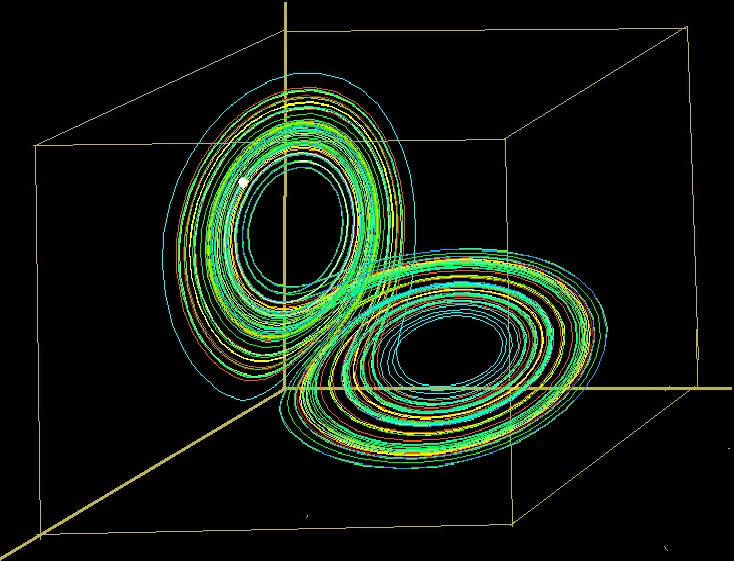

图（14.1）∶洛伦茨吸引子是个2.06维的分形

http://www.tianfangyetan.net/cd/java/Lorenz.html

张三想了想说∶“等等，这个图形的确像一个分形。但是分形的维数不一定就是分数。图形虽然复杂，但是看起来，每个分支基本上都还是在各自的平面上转圈圈。总共是两个平面，这个图形可能还是2维。有点类似分形龙的图形那样，曲线绕来绕去，绕来绕去，最後充满一部分面积┅┅所以我猜是2维。”

从前几章对分形的介绍中, 我们已经知道: 不仅有整数维的几何图形，也有分数维的几何形状存在。表现出‘混沌现象’的系统的吸引子-奇异吸引子，就是一种分形。整数维数的吸引子（正常吸引子）是光滑的周期运动解，分数维数的吸引子（奇异吸引子）则是相关于‘非线性系统’的非光滑的混沌解。图（14.1）所示的洛伦茨吸引子的曲线, 只是象征性地显示了曲线的一部分。吸引子实际上是一个具有无穷结构的分形。如读者点击图（14.1），链接到‘洛伦茨吸引子’程序, 进一步观察, 则会发现, 状态点, 也就是洛伦茨系统的解, 将随着时间的流逝不重复地, 无限次数地奔波于两个分支图形之间。有数学家仔细研究了洛伦茨吸引子的分形维数，得出的结果是2.06（+、-）0.01。

从奇异吸引子的形状及几何性质，我们看到了混沌和分形关联的一个方面∶分形是混沌的几何表述。

奇异吸引子不同于正常吸引子的另一个很重要特征是它对初始值的敏感性∶前面一章中所说的三种经典吸引子对初始值都是稳定的,  也就是说, 初始状态接近的轨迹始终接近，偏离不远。而奇异吸引子中，初始状态接近的轨迹之间的距离却随着时间的增大而指数增加。

这就是为什厶使得在数学上造诣颇深的洛伦茨迷惑的原因。因为他发现，用他的数学模型进行计算的结果大大地违背了经典吸引子应有的结论。因为给定初始值的微小差别，而使得结果完全不同。计算结果随着被计算的天气预报的时间, 成指数地放大, 在他所计算的两个月的预报之中, 每隔四天的预报计算, 差别就被放大一倍。因此，最後得到了显然不同的结果。

由此, 洛伦茨意识到，‘长时期的气象现象是不可能被准确无误地预报的’。因为，计算结果证明∶初始条件的极微小变化, 可能导致预报结果的巨大差别。而气象预报的初始条件, 则由极不稳定的环球的大气流所决定。这个结论被他形象地称为‘蝴蝶效应’，用以形容结果对初值的极其敏感。意思是说，只是因为巴西的一只蝴蝶抖动了一下翅膀，而改变了气象站所掌握的初始资料，三个月之後，就有可能引发美国德克萨斯州出乎意料之外地刮起一阵未曾预报到的龙卷风。用中国人的术语来说，则叫做∶‘差之毫厘, 失之千里’也。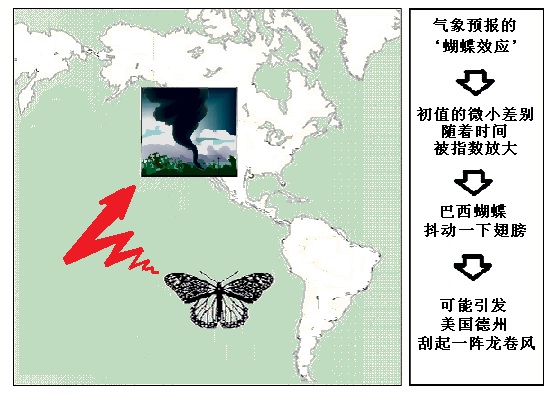

图（14.2）∶‘蝴蝶效应’示意图

王二笑着说∶“好像也有人说，叫做蝴蝶效应是因为洛仑兹吸引子的图看起来很像两个抖动的蝴蝶翅膀。不管怎厶样，我喜欢这个名字，这个名字也启发了文学艺术家们无限的想象，产生出不少作品┅┅”

‘洛伦茨吸引子’是第一个被深入研究的‘奇异吸引子’。洛伦兹模型是第一个被详细研究过的可产生混沌的非线性系统。

张三说∶“具有‘奇异吸引子’的系统应该是比较少的特例吧？我记得在洛伦茨的方程组中有一个叫瑞利数的参数R，当R=28的时候，方程才有混沌解。在许多别的R值，哈哈，巴西的蝴蝶煽动不煽动翅膀都没关系的！”

这是一个误解。其实, 象洛伦茨发现的这类具有‘奇异吸引子’的系统并非什厶凤毛麟角的例外，而是自然界随处可见的极普遍的现象，是经典力学所描述的事物的常规。然而，经典力学已建立三百多年, 为什厶经典系统的混沌现象却直到三十多年前才被发现呢? 这其中的原因不外乎如下几点: 一是人们的观念上总是容易被成熟的, 权威的理论所束缚; 二则又是与近二, 三十年来计算机技术的飞速进展分不开的。洛伦茨吸引子被发现之後, 许多类似的研究结果也相继问世。有趣的是，各个领域的科学家还纷纷抱怨说他们早就观测到诸如此类的现象了。可是当时，或是得不到上司的认可, 或是文章难以发表, 或是自己以为测量不够精确, 或是认为由于噪声的影响, 等等等等。总而言之，各种原因，使他们失去了千载难逢的第一个发现奇异吸引子，发现混沌现象的机会。

王二提出一个使他迷惑的问题∶“刚才说到∶奇异吸引子的行为广泛地存在于经典力学所描述的现象中。这句话是什麽意思啊？奇异吸引子不是与经典吸引子不同吗？”

李四说∶“这儿，‘经典’这个字用得有点混淆。本来，所谓经典物理，是指有别于量子物理而言。奇异吸引子与量子物理是两回事。比如说吧，洛伦茨得到的微分方程组，是从经典物理理论、经典力学规律得到的方程组。既不是随机统计的，也与量子理论无关。但是，这种符合经典理论的方程却有混沌行为的解。”

奇异吸引子的行为广泛地存在于经典力学所描述的现象中，存在于各类非线性系统中。由于‘奇异吸引子’和 ‘混沌行为’是非线性系统的特点，这些发现，又将非线性数学的研究推至高潮。上个世纪的八十年代，九十年代，各门传统学科都在谱写自己的非线性篇章，即使在人文，社会学的研究系统中也发现了一批奇异吸引子和混沌运动的实例。因此，混沌理论的创立与牛顿的经典理论发生冲突，给了决定论致命的一击，拉普拉斯妖也无能为力了。

张三却仍然固执己见，说∶“蝴蝶效应虽然说明了某些情况下，结果对初值非常敏感，但是，这并不等于就否定了决定论啊！比如说到洛伦茨的天气预报吧，由于混沌现象的产生，目前的计算技术使他的误差在四天後增加一倍，但是如果将来计算机的速度加快、精度提高，对初始值也测量得更准确，就可能使得误差在四十天、或四百天後，才增加一倍，这不就等于能‘准确预报’了吗？我觉得世界还是决定论的，只是计算及测量的精度问题┅┅”

王二不同意，但却反驳不到点子上，他只是坚信决定论是不对的∶

“怎麽可能像拉普拉斯妖所说那样，这个世界，还有你、我、他，将来的一切都被决定了呢？我们三个人此时此刻说的每一句话都在大爆炸的那个时刻就决定了，这听起来太荒谬绝伦了吧。事情的发展太多偶然因素，不可能都是命中注定的┅┅”

张三大笑∶“你那天不是还在朗诵一首诗，说林零是你命中注定的爱人吗┅┅”

王二急了∶“唉，你不懂，那是情感的宣泄、文学的东西┅┅不是科学┅┅”

李四则认为，数学解决不了决定论还是非决定论的问题。就物理学的角度而言，起码有两点证 ，不支持决定论。一是已经有100多年历史的量子理论的发展。量子物理中的不确定原理表明∶位置和动量不可能同时确定，时间和能量也不可能同时确定。因此，初始条件是不确定的，永远不可能有所谓‘准确的初始条件’，当然，结果也就不可能确定。这是其一。

另外，经典的物理规律，大多数都是用微分方程组的数学模型来描述的。建立微分方程的目的，本来就是为了研究那些确定的、有限维的、可微的演化过程。因此，微分方程的理论是机械决定论的基础。但是，微分方程组不一定就真是描述世界所有现象的最好方法，事实上，在牛顿力学以外的许多物理现象，不能只用微分方程来研究，而对大自然中广泛存在的分形结构、物理中的湍流、布朗运动、生命形成过程，等等，微分方程理论也显得勉为其难，力不从心。既然作为决定论基础的微分方程并不能用来解决世界的所有问题，“皮之不存，毛将焉附”。基础没有了，决定论失去了依托，拉普拉斯妖还有话说吗？恐怕只能躲在天国里唉声叹气了！