中国古代数学 

古代的东西方皆有早期数学的诞生和发展，可谓彼此独立各有千秋。

1.古中国的算学

古希腊有阿基米德计算球体积的故事，中国的祖冲之和儿子祖暅也得到过同样结果，但晚了约700年左右。不过他们使用的方法，即三国时代的刘徽首先提出、后来被称之为“祖暅原理”的方法，却比西方得到的同样原理（卡瓦列里原理）早了一千多年。

祖暅原理说：“幂势既同，则积不容异”，即如果所有等高处的截面积都相等，二立体的体积必相等。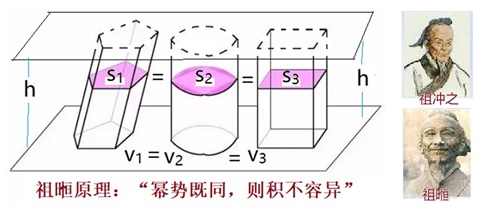

图1：祖暅原理（YouTube视频）

实际上说穿了，中国古代数学的本质就是“计算”。祖冲之是中国古代最伟大的数学家，他的最大贡献就是将圆周率的结果计算到了小数点后第7位，国际上因此称圆周率为“祖率”，并建议将3月14日定为“祖冲之日”。祖冲之的天文成就包括计算和测量回归日及月球绕地周期，其结果与现代数据相差无几，由此月球上一个火山口，被学界命名为“祖冲之火山口”。

古中国与古希腊数学的另一区别是对数学发展的推动力。古希腊人视数学为爱好和游戏，古中国独尊文史轻视数理，因此数学发展的驱动力基本上只是“实用”。“实用是目的，计算为核心”。这也就是为什么有人说中国古代并无“数学”，只有“算学”的原因。

因此，中国古代数学的主要特点是其算学特点。算学也有它先进发达的一面，并非完全没有理论，中国古代数学也有不少密切联系实际的理论，比如与算法相关的推理证明等。中国古代的许多算法，稍加改变可以用到现代的电子计算机上。

古中国数学的机械化思想，与古希腊数学的公理化思想，是数学发展过程中的两套马车，都促进了数学的发展。古希腊以几何为主，古中国多用代数方法，几何比代数更容易公理化，代数比几何更容易发展成机器算法。几何直观形象易于被众人接受，代数在非专业人士眼中则显得枯燥。可以说当时的两者各具优缺点。

古希腊数学衰落而通过阿拉伯传到欧洲的那段时期，正好是中国几位数学家刘徽祖冲之等活跃的时候。这两个分支在各自的跑道上独立发展，没有太大的关联。

在罗马帝国与欧洲中世纪，数学的自由精神受到限制，而中国古代数学却在13世纪（宋朝）时达到了巅峰。

不过再到后来，情况又逐渐走向反面，中国的封建社会和中央集权遏制了学术的发展，学术水平非但不进步反而巨大倒退，文化专制和盲目排外使得数学及科学均逐渐落伍。

2. 韩信点兵--中国剩余定理

“韩信点兵，多多益善”是一个成语，也涉及到中国古代一个著名的数学故事。秦末楚汉相争时，韩信率1500名将士，但第一次战后损伤了3、4百，于是，他急速点兵准备迎接下一场战斗。他的方法与众不同别出心裁。他命令士兵每3人排一排，发现最后多了2名，如每5人排一排则多3名，7人排一排，又是多出2名。然后韩信立即得出了他的兵员数是1073名。

这个数学问题的学术版名字叫做“中国剩余定理”，是我们中国古代数学贡献于世界的最光辉一篇。享誉世界，对数论研究、密码学及通俗如程序设计都有意义。

这道题最早出现在一千多年前的《孙子算经》中。

图2：孙子算经

那只是当时一道不太起眼的叫做“物不知其数”的算术题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”翻译成现在使用的数学语言：一个数除以3余2，除以5余3，除以7余2，求这个数。比较聪明的小学生立刻能凑出来一个数：23。检查一下也的确符合题目所给的3个条件。

我说23是凑出来的，因为23是很小的数！对这个简单情况我们可以使用列举法，

除3余2的数：2，5，8，11，14，17，20，23，26……

除5余3的数：3，8，13，18，23，28……

除7余2的数：9，16，23，30……

满足这三个条件的共同数是“23”，所以便得到了答案。

不过眼尖的读者也发现这个结果并不适合韩信点兵，兵数太少了！韩信的兵至少1000以上啊。不过这个问题有不止一个答案，事实上，答案（通解）可以写成：23+3*5*7*t = 23+105t，其中t = 0, 1, 2……。由此可以得到在任何整数范围问题的答案。例如，如果设t = 10，便得到了韩信的答案。

上面的分析虽然简单，也可以悟出几条此类问题的共同特点：

1，答案需要满足3个条件，2，答案不止一个，可以加上被除数的公倍数的倍数。3，公倍数很重要。

明朝有位数学家叫程大位，他用四句诗概括这个问题的解决方案：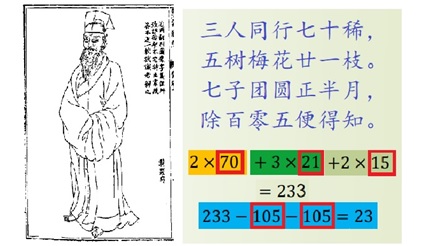

图3：程大位的诗（YouTube视频）

为什么70，21，15，105有如此神奇作用？70，21，15，105是从何而来？

这几个数的性质：70除以3余1，被5，7整除，所以70a除以3余a，也被5，7整除；21余以5余1，被3，7整除，所以21b除以5余b，也被3，7整除；15除以7余1，被3，5整除，所以15c除以7余c，被3，5整除。而105则是3，5，7的最小公倍数。

总之来说：70a＋21b＋15c是被3除余a，被5除余b，被7除余c的数，这个数如果大于公倍数105，便逐次减去直到得到23。

因此，一个数学难题的意义是在于得到它的通解以及进一步的推广。研究这个问题的主要的是一位宋朝数学家秦九韶，他才是对“物不知数”问题作出完整系统解答的人，载于1247年秦九韶的《数书九章》中，从而使这一问题变为了定理。再后来，《数书九章》由伟烈亚力在19世纪初译为英文，德国数学王子高斯在1801年对此类问题提出最早的完整系统解法。

图4：a）物不知数的通解

                         b）秦九韶和《数书九章》

                         c）高斯系统解决同余问题

（YouTube视频）

这个物不知其数的题目，推广成“中国剩余定理”是这么说的：

中国剩余定理成为数论中关于一元线性同余方程组的重要定理，说明了一元线性同余方程组有解的准则以及求解方法。

3. 古中国的“方程术”

上一节介绍的“韩信点兵”（物不知其数）问题，来自《孙子算经》。该书中还有很多有趣的数学问题，比如鸡兔同笼就是一个几乎人人皆知的著名数学题。“鸡兔同笼，头共10，足共28，鸡兔各几只？”，设鸡x，兔y：x+y=10, 2x+4y=28, 加减再消元，便可求得答案为4兔6鸡。这个问题非常简单，但却代表了代数中的一大类问题：n元一次方程组。具体对这道鸡兔同笼问题，就是解一个2元一次方程组。

二元（n=2）的意思是有x和y两个变量，“一次”是说只包含变量的1次项，说明方程是线性的。本题的方程组中有两个方程，才能解出两个变量。

中国古代数学著作中比较有名的，除了6世纪的《孙子算经》之外，还有早好几百年的《九章算术》。就成书的年代及篇幅而言，它们可以与古希腊数学相媲美。但中国数学书的特点是演绎和定理比较少，用现在的标准看起来，不像教科书，像是习题集和答案，再加上了有关解题方法的一些叙述。这是因为中国古代数学轻演绎重应用的原因。另外就是古希腊数学的重点是几何，古中国数学有更为浓郁的代数色彩，更像是7-8世纪的印度或阿拉伯的数学。

在《九章算术》中，第八章“方程”的第一道题目，就是解一个三元一次方程组（图1.7.5）。三个未知数，比鸡兔同笼问题多了一元，更为复杂一点。

图5：《九章算术》“方程术”中的代数题（YouTube视频）

我们可以用现有的代数方法解这道题：令 x, y, z 分別代表上等稻、中等稻和下等稻各1捆所能打出的稻米斗数，然后列出如图1.7.5右所示的三元一次联立方程组，经过分离变量和消元过程，便能得到图1.7.5右下角所示的x, y, z 数值。

图6：张苍和《九章算术》（YouTube视频）

张苍的年代稍后于阿基米德，大约是公元前200年左右的人士，阳武（今河南原阳）人。他不仅是西汉时期“以善算命世”的数学家兼天文学家，又是西汉的开国功臣，并且官至丞相十几年，他的政治声誉大于科技的。在数学方面，他是《九章算术》的作者和编辑者之一。

 
《九章算术》的“方程术” 一章：包括了联立一次方程组的解法和正负数的加减法，在世界数学史上是第一次出现。“方程”的地位相当于今天的线性方程组。“方程术”之算法上与今天加减消元法完全一样。这确实是中国古代数学一项了不起的成就，可以说超过中国剩余定理的意义，但是剩余定理融入了世界数学之中，方程术却只在中华文化中昙花一现，尽管也许解决了农业生产等等活动中的实用计算问题，但在闭关自守的环境下不被重视，无进一步的理论研究，最后被淹没而鲜为世人知。

《九章算术》中，对于开平方术、开立方术，叙述非常详尽，在当时也是很先进的方法。“方程术”与“开方术”相结合，后来发展了高次代数方程的“天元术” ，可以解出二项二次方程、二项三次方程，或更高次的方程，在数学的发展中也有重要地位。此是后话不表。

图7：用符号表示的“天元术”的3次方程

4. “尝拟雄心胜丈夫 ”

尝拟雄心胜丈夫，这句诗出自于中国清朝一位女数学家王贞仪。

你可能没听过这位女科学家，但她在世界上却有一定的知名度：金星上有一个以她命名的撞击坑，还有一颗小行星也以她命名。

图8：有关王贞仪的书和视频

王贞仪（1768～1797），字德卿，生于江宁府（今江苏南京），祖父宣化太守王者辅热爱读书，据说有藏书七十五橱，且精通历算，著述颇丰，父亲王锡琛科举不中，转而学医，精通医术。出身于如此家庭，自小聪明好学喜爱读书的王贞仪，从祖父学习天文，从祖母学诗词，父亲则教她医学、地理和数学。后来她又随同祖母和父亲去过北京、陕西、湖北、广东和安徽等地，游览名胜古迹，见闻颇多，也接触到不少社会实际。25岁时和安徽宣城的一个叫詹枚的青年结了婚，没有孩子，并且不幸于29岁时英年早逝。

王贞仪只活了短短的29年，但却留下不少著作。

数学著作有《西洋筹算增删》、《重订策算证讹》、《象数窥余》、《术算简存》、《筹算易知》、《勾股三角解》等。

文学作品《德风亭诗钞》和《德风亭集》。

天文学书籍：《岁差日至辩疑》、《盈缩高卑辩》、《经星辩》、《黄赤二道解》、《地圆论》、《地球比九重天论》、《岁轮定于地心论》、《日月五星随天左旋论一、二、三》、《月食解》

从她遗留下来的著作可以看出，她是一位从事天文和筹算研究的女数学家。

据说她曾积极宣传阐释哥白尼的日心说，这在当时十分难能可贵。她用自己的独立见解来诠释“天圆地方”，并对日月食的成因做出了通俗易懂的解释。她还对岁差的成因、测量和计算做出贡献。

她写过一本介绍西方“算筹”的书。算筹是一种棒状的计算工具，其作用类似算盘。应用“算筹”进行计算的方法叫作“筹算”。17世纪初叶，英国数学家纳皮尔发明了一种算筹计算法，明末介绍到我国，也称为“筹算”。清代著名数学家梅文鼎、戴震等人曾加以研究，还短暂地形成了一个安徽数学学派。王贞仪祖籍安徽，当年是这一学派的主要成员之一。她研究由西洋传入中国的这种筹算，并且写了三卷书向国人介绍。王贞仪思想开放，主张取中西算法之优点。对此，她在《勾股三角解》中有一段十分精彩的论述：“中西固有所异，而亦有所合。然其法理之密、心思之微，而未可以忽视。夫益知理求是，何择乎中西？唯各极其兼收之义。”

王贞仪酷爱天文，喜欢自己动手，她用屋顶横梁上悬挂的水晶灯当做太阳、小圆桌当做地球、圆形的镜子当作月亮。根据天文学原理，她一边移动这三个物体，一边不断地观察它们的相对位置和造成的现象，终于弄清了日月食的原理。她写了《月食解》一文，精确地阐释了月食发生的时间、食分深浅等知识，语言浅显直白，还有配图。王贞仪在她的另一部著作《地圆论》中，揭示了“相对空间位置的概念”，即宇宙没有上、下、正、反之分，以此而批驳流传了数千年的天圆地方之说。

她颇有文才，写诗填词懂绘画。“峰势长江矗，涛飞天外声。潜虬能护法，徵士独留名。”、“始信须眉等巾帼，谁言儿女不英雄？”是她的诗句。

××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××

本人的科普视频：YouTube：

天文航天：“談天說地”  https://www.youtube.com/playlist?list=PL6YHSDB0mjBLmFkh2_9b9fAlN7C4618gK

趣味数学：數學大觀園  https://www.youtube.com/playlist?list=PL6YHSDB0mjBJifi3hkHL25P3K9T-bmzeA

也发在微信公众号“天舸”上（微信号：gh_e01fc368fe31）:

              长按/扫一扫二维码，敬请关注我的微信公众号“天舸” !

××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××