万维读者网 -- 全球华人的精神家园

广告服务

联系我们

关于万维

首　页

新　闻

视　频

博　客

论　坛

分类广告

购　物




天蓉的博客
随笔、小说、诗词、科普。 “真和美，是科学不变的精髓；爱与死，是文学永恒的主题……”
		https://blog.creaders.net/u/5477/ > 复制 > 收藏本页

网络日志正文

		浅谈量子计算机-4	2023-12-19 13:30:25

浅谈量子计算机-4

4.2 多伊奇算法

上节介绍的Grover搜索算法，并不是第一个量子算法。第一个量子算法是由多伊奇发表的，多伊奇被誉为“量子计算之父”，是一位常人眼中行为奇特的科学家。

戴维·多伊奇教授是出生在以色列长在英国的犹太人，表面上，他是英国物理学家，牛津大学教授，量子计算先驱！不过他不教书，实际上是一个没有固定工作的自由学者。他靠着演讲、奖金和出书来赚钱为生，据说是位很少与人来往的牛津隐居者。

特别引起公众瞩目的，是多伊奇那两本可以当作科普来读却又与一般科普完全不一样的书：《真实世界的脉络》和《无穷的开始》。书中多伊奇有许多新奇深奥的科学哲学观点，在此我们不详谈，对他的书感兴趣的读者可阅读参考文献^【⁷^，⁸^】。

图4.7：多伊奇

总而言之，多伊奇这位两耳不闻窗外事的古怪科学家，在1985年突然声名大振，因为他发表了一篇里程碑式的论文，文中他展示了Deutsch算法，表明量子计算可以比经典更快。7年后（1992年）发表了对多伊奇算法的推广^【⁹^】。在多伊奇算法启发下的之后两年间，量子算法来到多产期。Simon、Shor和 Grover的算法都在这期间相继发表。

多伊奇算法没有什么应用，但作为第一个量子算法意义重大，它只适用于一种特殊的情况。因此作一个简要介绍。

考虑一个只有一个变量的函数，输入为0或1，输出也为0或1。这样的函数共有四个，分别记为f0、f1、f2和f3：函数f0，输入0和1，输出都是0，即f0(0) =0和f0(1) =0。函数f1，输出与输入相等，即f1(0) =0和f1(1) =1。函数f2，输出与输入相反，即f2(0) =1和f2(1) =0。函数f3，输入0和1，输出都是1，即f3(0) =1和f3(1) =1，见图4.7下图。

图4.8：多伊奇函数

我们将函数f0和f3称为常值函数，即对于两个输入，输出都是相同的值的函数。如果一个函数一半的输出是0，另一半的输出是1，那么就称这个函数为平衡函数。例如f1和f2就是平衡函数（图4.7上图）。

Deutsch提出的问题是：随机给定这四个函数中的一个，我们需要查询多少次，才能确定这个函数是常值函数还是平衡函数？就是说我们不关心给定函数是四个函数中的哪一个，只问它是常值函数还是平衡函数。

首先想想经典计算需要多少次？经典计算机一次只能有一个输入，也只能计算并输出一个函数值。但是，为了回答多伊奇问题，我们必须把0和1都代入函数，所以一定需要做两次经典操作。那么，如果使用量子计算机呢？量子计算机优于经典计算之处，是因为量子比特是叠加态，它可以同时储存1和0两个数。那么，就有可能操纵量子比特，同时对0和1进行计算，因此便有可能一次得出答案。实际上也可以做到，这正是多伊奇算法所展示的。

具体可用IBM模拟实例慢慢体会，在这儿首先直觉地理解一下，为什么量子计算可以一次做到？

从多伊奇4个函数的定义出发，考虑另一个相关的“二进制和”函数Fi = (fi(0) + fi(1))。我们发现：F0 = 0、F1 = 1、F2 = 1、F3 = 0。也就是说，二进制和函数Fi有这样的规律：对常值函数为0，对平衡函数，和值为1。

多伊奇的问题只是判定函数类型，是常值函数还是平衡函数？这是一种更为整体的性质，并不需要知道是fi中的哪一个。因此我们可以利用量子比特的叠加性，检查二进制和Fi = (fi(0) + fi(1)) 是0还是1？这样就能够1次作出判定，Fi是常值函数还是平衡函数。

图4.9：多伊奇算法

图4.10：实现多伊奇算法的量子电路

图4.9是多伊奇算法的解释，图4.10是实现多伊奇算法的具体量子电路。

实现多伊奇算法的电路，看起来简单，输入输出皆为2。包括一个Oracle函数门、X非门、H门、最后测量。只测量第一个Qubit，第二个不需要测量。

测量后便能1次判定fi的性质（如结果1，是平衡函数；结果0，是常值函数）。

图4.11：多伊奇-乔萨算法

多伊奇-乔萨算法想法是类似的，第一个比特推广到n个量子比特。测量前n 个量子位，如果测得|00 … 0态的话，说明f (x)是常数函数；如果测得的状态不是|00…0态时，说明f(x)是对称函数。

相对于经典算法的2ⁿ +1次计算，量子算法只需一次黑盒计算，实现了相对的指数加速。

4.3 秀尔算法-1（经典，数论部分）

最重要的量子算法是秀尔（Short）算法，假如有了可用的量子计算机，我们便可以用它破解RSA加密算法。RSA是保障银行安全常用的加密解密方法，它的基础是因数分解问题。加密过程中将两个互素数p和q相乘得到N = p*q。加密是作一次乘法就完成的简单操作，但是反过来的解码过程则非常困难。

RSA算法的解码过程需要将一个整数N 作“质因数分解” ，得到质数p和q使得N = p*q。对经典计算机，时间复杂度是指数级别。例如，要分解d个十进制数字的整数N，蛮力算法需要遍历所有素数p直到sqrt(N），检查是否p能整除N。分解 d=230的N需要10²⁵次运算。2021年最快的计算机每秒钟1200万亿次（1.2x10¹⁵ /s，也得运算2000年左右。

图4.12：秀尔算法和经典算法

然而，秀尔量子算法展示了：在量子计算机上，因数分解问题可以在N的多项式时间内被有效解决，即足够大的量子计算机可以破解RSA，见图4.12。IBM于2001年成功展示秀尔算法实例，使用7个量子比特的量子计算机，将15分解成3×5，之后又分解21=3x7。这两个数字都很小，但却表明了秀尔算法具体实现的可能性。

秀尔的整个算法，分为经典算法和量子算法两部分。经典部分完成可以在多项式时间内能用经典算法完成的计算，而将最困难的“傅里叶变换估算周期”，留给量子算法解决。如果用经典算法来“估算周期”，最好的情况也仍然是以指数增长。最有效的经典因式分解算法，称为通用数域筛选法，可实现d^1/3（N=10^d）运行时间指数。

概括秀尔量子算法：1，经典，因式分解化为周期查找问题；2，量子，傅里叶变换估算周期。首先介绍经典部分：将分解因子化为周期查找问题？这个“周期”是怎么回事呢？

20 世纪 70 年代，数学家们就知道，如果可以找到一个模指数函数的周期，那么因式分解大数N就会变得容易。模函数k(mod N)表示的是k除N ，即k/N，的余数。例如，如下恒等式a≡b(mod N) 的意思是说，整数a和b被N除的余数相同。

我们用如下几个实例来加深对模函数以及“模指数函数的周期”的理解。

例1：假设N=15和k=1，1(mod 15)=1，因为1/15余数是1。进一步，将k代入其它正整数：2(mod 15)=2、 3(mod 15)=3、……。当k=15的时候，15(mod 15)=0；而当k=16的时候，16(mod 15)=1，再回到了模函数值为1的情况。显而易见，除15余数为1的不止1和16，还有很多：1、16、31、46、61……。也就是说，模函数k(mod 15)，对整数k一直写下去的话，一定的周期后（15），数值会循环，写出的序列是一个周期为15的周期函数：1，2，3，……，0，1，2，3，……。

不过这不是我们感兴趣的周期函数，我们感兴趣的是另外一种，叫做“指数” 模周期函数。

例2：仍然以N=15为例，但这次不用正整数序列，而用某一个整数的“指数”序列来模N，比如，用2的“幂指数”形成的序列：1，2，4，8，16，32，64，128，256 …

也就是序列：2⁰，2¹，2²，2³，2⁴，2⁵，2⁶，2⁷，2⁸ … （1）

用2的“幂指数” 序列（1）模15之后，得到另一个序列：

1，2，4，8，1，2，4，8，1 … （2）

可以看出，这个序列 (2) 的周期是4，我们将其称为 “指数a=2” 的模周期，用r表示。在这个例子中，N=15，a=2时，模周期r=4。除了2的“幂指数“序列外，也可以用其它整数a的幂指数序列，如以下例3所示。

例3：例如给定a=7，然后，给定幂指数序列：1，7，7²，7³，7⁴，7⁵ …，用这个序列模 15之后，得到的序列是：

1，7，4，13，1，7……

这个序列的周期r正好也为4。

例4：对2的“幂指数”序列模 21后得到：1，2，4，8，16，11，1，2，4 …，周期r是6。

数论学家们发现这种“指数” 模周期r，对整数N的素因子分解大有用处！一旦得到了周期r，并且r是个偶数的话，N就可以被分解成两个素数的乘积，为什么呢？

周期r被定义为满足a^r≡ 1(mod N)的最小正整数，另外我们又有1≡ 1(mod N)。将上面两个式子相减可得：

(a^r-1)≡ 0(mod N)。（3）

此外，如果r是偶数，(a^r-1) 可以因式分解为两个因子的乘积：

(a^r-1) = (a^r/2+1) (a^r/2-1)。（4）

图4.13：秀尔算法中经典部分

图4.13总结了秀尔算法中经典部分的算法。根据公式(3)，(a^r-1) 是N的倍数，然而，因为周期r是满足条件(3)的最小正整数，再与 (4)结合起来看，说明a^r/2-1和 a^r/2+1不是N的倍数，但它们的乘积(a^r-1)却是N的倍数。

假设N可以分解为两个素数因子p1、p2的乘积，即N=p1p2。上一段分析而得到的结论只在下面条件下才能成立：，p1 、p2分别是a^r/2-1、 a^r/2+1的素因子。因此，我们可以通过计算最大公约数： gcd(N, a^r/2-1) 及gcd(N, a^r/2+1)，来找到p1和p2 ，也就是将N分解。

可以用上面的例4进行具体计算来说明这个过程。例4中，N=21，a=2，r=6，周期r是满足a^r≡ 1(mod N)的最小正整数，即2⁶≡ 1(mod 21)。因为r=6=3x2，是偶数。

可写成8²≡ 1(mod 21)，此外我们又有：1²≡ 1(mod 21)；两式相减得：(8²-1²)≡ 0 (mod 21)

或者：(8+1) x(8-1) ≡ 0 (mod 21)。然后我们计算最大公约数：

GCD(21, 9)=3，GCD(21, 7)=7，所以，N（=21）可因式分解为：21=3x7。

这个例子可以推广到一般情况，因此，只要找到了指数模周期r，便能将N分解成质因数p1、p2的乘积。然而如何寻找指数模周期r呢？这就要借助于量子算法来加速计算。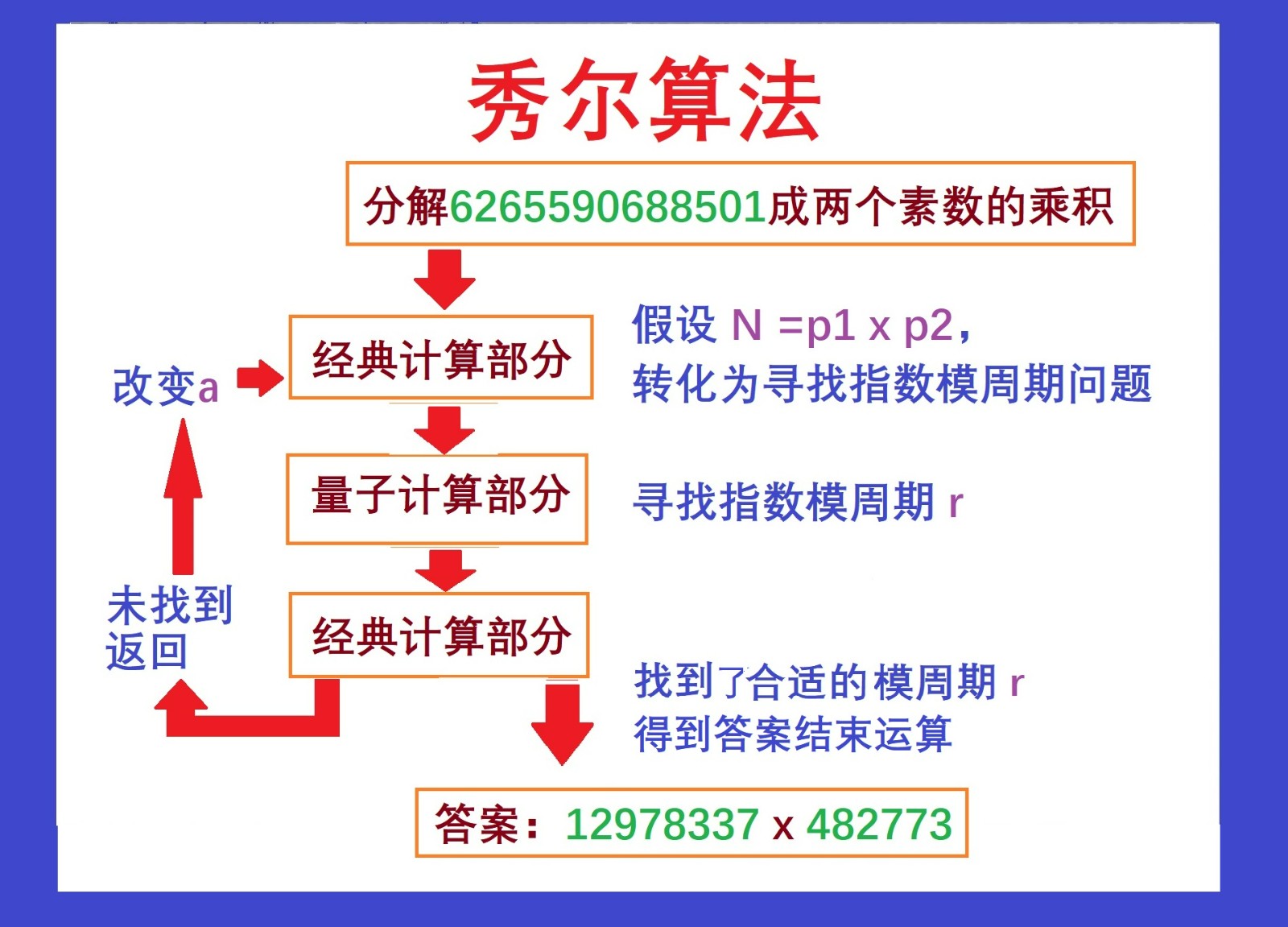

图4.14：秀尔算法总体流程图

4.4 秀尔算法-2（量子部分）

（待续）

参考文献：

【1】Keynote talk, 1st conference on Physics and Computation, MIT, 1981。(International Journal of Theoretical Physics, 21: 467–488, 1982)

【2】Thomas H. Cormen; Charles E. Leiserson; Ronald L. Rivest; Clifford Stein; 殷建平等译. 第1章算法在计算机中的作用. 算法导论原书第3版. 北京: 机械工业出版社. 2013年1月

【3】张天蓉. 世纪幽灵-走近量子纠缠（第二版）[M].合肥：中国科技大学出版社，2020年5月。

【4】Bloch Sphere（wikipedia），https://en.wikipedia.org/wiki/Bloch_sphere

【5】IBM Quantum (2022). estimator primitive (Version x.y.z) [computer software]. https://quantum-computing.ibm.com/

【6】Grover L.K.: A fast quantum mechanical algorithm for database search, Proceedings, 28th Annual ACM Symposium on the Theory of Computing, (May 1996) p. 212

【7】无穷的开始: 世界进步的本源，作者:戴维·多伊奇 (David Deutsch), 王艳红, 张

出版社：人民邮电出版社，出版日期：2014-11-01

【8】真实世界的脉络，作者: [英] 戴维·多伊奇，出版社: 广西师范大学出版社，译者: 梁焰 / 黄雄，出版年: 2002-8

【9】David Deutsch & Richard Jozsa (1992). "Rapid solutions of problems by quantum computation". Proceedings of the Royal Society of London A. 439 (1907): 553–558.

【10】Shor’s algorithm from IBM：

https://quantum-computing.ibm.com/composer/docs/iqx/guide/shors-algorithm