正如物理学家、曼哈顿计划领导者奥本海默所说:“我们不仅是科学家,我们也是人。”,有人的地方就有江湖,科学界也难免。人们经常说“科学无国界,科学家有祖国“,即使不谈这些政治纠葛,科学家中还是有不同学术圈子的,每个人都有自己坚持的学术观点和主张,学术争论无时不在。一般来说,自由争论有利于学术进步,但争论也可能造成误会产生偏见,从而让某些科学家受害并影响科学的正常发展。今天将讲述的,是AI历史中的一段江湖故事…… 1.罗森布拉特的感知器 1958年7月,美国海军研究办公室公布了一项非凡的发明,宣称展示了“第一台能够拥有人类思想的机器”,见图1。 演示者将一系列打孔卡经过一个电子设备,输入到一台重5吨,大小相当于一个房间的计算机(IBM704)中,经过50次试验后,计算机学会了区分左侧标记的卡片和右侧标记的卡片。换句话说,就是这个机器可以学会“分类”,如同孩子在父母的教导下学会分辨猫和狗一样。分类是人工智能研究的一个重要功能。 
图1:罗森布拉特和感知器Mark-1 美国海军演示的是“感知器”(或称感知机,Perceptron)。据其创造者,弗兰克·罗森布拉特博士介绍,这是一种模拟生物学中“神经网络”原理构建的电子设备,具有学习能力。罗森布拉特在1962 年出版的《神经动力学原理:感知器和大脑机制理论》[1]一书中详细分析并扩展了这种方法。当年,罗森布拉特因感知器而获得了国际认可。《纽约时报》将其称为一场革命,标题为“新海军设备通过实践来学习”,《纽约客》同样也对这项技术进步表示了赞赏。 当时的罗森布拉特是纽约布法罗康奈尔航空实验室的研究心理学家和项目工程师,展示感知机后的第二年,他成为康奈尔大学生物科学系神经生物学和行为学副教授。 罗森布拉特的感知机计划受到了McCulloch和Pitts的形式神经网络的启发,是专为图像识别而设计的一个简单的单层神经网络,并且添加了额外的机器学习机制。图2是感知机的逻辑示意图。感知机获得了美国海军的大量资助,最初是基于两年的软件研究而实现。之后,罗森布拉特构建并展示了感知器的唯一硬件版本:Mark-1,它由联结到神经元的400个光电细胞(20×20的感光单元矩阵)组成,可以将输入的光学信号(例如英文字符)转化为电信号,再通过物理电缆将其与字母分类的神经元层相连。Mark-1突触的权重函数用电位计编码,由电动马达实现学习过程中权重的改变。 可想而知,在当时的技术条件下,这台机器的具体实现还是非常困难的,这也是为什么引起轰动和广泛关注的原因。 图2:感知器设计概念图(1958年) 罗森布拉特对他的感知器寄予厚望,对人工智能神经网络的研究持十分乐观的态度,他乐观地认为突破即将到来。原来十分低调的科学家突然走红,他出席各种演讲、晚会,这点当然会引起当年人工智能大伽们的注意。 罗森布拉特的工作引起了MIT闵斯基教授的关注。闵斯基在感知器问世的两年之前,即1956年,与麦卡锡等一起,发起召开了达特茅斯研讨会,确定了人工智能的名字,讨论了发展方向等等问题。基于他对神经网络的研究,使得他对罗森布拉特的主张深感怀疑。科学中的质疑是正常现象,因此,他们经常在学术会议上公开辩论感知机的可行性。在一次会议上,两人大吵一顿,矛盾彻底公开化。想必那几次争论是非常激烈的,因为据他们的同事和学生在后来的回忆中,有“在一旁看得目瞪口呆”、“被他们的争论吓了一跳”之类的话语。闵斯基直接对感知机存在的价值和前途发起进攻,指出它的实际价值非常有限,没有什么发展前途,绝不可能作为解决人工智能的问题的主要研究方法。 “罗森布拉特认为他可以使计算机阅读并理解语言,而马文·闵斯基指出这不可能,因为感知机的功能太简单了”一位当年的研究生回忆说。 后来,1969年,闵斯基和MIT的另一位数学教授西摩·佩珀特(Seymour Papert)出了一本名为《感知机》(Perceptrons)的学术著作[2],从理论上证明感知机的缺陷,书中还有对罗森布拉特个人的攻击言语:“罗森布拉特写的论文,大部分内容……毫无科学价值”。 在《感知机》这本书对罗森布拉特工作的强烈抨击下,本质上终结了感知机的命运。次年,闵斯基获得图灵奖,得到了计算机领域的最高荣誉。 闵斯基是当时业界的权威人物,这种对感知机直截了当的负面评价,对本性孤傲的罗森布拉特来说是致命的。一年多后,罗森布拉特在独自划船庆祝自己43岁生日那天溺水身亡,把他的名字,他的感知机,他的遗憾和梦想,都永远留在了人工智能的科学史上。 《感知机》一书不仅打击了罗森布拉特,造成感知机的暂时失败,还几乎扼杀了当时神经网络方面的研究,也影响和带来了人工智能长达10年的第一次低谷期。 2.符号主义和联结主义 其实,罗森布拉特[3]和闵斯基的出身和经历,有许多相同之处,他们年龄相仿,都是出生于纽约的犹太家庭,他们甚至曾经同时就读于同一所中学,是纽约布朗克斯科学高中的校友。不错!就是那所出了8名诺贝尔科学奖和一位诺贝尔经济奖得主,还有难以数计的各方名人的著名高中。如此名校的学兄学弟,却结怨于学海江湖!不由得使人脑海中划过那句名言:“相煎何太急?” 不过,罗森布拉特去世后,闵斯基在《感知机》一书再版时,删除了原版中对罗森布拉特的个人攻击的句子,并手写了“纪念罗森布拉特”(In memory of Frank Rosenblatt)一语,多少表示了对这位早逝校友同行的哀悼。 此外,两人的争论也代表了当年人工智能中符号主义与联结主义两种学术观点之争[4]。 马文·闵斯基(Marvin Minsky,1927—2016)生于纽约市,他是深度学习的先行者。在哈佛大学读本科期间,他曾开发了早期的电子学习网络。在普林斯顿大学念研究生时,他建造了第一台神经网络学习机SNARC。他的博士论文以《神经-模拟强化系统的理论及其在大脑模型问题上的应用》为题,这实际上就是一篇关于神经网络的论文。所以,闵斯基研究生阶段的工作,奠定了人工神经网络的研究基础,应该属于联结主义的范畴。 1956年,他与约翰·麦卡锡、克劳德·香农等,一同发起了1956年的达特茅斯学院会议,创造了“人工智能”一词,是AI的开山鼻祖之一。达特茅斯学院会议也是符号主义的胜利,闵斯基和麦卡锡都被认为是AI符号主义的典型代表人物,当年他们的意图,是反对早期控制论的联结主义。认为人工智能的目的是通过程序在计算机中实现规则,用逻辑推理来对抗AI中的联结主义。从20世纪60年代中期到90年代初,符号主义方法盛行。 可见,闵斯基后来转向了符号派,他也尽力淡化他与联结主义间的关系,也许这是他强烈抨击感知机的原因之一。 闵斯基自1958年起在麻省理工学院任教,担任电子工程与计算机科学的教授,直到他过世为止。 在麻省理工学院,他与约翰·麦卡锡共同创立了人工智能研究室(MIT计算机科学与人工智能实验室的前身)。他有数项发明,如1957年发表的共聚焦显微镜,1963年发表的头戴式显示器等。 2016年1月24日,闵斯基因脑内出血病逝,享寿88岁。 闵斯基的对手弗兰克·罗森布拉特(Frank Rosenblatt,1928-1971)比他小一岁,是一位心理学家。 罗森布拉特出生于纽约长岛的一个犹太家庭,1946年从布朗克斯科学高中毕业后,他进入康奈尔大学,并于1950年获得学士学位,1950年获得博士学位。随后,他前往纽约州布法罗的康奈尔航空实验室,先后担任研究心理学家、高级心理学家和认知系统部门负责人。这也是他进行感知器早期工作的地方。 罗森布拉特1966年加入康奈尔大学新成立的生物科学系神经生物学和行为科,担任副教授。他对通过注射脑提取物将学习行为从经过训练的老鼠转移到小老鼠身上产生了浓厚的兴趣,他在后来的几年中就这一主题发表了大量文章。 罗森布拉特也对天文学感兴趣,他花了3000美元买了一台望远镜,但太大了以至于没有地方放。因此,他在纽约布鲁克顿代尔附近买了一栋大房子,并邀请他的几名研究生住在那里。白天,团队在托伯莫里工作。晚上,他们在罗森布拉特的院子里作土木工作,建了一座天文台。 罗森布拉特兴趣广泛多才多艺,白天在实验室里解剖蝙蝠,研究动物大脑的学习机理,夜晚在自家后山搭建的简易天文台上仰望天空,试图探索外星人奥秘。罗森布拉特的性格方面,害羞内向,并不张扬。 感知器始终是罗森布拉特的热情所在。他最终没有熬过人工智能的冬天,于1971年43岁生日那天,自驾驶帆船溺水身亡。2004年,IEEE计算智能学会设立了罗森布拉特奖(IEEE Frank Rosenblatt Award),奖励在生物及语音启发计算领域做出卓越贡献的人,以纪念这位杰出的科学家。 图3:当年的感知机相关文章和书 1956年的达特茅斯会议,启动了第一波人工智能浪潮,这一浪潮跨越至70年代初,代表符号主义的建模推理方法是其核心特征。这方面研究的主流由MIT的闵斯基、卡内基梅隆大学的西蒙和纽厄尔,以及斯坦福大学的麦卡锡组成。在当时,这个符号主义圈子里的高手们,基本建立了对人工智能问题的垄断,并获得了大部分资金和大型计算机系统的访问权。 符号主义者的主要特征是他们不太重视机器智能与世界的联系,只在计算机内开辟独立的推理空间,将人工智能视为机器思维的科学,目标是赋予机器以逻辑和抽象的能力。 反之,罗森布拉特是心理学家,对人类生理学和心理行为等更感兴趣,因而趋向于联结主义。自然地,他热衷于对用神经网络的概念来模拟人脑神经传递机制,也由此而研究发明了感知机。 感知机在媒体上取得的成功,也激发起联结主义研究人员的热情。但闵斯基和帕佩特在1969年的书中宣称他们证明了神经网络无效的说法,又给这些科学家们浇了一盆冷水,使联结主义的热度骤减。尽管这本书的影响可能超出了闵斯基等的意图,但其后果是确定的:神经网络被放弃,其资金被大量削减。实际上,不仅联结主义衰退,针对符号主义的批评也越来越多,符号主义和联结主义项目都被冻结了,联邦对人工智能研究的资助枯竭。人工智能被当成仅仅是人工游戏,进入了它发展旅程中的第一个冬天。 3.感知器和神经网络 我们回到罗森布拉特的感知机[5]。它实际上是现代神经网络的雏形,有没有科学价值,已有如今AI的迅猛发展为证。当然,作为第一代的人工智能机器,感知器有这样那样的缺陷是难免的,而且当时的罗森布拉特,还没来得及把感知机的学习算法推广到多层神经网络。神经网络从简单到复杂多种多样,见图4。感知器只是一个最简单只有一层的神经网络(图4左),而现代神经网络却有数百万个(隐藏)层,图4右。 图4:感知机和复杂神经网络 不过,闵斯基认为感知器的缺陷是致命的,因为它无法模拟“非线性可分”函数,他举了一个逻辑门的例子:异或门,即感知器不能区分异或门。以下对此作简单介绍。 感知器神经元的简单模型如图4左图所示:多个输入和一个输出。输出功能是求得输入向量与权向量的内积后,经一个激活函数得到一个标量结果。 神经网络为什么能分类呢?原因之一是归于激活函数的功劳。例如,最简单的激活函数是个阶梯函数,输出0或1,也就是说,这个函数实现了分类:将结果分成了两类。 至于何时输出0,何时输出1?就要根据输入的值来进行决策了。例如,可以问3个问题来判定是猫还是狗?耳朵朝上还是朝下?嘴巴是否凸出来?胡须长或短?最简单的决策方法就是:3个问题都输入yes的话,输出=猫,否则是“狗”。但激活函数可以从阶梯函数改变为平滑的函数,如图4左图中右下角的红线所示,这种函数便于在最优化时进行微分计算,而输出便被相应地理解为决策判断为是猫还是狗的概率了。 神经网络又为何能具有学习功能呢?那是因为每个输入端都有一个权重值,这些参数是神经网络的核心。在训练过程中,网络调整这些权重,以使其在特定任务上的误差最小化。这个权重更新的过程也就是所谓的“机器学习”的过程。最小化可以使用各种优化算法,例如,感知器中用的是“梯度下降法”。 如图4左图上方的公式所示,为输出而计算的求和函数是n维空间中的一个超平面。因此,感知器这种神经网络“分类”的本质就是这个超平面将空间分成了两部分。如果对两个输入端的神经网络而言,就是用一条直线将平面分成了2个部分,如图5b所示的线性可分情况。
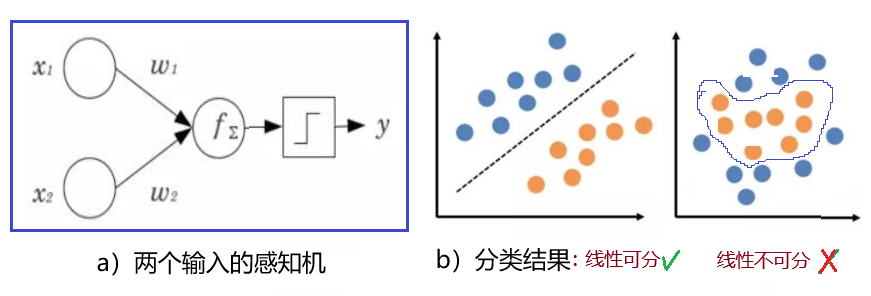
图5:感知机分类,线性可分和不可分 然而,如果输入的样本是线性不可分的(图5b右边),感知机则无法模拟这种情况。这就是闵斯基指出的感知机的缺点。 图6显示的是几种基本逻辑门的情况,单层感知机可被用来区分其中的3种,逻辑与(AND)、逻辑与非(NAND)和逻辑或(OR),但是,无法模拟逻辑异或函数,因为它属于线性不可分。 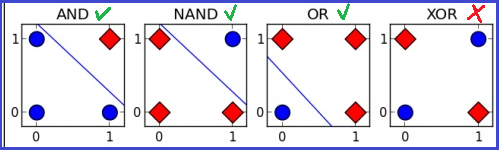
图6:逻辑门,前3种是线性可分的,XOR非线性可分 要解决非线性可分问题,可考虑使用多层功能神经网络。输出层与输入层之间的一层神经元,被称为隐层,隐层和输出层神经元都是拥有激活函数的功能神经元。图7左图中,感知器的神经元,没有隐含层,决策计算只生成一条直线,无法区别异或问题。但如果增加一个带非线性激活函数的隐含层就可以了。隐层输出的激活函数的非线性也有助于解决非线性可分问题。多一个隐层相当于增加了一个空间维度,如图6右图所示,构成了一个单隐层的神经网络,决策计算就能生成两条直线,可以区别异或问题了。 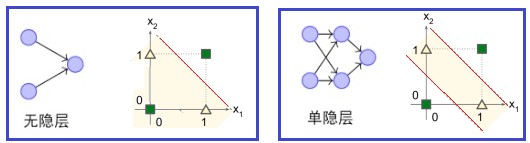
图7:加一个隐层解决感知机的异或问题 对多隐层的神经网络,还有一个“万能近似定理”,意味着使用S型函数作为激励函数的多层神经网络,可以用来近似任意的复杂函数,并且可以达到任意近似精准度。 总而言之,从20世纪80年代和90年代开始,联结主义重新出现,神经网络研究回归主流。许多人认为罗森布拉特的理论已被证明是正确的。朴素的感知器有其缺陷,但它的基本原理引发了现代人工智能革命。深度学习和神经网络正在改变我们的社会,了解一下感知器,以及神经网络这段兴衰史,有助于我们更好地认清AI,以及AI发展的未来。 参考文献: [1]Rosenblatt, Frank (1962). “A Description of the Tobermory Perceptron.” Cognitive Research Program. Report No. 4. Collected Technical Papers, Vol. 2. Edited by Frank Rosenblatt. Ithaca, NY: Cornell University. [2]Minsky, M. L. and Papert, S. A. 1969. Perceptrons. Cambridge, MA: MIT Press. [3]https://en.wikipedia.org/wiki/Frank_Rosenblatt [4]科普中国:人工智能的三大学派 https://www.kepuchina.cn/zt/salon/tsrgzn/201901/t20190123_924578.shtml [5]维基百科=感知器 https://zh.wikipedia.org/wiki/%E6%84%9F%E7%9F%A5%E5%99%A8
|
