杰佛瑞·埃佛勒斯·辛顿（Geoffrey Everest Hinton，1947－）【1】，被誉为“AI教父”，他一生的理想是要明白“人的大脑是如何工作的”？机器是否能模仿大脑的运作机制？为此他花了半个世纪的时间开发神经网络，他在1986年和2022年，分别发表了两篇与神经网络算法相关的重要论文，一前一后相隔三十多年，一反一正都是讨论机器如何学习的问题。哪一种算法更接近人脑的运作模式呢？辛顿对此有与众不同的观点，此文将为你解读这两篇文章的核心思想，然后，你对上述问题便能得出你自己的答案了。

图1：辛顿的两篇论文

反向传播算法

1986年，辛顿与David Rumelhart和Ronald Williams共同发表了一篇题为“通过反向传播误差来学习”（Learning representations by back-propagating errors）的论文【2】。

三位科学家并不是第一个提出这种“反向传播”方法的人。但他们将反向传播算法应用于多层神经网络并且证明了这种方法对机器学习行之有效。他们的论文也证明了，神经网络中的多个隐藏层可以学习任何函数，从而解决了闵斯基等书中提出的单层感知机存在的问题。

“反向传播”是“误差反向传播”的简称，是人工神经网络的一种自我学习算法。说到学习，我们自然地联想到人类大脑的学习过程，例如孩子学习识别“猫和狗“那样，是从反复的经验和错误中学习。机器学习也是这样，我们在计算机中，首先构造一个由输入层、输出层，以及多个隐藏层组成的多层神经网络，这就像给计算机建造了一个”人工大脑“。然后，我们需要训练这个大脑，让它学习使其具有”智能“。学习和训练有各种方法，“深度学习”是其中一种，这个方法由“梯度下降”和“反向传播”反复迭代而完成。下面以“识别手写数字“的例子来简要说明这个过程，图2。

手写数字的每个样本，比如图2中所示的“2”，被扫描后用28*28=784个实数替代，送到神经网络的输入节点上。这个神经网络，除了784个输入节点外，还有10个输出点，表示从0到9的数字。输入和输出中间有两个隐藏层（每层16个节点），第一个隐藏层分辨数字图像中的一些小片段，第2层则分辨“圈”“线”一类的笔画结构，然后，根据样本图像所具有的结构，输出层得出判断：是0到9中的哪一个。

类似于人体的神经系统，不同神经元之间有不同的关联，人工网络中节点与节点之间的关联用一系列权重参数wi来表示。也可以说，权重参数wi代表了节点激活下层节点的概率。参数wi的数目很多，即使是图2中这个简单4层网络的例子，所有的wi参数加起来也有1万3千多个，训练的目的，就是要调节好这些权重参数。此外，每个层之间还有一个激活函数，一般可以是不连续的阶跃函数，或者常用的平滑可微的sigmoid函数（图2神经网络上方所画曲线）。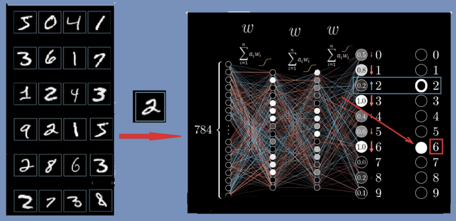

图2：识别数字的例子

一开始的w参数，是随机选取的，因此，神经网络的判断会出错。例如在图2中，输入的是2，它却认成了“6”，那怎么办呢？就像小孩犯了错误一样，我们需要反复教他。机器则需要使用大量的数据来训练它，这就开始了“机器学习”的过程。

如何让机器学习呢？首先要知道错误的来源，那就是来源于这13000个权重参数（可能还包括其它如偏差、激活函数的参数等），因为，最后结果就是用它们代入一个求和公式再乘以激活函数逐步进行运算而得到的。所以，为了调整这些参数，我们根据神经网络从输入计算输出的方法，定义一个误差函数C(wi)（或称代价函数、目标函数），如图3b下方所示C(wi) 的表达式。这样，训练的过程就是反复调整wi，使误差C(wi)达到我们能接受的最小值。

这些参数wi对误差函数C(wi)的影响，或称敏感度，是不一样的，所以每一次对每个参数调整的幅度也不一样。敏感度，用数学术语表达，就是梯度。在2维情况下，梯度可以形象地被理解为通常意义下山坡的坡度。坡度有方向，一般指的是一个向上的矢量，向下就叫负梯度，见图3。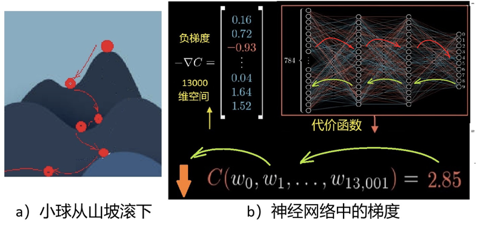

图3：梯度下降和反向传播

深度学习中的梯度，原则上与山坡坡度类似，不同的是它是在非常大（上万上亿）的维度空间中的“矢量”。二维情况的梯度可以很容易地画图（图3a）理解，但图3b中13000维空间的矢量就无法直观想象了，不过数学上仍然可以定义“梯度”的概念。

要使误差函数C(wi)达到最小值，类似于我们想从山顶到达谷底。如何找到最优路径，在最短的时间内到达呢？直觉告诉我们应该朝最陡峭的方向下降，就是说任何时候都选择最陡的（最大坡度）的反方向往下走。这就是机器学习中说的梯度下降算法。不过事实上，梯度下降是一种标准的优化算法，并不是仅仅用在机器学习中。

13000维空间中的梯度计算起来很复杂，而所谓“反向传播”就是用来计算这个复杂的“梯度”的。在数学上，就是利用微积分中的链式法则，来计算偏导数继而计算梯度。

输出结果（误差）被视为是正向计算（如图3b中的红箭头线指向）。要计算敏感度，即每个参数对误差的贡献，则可以逐层反向计算回去，如图3b的绿箭头线所指。这个过程就是误差反向传播，有点像在某项工作中出现了事故后，一层一层反回去秋后算账追究责任的过程。

借助于反向传播，所有的参数得以调整，然后，又根据调整后的参数正向计算出结果，即误差。如此过程反复循环直到误差函数C(wi)接近0，或降到一个我们满意的数值为止。

当然不能只用一个样本，比如例子中原来那个“2”，如果那样训练出来的机器只能识别那一个“2”。我们需要使用成千上万的不同数字的样本来训练这个神经网络，最后才能让它正常工作。 

以上学习方法中，反复的“正向”和“反向”，计算来回进行在输入端输出端之间，故也称其为“端到端”的方法，“Back Propagating”也简称为BP算法。

反向传播的问题‍‍

反向传播算法（BP）是人工智能历史上一个重要的里程碑，这一算法的提出使得多层神经网络的学习问题得到了有效解决，为非线性分类和学习提供了可能。基于这种算法，多层人工神经网络的机器学习逐渐形成了固定的模式，人工神经网络的研究才重新焕发生机，AI的发展也进入了兴盛期。

使用BP的深度学习，逐渐应用扩展于自然语言处理、语音识别、图像识别等领域，解决了许多实际问题，使得人工智能在各个领域取得了显著进展。反向传播法是深度学习当年取得成功的关键，至今仍然是这个领域的重要基础之一，它不断推动着人工智能的进步。

数学上，BP算法中误差的反向传播过程，采用的是已经非常成熟的链式法测，其推导过程严谨且科学，使神经网络具有很强的自主学习能力，拥有较强的非线性映射能力，这是它的根本以及其优势所在。此外，BP算法也具有较强的泛化和通用能力，可以利用从原来知识中学到的知识，解决碰到的新问题。

然而，随着研究的深入，也逐渐显现出BP算法的某些缺陷，这使得神经网络的发展面临一定的挑战。反向传播算法存在几个问题：一是计算出来的梯度是否真的是学习的正确方向。这在直观上有些可疑。此外，从数学角度看，BP算法是一种速度较快的梯度下降算法，但由于BP神经网络中的参数非常多，当网络包含数百万或数十亿个参数时，也导致有时候收敛速度过慢。并且，梯度下降法容易陷入局部最小值，这时从表面上看，误差符合要求，但所得到的解并不一定是问题的真正解，所以BP算法是不完备的。

因为BP算法依赖于前向传递中计算的可微性，如果某个环节存在不可微的情况，则反向传播便无法进行。例如，如果我们在网络中插入一个黑匣子，除非我们知道黑匣子的可微模型，否则将不可能执行反向传播。

作为反向传播这一深度学习核心技术的提出者之一，辛顿很早就意识到反向传播并不是自然界生物大脑中存在的机制。虽然反向传播非常有用，但它与我们对大脑的了解有很大不同。

近几年，辛顿在不同场合的演讲中都提到这个问题，他的要点是将这种方法与人脑的机制比较：

“作为皮层如何学习的模型，反向传播仍然令人难以置信，尽管人们付出了相当大的努力来发明可以由真实神经元实现的方法”，“没有令人信服的证据表明皮质明确传播错误导数或存储神经活动以用于随后的反向传播。”

反向传播中，学习和推理过程是分离的。训练时，算法必须经常停止推理，以执行反向传播来调整权重参数，这有别于人脑。我们的大脑源源不断地接收到信息流，并且实时不断地进行推理，似乎不像有停下来进行反向传播的过程。

尽管目前BP算法正在业内用得热火朝天，但有远见卓识的大师总是未雨绸缪，考虑的是AI的未来，因此，辛顿根据他的最新研究，在2022年发表了一篇论文【3】，主要有两个主题。

一是介绍了一种新的人工神经网络学习算法“forward-forward algorithm”，简称为FF算法。二是提出了一种新的“凡人计算”模型。下面两节分别作简要介绍。

前向-前向算法

前向-前向算法是一种贪婪的多层学习程序，不同于BP算法的“端到端”（图4左），它是将学习过程一层一层地完成（图4右），在每一个单层内反复计算直接更新参数。也可以理解为，FF是用两个前向传播，代替BP的前向+后向传播，两个前向计算定格在不同的数据和相反的目标上，以完全相同的方式彼此操作。BP算法中的“代价函数”，在FF算法中，被代之以另一个术语：”好感度“（goodness）。换言之，“正计算”对真实数据进行操作，并调整权重以增加每个隐藏层的好感度，“反计算”则调整"负数据"权重，以减少每个隐藏层的好感度。此外，如果前向和反向通道可以在时间上分开，反向传递可离线进行，这将允许数据通过网络正常运行，而不需要暂停传播。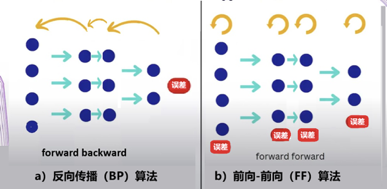 

图4：BP算法和FF算法

与反向传播不同，FF 算法在包含黑盒模块时也有效。由于该算法不需要可微函数，因此它可以在不知道模型中每一层的内部工作原理的情况下，仍然可能调整其模型的可训练参数。

辛顿在由四个全连接层组成的神经网络上测试了FF算法，每个层包含2,000个神经元。从他的实验结果，辛顿认为，FF算法仍处于早期实验阶段，比较BP算法，它在速度上要慢一些，但也基本上可以相媲美，其优势在于可以在前向计算的精确细节未知时使用它，例如使用黑盒模型。辛顿也说，在他用FF算法研究的几个玩具问题上，通用性不是很好，所以FF也许不会完全取代反向传播的应用，但FF有两个意义，首先，它是更为接近大脑皮层的学习模型，其二，它在功率成为问题的应用中有意义。

辛顿的FF算法是他从人脑运作中汲取灵感而提出的。虽然人工神经网络企图仿照人类大脑的功能，但许多方面有很大的差别。例如在耗能方面，人脑约有860亿个神经元，形成复杂的神经环路和网络，但其能耗只有20瓦。而大小类似的人工神经网络的能耗约为8百万瓦【4】，是大脑的40万倍。这个差别的根本原因是由于现代计算机的构型所决定的。

辛顿在提出FF算法的论文中，也挑战了既定的计算范式，提出了一个新的方向：凡人计算。

凡人计算

听起来这是一个奇怪的名字，是从英文“Mortal computation”翻译而来，这是什么意思呢？

在计算领域，传统上强调硬件和软件的分离。这种分离有许多优越性，它允许在不深入研究硬件的情况下研究程序，它还允许在数百万台计算机上使用同一个软件。但是，这种分离是有代价的，也完全不同于人脑的工作方式。

人类大脑显然没有什么硬件软件之分，人的智慧和知识，与他的“大脑”实体密切相连不可分，一个人死去了，他的智力也就消亡了，不可能“copy”给另一个人使用。也就是说，人不能“永生”，人类的智力也不能“永生”，而人工智能中的“计算程序”，却是“永生”的，不会因为某台机器的毁坏而消亡。可以比喻说，目前的“计算”，是个不会死亡的“超人”，而辛顿提出“凡人计算”概念的意思，就是要挑战此类超人，让计算，也就是程序，模拟真正的“凡人”。

为什么要计算成为不能“永生”的凡人呢？因为“永生”需要付出极大的代价，上一节所举的机器能耗与人脑能耗的巨大差异（8百万瓦：20瓦）就是其中之一。

从硬件角度看，现有AI系统是基于通用的CPU和GPU，它们都是根据冯诺依曼结构的集中式内存设计的，见图5。存储器与其它部分有一定距离。因此，计算过程中数据的搬运造成延迟、耗费能量；而人脑中的基本计算单元都是存算一体的，相当于数据和计算都是分布式的，每个基本单元，既完成计算也存储信息。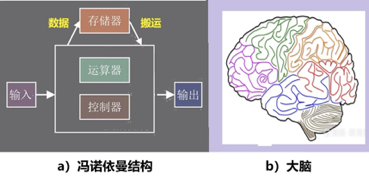

图5：计算机结构有别于大脑结构

冯诺依曼的通用数字计算机，被设计为忠实地遵循指令，即编写一个程序，以极其详细的方式准确地指定机器要做些什么。辛顿在其新论文中，提出改变这种“计算程序永生”范式的设想。

辛顿写道：“如果……我们愿意放弃永生，那么执行计算所需的能量和制造执行计算的硬件的成本应该可以大大节省。我们可以允许旨在执行相同任务的不同硬件实例的连接性和非线性发生较大且未知的变化，并依靠学习过程来发现有效利用每个特定实例的未知属性的参数值的硬件。”

辛顿的想法意味着软件要逐渐地构建在每个硬件上，并且只对那个硬件有用！即软件变成了与硬件一起消亡的“凡人”！辛顿认为，尽管这种“凡人计算”存在缺点，但具有明显的优势。特别是，如果你想让你的万亿参数的神经网络能耗降到几瓦特的话，“凡人计算”恐怕是唯一的选择。

辛顿也谈到寻找可以在这样的精确硬件中高效运行的学习程序的问题：或许FF算法就是一个有前途的候选者，尽管它对大型神经网络的扩展能力还有待观察。

总之，辛顿这一突破性的想法有可能彻底改变神经网络的功能，影响人机交互过程，甚至刷新我们对意识的理解。

参考文献：

【1】Home Page of Geoffrey Hinton，https://www.cs.toronto.edu/~hinton/

【2】David E. Rumelhart, Geoffrey E. Hinton und Ronald J. Williams. Learning representations by back-propagating errors., Nature (London) 323, S. 533-536，http://www.cs.utoronto.ca/~hinton/absps/naturebp.pdf

【3】The Forward-Forward Algorithm: Some Preliminary Investigations

G Hinton，https://bdtechtalks.com/2022/12/19/forward-forward-algorithm-geoffrey-hinton/

【4】https://news.cnstock.com/industry,rdjj-202403-5207288.htm

（本文首发于微信公众号“知识分子”）