第四章∶再回到分形龙

两人一看，张三本子上画的是下面的图形∶

图（4.1）∶谢尔宾斯基三角形

张三介绍说，这是另一种很简单的分形，由波兰数学家瓦茨瓦夫·谢尔宾斯基（Wacław Franciszek Sierpiński，1882-1969）而得名。谢尔宾斯基主要研究的是数论、集合论及拓扑学。他共出版了超过700篇的论文和50部著作，在波兰的学术界很有威望。

图（4.2）∶纪念谢尔宾斯基而发行的邮票和谢尔宾斯基奖章

张三说，他原来怎厶也想不通维数为什厶会是一个分数？後来，谢尔宾斯基三角形的生成过程使他有点开窍！

你们看，这个分形可以用两种不同的方法产生出来∶一种就是图（4.1）那种‘去掉中心’的方法∶最开始的第一个图形是个涂黑了的三角形，显然是个2维的图形。我们对它做的迭代变换就是挖掉它中心的三角形，成为第二个图，然後，再继续挖下去┅┅

“开始我想，无论怎厶挖，不都应该还是好多好多2维的小三角形吗？所以图形总是2维的┅┅”张三说∶“但後来，我在网上发现有另外一种方法，也能构成谢尔宾斯基三角形┅┅”

张三在本子上翻出另一张图给朋友们看∶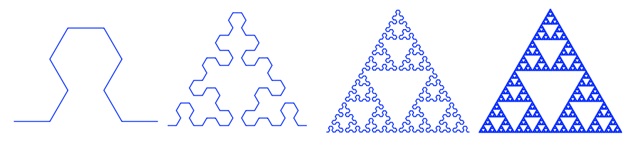

图（4.3）∶由曲线的迭代生成谢尔宾斯基三角形

这种方法是从图（4.3）中（1）所示的曲线开始迭代，迭代无限次之後，最後也得到谢尔宾斯基三角形。而曲线是一维的，按照张三原来那种经典的想法，谢尔宾斯基三角形好像又应该是1维图形。所以张三发现∶有些图形的维数不好用原来那种经典的方式来理解，当进行无穷次迭代後，几何图形的性质发生了质变，维数也不同于原来的生成图形的维数了。看起来，谢尔宾斯基三角形的维数应该是一个介于1和2之间的数。但到底是多少呢？张三看见李四给出了一个计算分形维数的公式，便急于想要把这个分数算出来。

根据李四所解释的方法，张三从图（4.1）或图（4.3）右边的最後一个图计算分形维数。你们看∶将图形按照2∶1的比例缩小，然後，用3个小图放在一起，就可以构成和原图一模一样的图形。因此，张三很快地算出了谢尔宾斯基三角形的豪斯多夫维数 d = ln(3)/ln(2) ≈ 1.585。

下面，我们再回头研究分形龙的维数。第一章的图（1.3）描述了分形龙的自相似性。从图中看出∶如果将分形龙曲线，尺寸缩小为原来的一半之後，得到右上图的小分形龙曲线。然後，将四个小分形龙曲线，分别旋转方向，成为如右下图的位置。最後，再按照右下图中箭头所指的方向，移动四个小分形龙曲线，便拼成了左下图的、与原来曲线一样的分形龙曲线。因此，如此可以证明，分形龙曲线的豪斯多夫维维数为2，因为根据公式（3.1），d = ln(4)/ln(2) = 2。

这儿又给出了一个具体例子∶经过无穷次迭代之後，图形的性质发生了质变，豪斯多夫维从1维变成了2维。也就是说，图（4.4）中，有限次迭代中的折线，无数次折叠的结果，使折线充满了2维空间，成为图中右边的2维图形。

图（4.4）有限次迭代到无限次迭代∶维数从1变成了2

有趣的是，如图（4.5）所示，分形龙图形的边界也是一个可以用迭代法产生的分形，现在我们来计算分形龙边界的豪斯多夫维。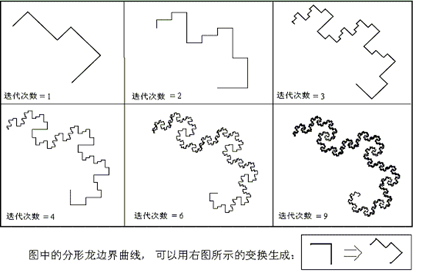

图（4.5）∶分形龙边界腹成的分形

由图（4.5）可知，整个分形龙曲线的边界是由四段相似的图形组成的。这种分形的维数估算方法比较复杂一些，它的“分形维数“(d)可以通过解如下方程求得:

图（4.6）∶分形龙边界由四段自相似图形腹成

通过分形龙及其它几种简单分形，我们认识了分形，理解了分数维。分形几何是理解混沌概念及非线性动力学的基础，在现代科学技术中，有着广泛的应用。

下面的连接可以让你亲身体会分形龙图形的趣味和美妙∶

http://www.tianfangyetan.net/cd/java/fractals.html

上一篇∶什麽是分数维？

返回目录

下一篇∶ 大自然中的分形