| 第二十一章﹕萬變中的不變 倍周期分岔現象的另一個重要特性是普適性。 除了生物群體數的變化之外,倍周期分岔現象還存在於其它很多非線性系統中。系統的參數變化時,系統的狀態數越來越多,返回某一狀態的周期加倍又加倍,最後從有序走向混沌。比如物理學中原來認為最簡單的單擺,也暗藏着混沌魔鬼,當外力加大時,新的頻率分量不斷出現,擺動周期不斷地加長,最後過渡到混沌;由美國華裔學者蔡少棠首先研究的混沌電路是倍周期分岔的又一個例子;此外,在金融股票市場,以至於社會群體活動中,都有魔鬼的身影,也有伴隨着的倍周期分岔現象。 到處都有倍周期分岔,以及接踵而至的混沌魔鬼,這是普適性的定性方面。普適性的另一個方面,定量方面,則與分岔的速度有關。 “分岔的速度?我注意到了,是越來越快的……”說話的是討論小組中的一個年輕新面孔,看起來像是個十五、六歲的中學生,王二介紹說這是林靈的弟弟林童,今年計算機系從高一學生中破格錄取的新生。林童看上去年輕,說話倒挺老練的,而且懂得的知識不少,確實是個小靈童。他指着圖(20.4)上面那張倍周期分岔圖給大家看。 圖中顯而易見,分岔的速度的確越來越快,相鄰兩個岔道口之間的距離越來越近。 “而且……”小靈童滿臉通紅,在這麼十幾個大哥哥大姐姐面前,說話時略顯尷尬,欲言又止,不過,在林零眼神的鼓勵下,他繼續說下去,越說越流利: “這個圖……分岔的速度雖然越來越快,但增快時卻似乎遵循某種規律,就有點像重力場中的自由落體。在中學物理課中學牛頓定律時,那兒有個g,叫做重力加速度。牛頓看見蘋果掉下來,下落的速度越來越快、越來越快……但是,速度增加的比例卻是相同的!也就是說,自由落體的速度變快了,但加速度g卻是不變的。並且,g的數值對任何下落的物體都一樣,它還與萬有引力常數G有關。所以,我就覺得,這個看起來層層相似的分岔圖中也可能有個什麼不變的東西吧。後來,到網上一查,果然如此!原來在倍周期分岔圖這兒也有兩個普適常數,分別叫做d和a,發現它們的人是費根鮑姆……” 米切爾·費根鮑姆(Mitchell Jay Feigenbaum,1944-)是美國數學物理學家。父親是波蘭移民,母親是烏克蘭人。青少年時期的費根鮑姆默默無聞,也未曾表現出任何所謂天才或神童的氣質。但是,他喜歡思考、迷戀物理。博士畢業後,因為找不到一個好的固定工作而四處奔波了好幾年。後來,終於在30歲時就職於新墨西哥州的洛斯阿拉莫斯國家實驗室。洛斯阿拉莫斯實驗室是美國兩個研究核武器的主要實驗室之一,二戰時期的曼哈頓計劃就在這兒進行。70年代,那兒養了一大堆的物理學家及別的相關學科的技術人員,工資不低,研究經費也不少,既沒有教學任務,也沒有要及時趕出成果發表論文的壓力。費根鮑姆在那兒悠哉游哉地如魚得水,儘管他當時在學術界還是一個無名小卒,只發表過一篇論文,科研成果寥寥無幾,但在他的理論部同事中間卻頗有聲名。一是因為他腦袋中經常冒出一些古怪的想法,打扮也有些不合潮流,滿頭捲曲的披肩長發使他看起來像個古典音樂家。費根鮑姆出名的另外一個原因,是因為他的知識淵博,深思熟慮過很多問題,無形中已經成為了同行們有難題時的特別顧問。 他所在研究小組的課題是流體力學中的湍流現象,費根鮑姆需要研究的是:威爾遜的重整化群思想是否可以解決湍流這個世紀老難題。 開始時,費根鮑姆似乎並不十分鐘情於研究小組的這個課題,不過,因為湍流看起來一片混亂,有些像那兩年科學界人士熱衷的“混沌”,這個研究方向使得費根鮑姆了解並熟悉了氣象學家洛倫茨宣告的“蝴蝶效應”,以及邏輯斯蒂迭代時產生的混沌問題。 費根鮑姆對邏輯斯蒂方程的研究獨立於羅伯特·梅。那年,他得了一個能放在口袋裡的HP65計算器,一有空閒,他便一邊散步、一邊抽煙,不時地還把計算器拿出來編寫幾句程序,研究令他着迷的邏輯斯蒂倍周期分岔現象。  圖(21.1):費根鮑姆和他的HP-65計算器 現在看起來十分簡易、當時售價為795美元的HP-65是惠普公司的第一台磁卡-可編程手持式計算器,用戶可以利用它編寫100多行的程序,還可將程序存儲在卡上,對磁卡進行讀寫。這在上世紀70年代已經顯得很了不得,因而,HP-65的綽號為“超級明星”。 當“超級明星”和美國宇航員一起登上阿波羅進入太空的時候,在新墨西哥州洛斯阿拉莫斯邊遠山區的費根鮑姆則用它來與邏輯斯蒂系統中的混沌魔鬼打交道,探索魔鬼出沒的規律。費根鮑姆喜歡寫點小程序,用計算來驗證物理猜想。早在十幾年前的大學時代,首次使用電腦時,他就在一小時之內寫出了一個用牛頓法開方的程序。 這次,費根鮑姆感興趣的是邏輯斯蒂分岔圖中出現得越來越多的那些三岔路口。他用計算器編程序算出每個三岔路口的坐標,即k值和相應的x無窮值。畫在紙上,構成了圖(21.2)中的左圖。 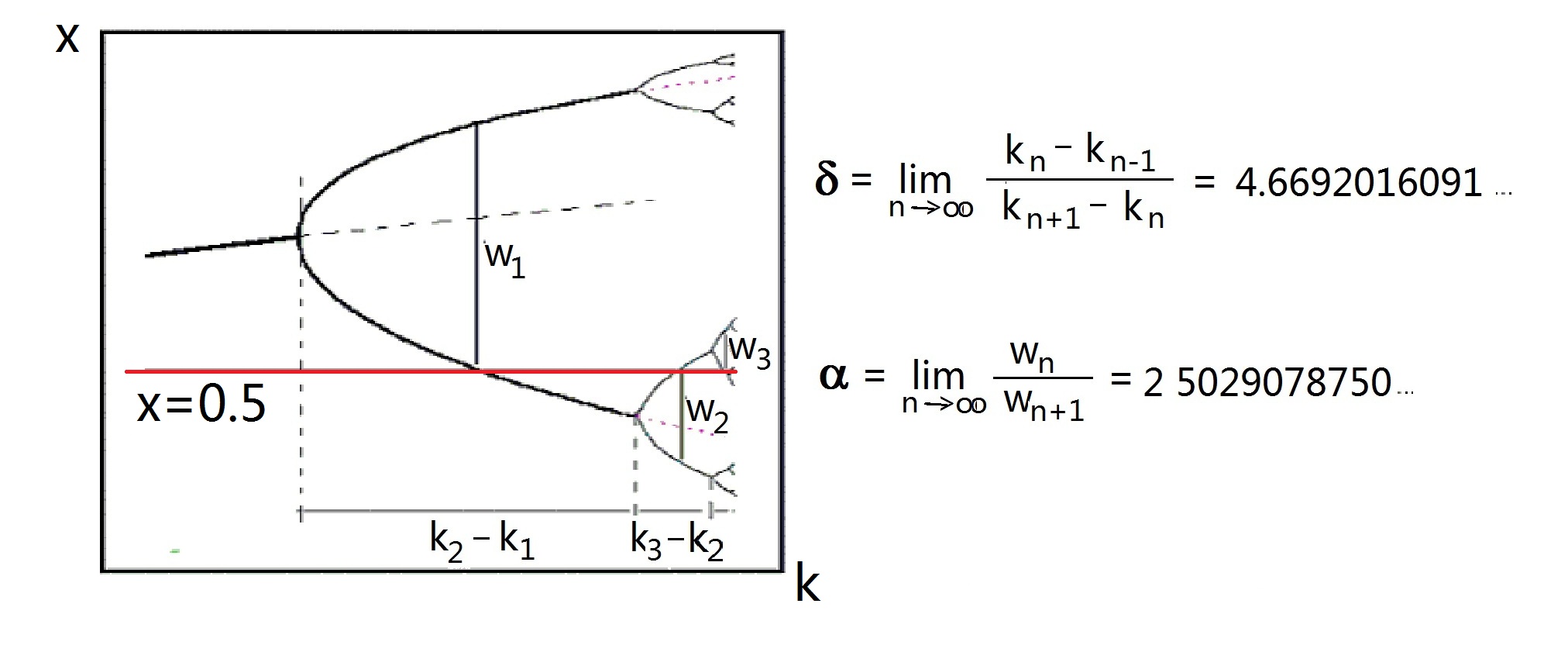
圖(21.2):費根鮑姆常數 和林童一樣,費根鮑姆也注意到了隨着k的增大,三岔路口到來得越來越快,越來越密集。從第一個三岔口k1開始:k1=3,k2=3.44948697, k3=3.5440903, k4=3.5644073,k5=3.5687594……。僅僅從k的表面數值,費根鮑姆沒有看出什麼名堂,於是,他又算出相鄰三岔路口間的距離d: d1 = k2-k1 = 0.4495..., d2 = k3-k2 = 0.0946..., d3 = k4-k3 = 0.0203..., d4 = k5-k4 = 0.00435... 從這些d之間,費根鮑姆好像看出點規律來啦!每次算出的下一個d,都大約是上一個d的五分之一!當然,並不是準確的五分之一,而是比例值差不多!好像有個什麼常數在這兒作怪,多計算幾項看看吧: d1/d2 = 4.7514, d2/d3 = 4.6562, d3/d4 = 4.6683, d4/d5 = 4.6686, d5/d6 = 4.6692, d6/d7 = 4.6694…… 你們看,上面列出的這些比值都很接近,但又並不完全相同,兩個相鄰比值之間的差別卻越來越小。費根鮑姆再計算下去,又多算了幾項後,便只能得到一樣的數值了,因為計算器的精度是有限的啊。於是,費根鮑姆便作了一個猜測,這個比值,(kn-kn-1)/(kn+1-kn)當n趨於無窮時,將收斂於一個極限值: d = 4.669201609…… 同時,費根鮑姆也注意到,分岔後的寬度w也是越變越小,見圖(21.2)中所標示的w1、w2、w3等等(這個寬度從x=0.5測量,圖中的紅線)。那麼,它們的比值是否也符合某個規律呢?計算結果再次驗證了費根鮑姆的想法,當n趨於無窮時,比值wn/wn+1將收斂於另一個極限值: α= 2.502907875…… 啊,原來這個分岔圖中隱藏着兩個常數!費根鮑姆深知物理常數對物理理論的重要,一個新概念、新理論的誕生往往伴隨着新常數的出現,比如牛頓力學中的萬有引力常數G,量子力學中的普朗克常數h,相對論中的光速c……諸如此類的例子太多了。新常數的發現也許能為新的革命性的物理理論打開新窗口。想到這兒,費根鮑姆欣喜若狂,立即打電話給他的父母,激動地告訴他們他發現了一些很不平凡的東西,他可能要一鳴驚人了。 上一篇∶魔鬼不穩定 返回目錄 下一篇∶再回魔鬼聚合物 | 