《明捷数学随谈(3):张益唐一鸣惊人》 By 明捷 【八.孪生素数猜想和张益唐】 2013年的一天,海外各华语媒体突然爆出一个新闻,一个叫张益唐的人解决了一个古老的数论难题:孪生素数猜想。论文发表在美国最权威的数学期刊上。张益唐是何方神圣?即使是数学届人士也很少有人听到过这个名字。仔细读一下报道,人们发现这里面有一个曲折的人生故事。 
孪生素数猜想是什么时候,由什么人提出的,都不清楚。但其历史比同样著名的哥德巴赫猜想要久远的多。除了1以外,自然数按整除性可分为两类,其中一类数可以被更小一些的数整除,如4可以被2整除,6可以被2和3整除,等等。这一类数被称为合数。另一类数除了自身和1以外,不能被任何其它数整除,称为素数(也称质数),如2,3,5,7等是素数。显然,合数可以表示为若干素数的乘积,如6=2×3,9=3×3,等等。偶数中除了2以外,其它都是合数。而奇数则有可能是素数,也有可能是合数。早在公元前,古希腊的数学家就对素数产生了很大的兴趣。他们发现,随着数字的增大,素数变得越来越稀薄。比如100到200之间的素数比1到100之间的少,而1000到1100之间的素数要少得更多。会不会数字增大到某个值后,素数就消失了呢?如果是这样,自然界的素数是有限的,为稀缺数。公元前300年,著名的希腊数学家欧几里得用反证法,简洁而漂亮地证明了素数有无限多个。 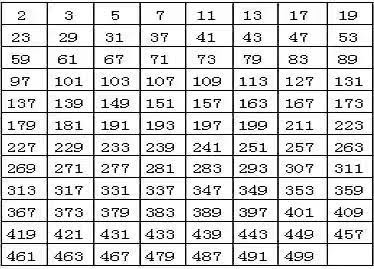
(500以内的素数表) 欧几里得首先假定只有n个素数,设为A1,A2,…,An。将这n个素数乘起来,再加上1,得到A=(A1×A2×....×An)+1, 显然,这个A比A1,A2,…An都要大,根据假设,它只能是合数。但另一方面,A显然是个素数,因为它不能被任何一个素数整除。这就说明一开始假设素数为有限个是不对的,因此素数的个数是无限的。 很早的时候,人们就发现,有些素数是成对出现的,每对素数的差为2。例如(3,5),(5,7),(11,13),(17,19)等等。于是人们很自然地想到,像这样相差为2的素数对会不会有无穷多个呢?这就是所谓的孪生素数猜想。和验算哥德巴赫猜想一样,可以一直验算下去,找到很多个这样的素数对,但不能找到无穷多个。因此,这不能算做证明。这其实是所有数论难题中的症结所在,即如何从有限过渡到无穷。欧几里得用反证法轻而易举地解决了素数个数无穷多的命题。然而很多与素数相关的命题却不能这么幸运地得到到证明,必须用到高等数学分析的工具,将离散问题转换为连续问题,从有限过渡到无穷。 张益唐在美国《数学年刊》上发表的文章,证明了存在无穷多个素数对,每对数的间距是有限的,他给出的这个有限的间距为7000万。也许你会说,孪生素数猜想不是说每个素数对间距为2吗?这个7000万相差十万八千里,怎么能说解决了这个问题呢?据行家说,张取得的进展是决定性的,剩下的工作是体力活,将7000万缩减到2只是时间问题。打个比方,你要去探访某座城中的一户人家,这座城的城门在很长时间内都是紧闭的,没人能打开。现在你用一个方法把城门打开了,进了城,离那户人家还有段距离,但走过这段距离是早晚的事。张的文章发表不久,天才数学家陶哲轩很快就将素数对的间距从7000万缩小到1000以内。 
张益唐证明孪生素数猜想时,已经58岁了,他当时是新罕布什尔大学的一个讲师。在美国,大学讲师的职位是临时的,只负责教课,没有科研任务。在这之前二十多年,张只在专业期刊上发表过一篇文章,数学界大多数人都没有听说过他的名字。这是怎么回事呢?后来纽约时报刊登了一篇文章,报道了张益唐的故事。其它媒体也作了跟踪报道。有人形容这是一个谦卑的人生故事(a humble life story)。 张益唐出生于1955年。1978年,他考入北京大学数学系。和很多77,78级大学生一样,张当时不是高中应届毕业生,上大学前他在北京当过几年工人。张在大学期间学习成绩一直名列前茅,后来他跟从潘承彪教授读研究生,专业方向是数论。1985年,张益唐赴美,到普渡大学跟从代数学专家莫宗坚教授读博士。代数学不是他的兴趣所在,但张仍然选择研究该领域一个著名的世界难题:雅可比猜想。几年后,张发表论文称他解决了雅可比猜想,但随后被人发现是错的,这个错误追溯到他所引用的莫宗坚的一篇论文,那篇论文被发现是错的。这本来也正常,此前很多证明雅可比猜想的论文都被发现是错的。但莫宗坚对此很恼火,这事导致张在博士毕业后找工作时得不到莫的推荐信。 
在美国,博士毕业若想在学术圈找工作,一定需要导师的推荐信。得不到莫的推荐,张到学术界发展的路被堵死了。那段时间正赶上前苏联解体,大批数学家和理论物理学家到美国求发展,有的进了学术界,有的到华尔街搞金融分析。一时间僧多粥少,一职难求。这意味着张益唐的职业生涯还没有开始就结束了。他曾考虑过回国,但因故未能成行。接下来的若干年里,张益唐辗转各州,靠在餐馆,旅店打工谋生。在打工生涯的同时,张在工余时间开始了对孪生素数猜想的研究。由于他博士期间的专业方向不是数论,他得花很多时间补习一些必要的数论知识,了解该领域的最新发展。另外,他对西方古典音乐和文学有着浓厚的兴趣,这些在他落魄的日子里,支撑着他的生活。 张的一些同学和朋友时不时地会给他帮助。一个朋友见他一直未成家,就决定给他介绍一个对象。有一天请他到纽约的一家中餐馆进餐。酒至半酣,一位女服务员走近前来,朋友问他觉得这位女士如何,他说了几句好话。几天后,朋友再次请他吃饭,那位女士也在座,后来就成了他的太太。张在北大的一个师弟后来到新罕布什尔大学数学系做了教授,在这个师弟的引荐下,张谋得了新罕布什尔大学的一个讲师职位,从此有更多的时间从事他的研究。在张致力于孪生素数猜想的那些年期间,美国的一些数论专家曾开过一个研讨会,讨论孪生素数猜想,结果认为,目前解决该猜想的条件还不具备,建议学术界暂缓对该猜想的研究。张益唐没有资格参加这个会议,对会议决定一无所知,这对他其实是件好事,可以埋头继续他的研究。 
2012年的圣诞节期间,张益唐到一个朋友家里做客,听说时常有鹿会光顾这家人的后院。一天下午,他独自一人到后院,希望能碰到鹿,同时他仍然想着问题。突然一个想法闪现,他知道问题有望解决了。随后他把这个想法写了下来,完成了一篇论文,寄到权威的《数学年刊》。通常在这个杂志上发表论文需要等两年的时间,但张的论文一个多月后就发表出来了。此后,张益唐要他太太留意一下这段时间的中文媒体。一段时间后,张益唐的名字遍布了海外各大中文媒体。这时他太太对他说,你现在出名了,以后把头发梳整齐点。 
在一篇张益唐访谈中看到下面这段对话: “数学家需要什么天分吗?” “专注”,“而且,永远不要放弃你的个性”。张益唐说:“也许你面对的东西非常复杂,需要很长时间,但你应能依据直觉挑出重要的部分。” “你觉得你聪明吗”? “可能有一点吧。”他回答道。 
2013年在台湾接受数学家季理真采访时,张益唐曾这样强调:“勤能补拙。我根本不觉得我这个人有多聪明,但我有足够的勤奋,这是我能说的忠告。” 哈代在他的书里说:“一个数学家可能到60岁时还能胜任,但不要期望他会有原创性想法。” “这句话可能不适用于我。”张益唐说,“我觉得我仍然富有直觉,我仍然对自己有信心,我仍然还有其他的期许。”“我还有两三个问题要解决,”他说,“素数的有界距离很成功,但我还有别的问题要干。” “和素数分布同样重要吗?” “是的,同样重要。” (照片来自于网络,感谢)
| 