1最早的数学 数学有着久远的历史。从原始社会开始,人类就在绳子上打结,以便记数;在地上画图,测量大小。“结绳记数”开创和发展了数字的最早概念,“土地测量”等生产活动的需求,使几何学应运而生。 如今找到最多最早数学记录的地方,是古埃及和巴比伦。目前最古老的数学文本是《普林顿 322》(古巴比伦,约公元前1900年),《莱因德数学纸草书》(古埃及,约公元前2000年-1800年),以及《莫斯科数学纸草书》(古埃及,约公元前1890年)。 
图1:普林顿 322泥板 以上古文本中,都有关于几何最早的记录。如图1所示的古巴比伦的普林顿 322是一块泥板,上面的表格列出了不少勾股数,也就是满足a2+b2=c2的a、b、c的正整数集合,比希腊、中国、印度的数学家等等的发现,要早上一千多年。 
图2:莱因德数学纸草书 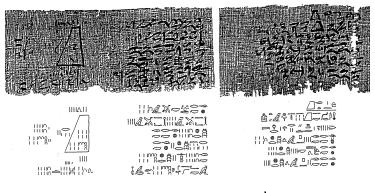
图3:莫斯科数学纸草书 现藏大英博物馆的“莱因德数学纸草书”,总长525厘米,高33厘米,与保留于俄罗斯莫斯科普希金造型艺术博物馆的“莫斯科数学纸草书”齐名,是最具代表性的古埃及数学原始文献。两本纸草书中都有不少几何问题,据说其中有对π的简单计算,所得值为3.1605。 古埃及和巴比伦距今已将近4000年,应该算是人类最早期的数学。但是,两地的资料有限,人物不详。因此,追溯数学历史之源,还是从古希腊开始比较合适。 2古希腊的天时地利人和 当今世界的人口超过70亿,根据人类演化历史的研究及现代DNA技术的追踪,这几十亿的人口,却是来源于一个共同的祖先:非洲人。 后来,人类的祖先以双脚走出非洲遍游世界,将后代延续繁衍到地球各处。再更进一步,人类逐渐沿河而居,聚集在一起建立了城市和国家,并因之而独立诞生了好几个所谓的“文明古国”,其中包括公元前3500年左右的两河文明、公元前3000年时尼罗河畔的埃及文明、恒河流域的古印度文明(公元前2500年左右)、以及公元前2000年左右黄河长江流域的中国华夏文明。 尽管多种人类文明独立诞生于不同的地区,各自特色不一,但是,作为人类文明思想精华之一的“科学”,却又只是起源于唯一的一个地方:古希腊! 科学之起源与数学思想的发展密切相关,如今被称为人类第一位数学家的先贤叫泰勒斯(Thales,公元前624年-公元前546年),或称“米利都的泰勒斯”。米利都是泰勒斯的家乡,见图4。 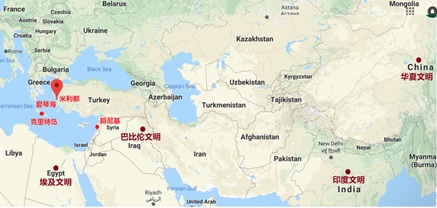
图4:文明古国,数学及科学的诞生 那么,科学为何独独诞生于古希腊而非别处?答案有些出乎人们的意料之外,其原因竟然与古希腊的地理环境有关! 事实上,公元前500-600年左右,人类几大古文明世界不约而同地出现了一段兴旺场面:思想家辈出,哲学派别林立,各具特色和风格。然而同时,随着各方宗教思想的严密化和系统化,东西方哲学思想开始分道扬镳。这就是被后人称为“轴心时代”的年代,被描述为是人类文明历史上“最深刻的分界线”。 那段时期,中国有孔子、老子、墨子、庄子、列子等诸子百家,印度有释迦牟尼,诞生了佛陀,古代波斯出现了拜火教……人类的几大古文明社会开始通过不同的哲学反思来认识和理解这个世界。 大多数这些文明古国都始于农业的发展,建立于江河流域,而古希腊并不具备这种条件。例如泰勒斯的家乡米利都位于爱琴海东部沿岸,属于古希腊爱奥尼亚诸岛一带。那儿没有河流只有海洋,没有平原只有山地。 因此,古希腊一不傍河,二无森林,既未发展出如文明古国那种农业文明,也不可能有像玛雅文化那样的丛林文明。 然而,古希腊却自有其“天时地利人和”之处!特殊的地理环境,使它尽管没有“原生文明”,却孕育出了一种独一无二的、崇尚自由思想、有着海洋色彩的“次生文明”。 米利都位于多山的爱奥尼亚一带,沿岸是一个一个的出海口。它们多面环山一面朝海,内路为群山所阻,海道却极为便利。高山阻隔使它们互相独立,海道畅通有利于发展自由的商业贸易。因此,这些出海口便形成了一连串以航海为基础的,颇为富裕和自治的、相互没有依附关系的独立城邦,米利都便是当时较大的12个城邦之一。 爱琴海一带,与米利都城邦隔海相望的,南是古埃及,东有巴比伦。频繁兴旺的商业活动不时带来这两个文明古国的相关信息,而这两个文明又时常感受到更远的印度及华夏东方文明。因此,“轴心时代”温暖的春风,也就这样间接地飘进了古希腊。 古希腊的思想家们,在多方文明的环绕渗透下,既保持其特有的自由思想,又包容地大量汲取外来的养分,最终化劣为优扬长避短,导致科学发端于古希腊。 著名物理学家薛定谔曾经将其原因大致归纳为如下3点: a、古希腊的小城邦,实行的是类似于共和制的政治; b、航海贸易刺激经济,商业交换促进技术,由此而加速思想交流,科学理论形成; c、爱奥尼亚人大多不信教,没有像巴比伦和埃及那样的世袭特权的神职等级,有利于倡导独立思想新时代的兴起。 科学脱胎于哲学,得益于数理。古印度哲学多探讨人与神的关系;中国哲学家们多热衷于研究如何安国兴邦平天下,探讨的是人与人的关系。唯独古希腊哲学家们,喜好研究自然本身的规律,探讨的是人与自然的关系,使得古希腊哲学思想独具一格。 人与自然的关系,正是科学的本质,其中缺不了数学。 3第一位数学家何许人也? 古希腊数学家泰勒斯(Thales,公元前624年-公元前546年),被誉为世界第一位数学家、哲学家、科学家。泰勒斯对科学作了哪些贡献?本文重点谈他对数学的贡献。 泰勒斯证明了“泰勒斯定理”,首开先河引进“证明”的思想,将数学从经验上升为理论,继而使理性精神发源于古希腊,之后又传播到欧洲并催生了宏伟的现代科学… 
图5:米利都的泰勒斯 泰勒斯出生于米利都,尽管当年这个城邦名义上属于波斯统治,但实际上具有很大的独立性。米利都的大多数居民,是在公元前1500年左右,从克里特岛迁来的移民。克里特岛在米利都的西南方,位处古埃及、巴比伦文明的辐射范围以内。而到了泰勒斯的父母一代,他们原是东南方向善于航海和经商的腓尼基人,也算是奴隶主贵族阶级。因此,天才的泰勒斯从小受到良好的教育。 泰勒斯早年随父母经商,曾游历埃及、巴比伦、美索不达米亚平原等地。泰勒斯兴趣广泛,涉及数学、天文观测、土地丈量等各个领域,游历过程中学习到很多知识。 泰勒斯最著名的哲学观点:水是万物之本。他研究天文,确认了小熊座,估量太阳及月球的大小,修定一年为365日。 数学上,他应用在埃及跟当地祭司学习的数学知识于测量:估算船只离岸的距离,从金字塔的阴影计算其高度,证明了泰勒斯定理。 泰勒斯是西方思想史上第一个有记载、有名字留下来的思想家。这位人称“科学之祖” 的伟大人物也在民间留下了很多趣闻逸事。 据说泰勒斯有一次用骡子运盐,一头骡子不小心滑倒溪水中,背上的盐被迅速溶解了一部分,于是这头狡猾的骡子每到一个溪水旁就打一个滚,故意让盐溶解负担减轻。泰勒斯发现了这点,便将计就计,有时让这骡子改驮海绵,骡子到溪边照样打滚,却发现负担越来越重。最后,聪明的泰勒斯终于使那头骡子改掉了溪边打滚的习惯,老老实实地继续驮盐! 泰勒斯还有几个预言成真的故事。他曾经预言有一年雅典的橄榄会丰收,并乘机购买了米利都所有的橄榄榨油机,抬高价格垄断了榨油行业,于是大赚了一笔,他以此证明自己如果把心思放在经商上,有潜力成为一个精明的商人。 据说泰勒斯利用他学到的天文知识,预测到了公元前585年的一次日食。这点可见于古希腊历史学家希罗多德在其史学名著《历史》中之记述: “米利都人泰勒斯曾向爱奥尼亚人预言了这个事件,他向他们预言在哪一年会有这样的事件发生,而实际上这话应验了。” 据说在那年,米堤亚和吕底亚的军队正准备打仗,泰勒斯的预言阻止了这场战争,因为古希腊人将日食视作上天将惩罚人类的一种警告,交战双方自然不愿违背天意,于是便签订了停战协议。根据现代天文学的知识,那是公元前585年5月28日的日食,泰勒斯应该无法准确地给出日期,只能预料一个大概的年月而已。 泰勒斯晚上没事时喜欢一边散步一边抬头看天象,也冥思苦想哲学问题,脑海中则免不了思绪翻滚腾云驾雾。但他只知研究天上的星星,却看不到自己脚下的大坑,有一次不小心掉进了井里,女仆听到叫喊声后,才好不容易将他救了上来。 4泰勒斯对数学的贡献 泰勒斯在数学方面作了不少工作,从具体实践到数学思想都有所贡献,下面一一道来。 4.1 实用计算 泰勒斯利用在埃及和巴比伦学到的几何学知识,发展了以几何物件的相似为基础,计算一些无法直接测量的高度或距离的方法和技巧。例如,其中包括的三角测量法,如图6所示。他借由测量自己及金字塔的影子长度,以及自己的身高,并运用相似形的原理来测量金字塔的高度。泰勒斯亦根据此原理推算自己与海上船只的距离,以及推算悬崖的高度。 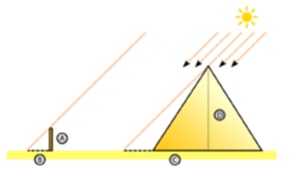
图6:泰勒斯从金字塔的阴影估算出金字塔的高度 图6中,A是木棍长度,B和C分别是太阳照射于木棍和金字塔所形成的阴影的长度。知道A、B和C,就可以计算出金字塔的高度D和阳光与地面的夹角。 泰勒斯也使用类似的方法,测量海上船舶与海岸之间的距离。 4.2 几何证明 泰勒斯在进行早期的几何研究中,确立了一些逻辑和几何真理。他通过演绎推理得出许多数学定理和命题。其中最典型的一个称为泰勒斯定理。 泰勒斯定理讲的是:“直径所对的圆周角是直角。” 泰勒斯并非此定理的首名发现者,古埃及人和巴比伦人一定已知这特性,可是他们没有给出证明。 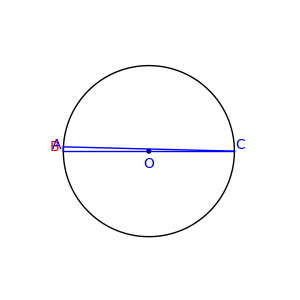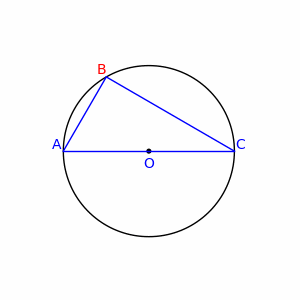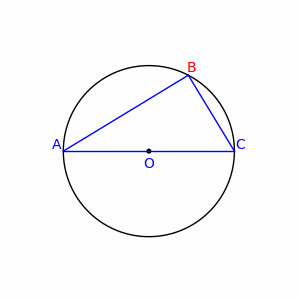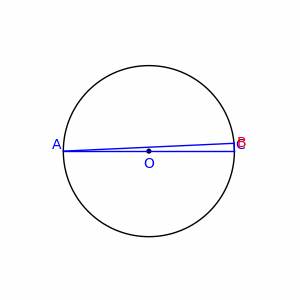
图7:泰勒斯定理 如图所示,AC是直径,其中点O便是圆心,在圆周上任取一点B,连接B和A、C。根据泰勒斯定理,无论B在哪里,角ABC都是直角。 为证明泰勒斯定理,需要以下两个事实: 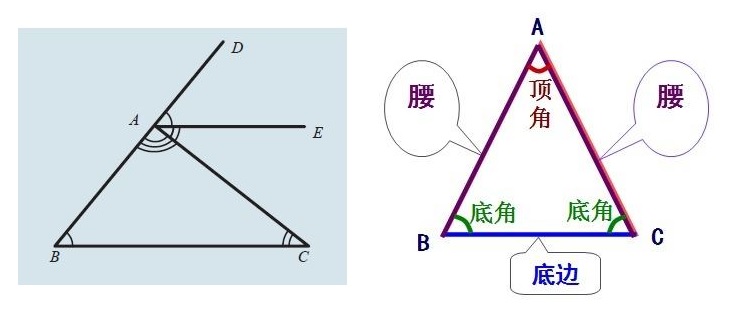
1. 三角形三个内角和是180°,2. 等腰三角形的底角相等。 图8:证明泰勒斯定理需要的两个命题 因为O是圆心,所以OA、OB、OC都是半径。圆的半径长度相等。所以三角形OAB和三角形OBC都是等腰三角形。我们把两个三角形的底角分别命名为α和 β。 讲ABC看作一个大三角形,所以: α + α + β + β = 180°, ⇒ 2 α + 2 β = 180°, ⇒ α + β = 90°。 所以角ABC是直角三角形。 在推导泰勒斯定理的同时,泰勒斯也证明了其他几个基本命题:圆被它的任一直径所平分,半圆的圆周角是直角,等腰三角形两底角相等,相似三角形的各对应边成比例,若两三角形两角和一边对应相等则两三角形全等。 4.3 理性精神 泰勒斯定理的证明是很容易的,属于初中平面几何的范围。但泰勒斯对数学的贡献不是在于几何证明本身,而是在于引进了“证明”的方法和概念。要知道,在泰勒斯之前,已经有一大堆几何事实,但没有过任何“证明”。泰勒斯是已知的第一个将演绎推理应用于几何的人,在一个充满谬误和迷信的时代,他是第一个用逻辑推理来理解这个世界的人,这就是为什么他被认为是第一位真正的数学家。 几何定理为什么需要被“证明”呢?至少有两个原因:一是通过证明,才能确认定理的普适性,例如泰勒斯定理说:直径所对的圆周角是直角,只有证明之后,才确定这儿指的是直径所对的“任何”圆周角,而不是特殊的某一个。第二个原因是,“证明”能够发掘几何事实相互之间的关系,发展逻辑推理的方法。 打个比喻说:未经证明的诸多几何事实,就像是混乱堆砌在一块儿的一堆砖头(见图9左)。而证明将它们互相关联起来,建造成宏伟的建筑物(见图9右)。 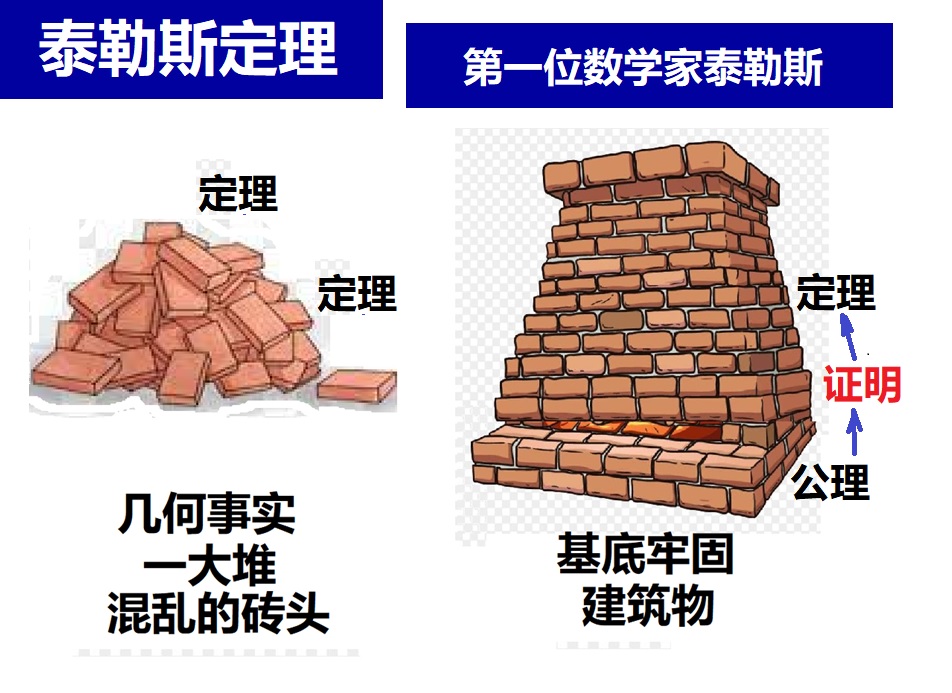
图9:逻辑推理和证明的意义 其它的文明,例如古埃及、巴比伦、印度、中国等,更早的时期就发现了很多的“几何事实”,都有早期数学知识的记载。但因为不强调形式逻辑,没有发展出演绎、证明、公理化等方法,因而未成大器。 泰勒斯首开先河的“理性精神”,是数学的精髓。 泰勒斯划时代的贡献是引入了证明的思想,将数学从经验上升到理论,这在数学史上是一次不寻常的飞跃。为毕达哥拉斯创立理性数学、欧几里德的公理化几何等奠定了基础。较之世界其他文明,这是古希腊独有的,使其成为数学乃至科学的奠基者。 5古希腊数学的启示 理性思维是走向科学的第一步。具体到中国,再次引用一下爱因斯坦论及科学为何没有起源于中国时所说的话: “西方科学的发展有两个基础:希腊哲学家发明的形式逻辑体系(如欧几里得几何),和文艺复兴时期发现通过系统实验找出因果关系的方法。” 简而言之,爱因斯坦是说,科学发源于古希腊文化,是基于两个必要条件:形式逻辑体系和系统实验。爱因斯坦强调的“形式逻辑”,正是中国人比较欠缺的。 中国人的思维方式基本上属于直观的形象思维,而西方人更重视逻辑思维。从逻辑学角度来看,中国人更偏向于辩证逻辑,而西方人更偏重形式逻辑。 辩证逻辑和形式逻辑各有所长,但是,形式逻辑是基础,走向辩证可算是锦上添花。缺乏形式逻辑的辩证会流于“狡辩”。换言之,中国人的思维方式有一定的缺陷,或者可以说,中国人的思维方法貌似辨证有余,但却独缺形式逻辑。 科学离不开数学,爱因斯坦的说法肯定了这点。而数学的内容不只是计算和证明,它也不仅是作为科学的语言和工具,更为重要的:数学是思想,是理性精神,是能给予科学精密性和严格性的形式逻辑。 中国古代并不是没有数学,而是没有基于精密思维的形式逻辑体系。中国人脑袋中也不乏解决具体数学问题的小技巧,但却缺乏大范围的数学思想。 所以,很有必要学习一点数学史,探索数学及科学的根本精神,方能逐步克服我们思维方法之不足。 ×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××× 本人的科普视频:YouTube: 天文航天:“談天說地” https://www.youtube.com/playlist?list=PL6YHSDB0mjBLmFkh2_9b9fAlN7C4618gK 趣味数学:數學大觀園 https://www.youtube.com/playlist?list=PL6YHSDB0mjBJifi3hkHL25P3K9T-bmzeA
也发在微信公众号“天舸”上(微信号:gh_e01fc368fe31): 
长按/扫一扫二维码,敬请关注我的微信公众号“天舸” !
××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
| 