

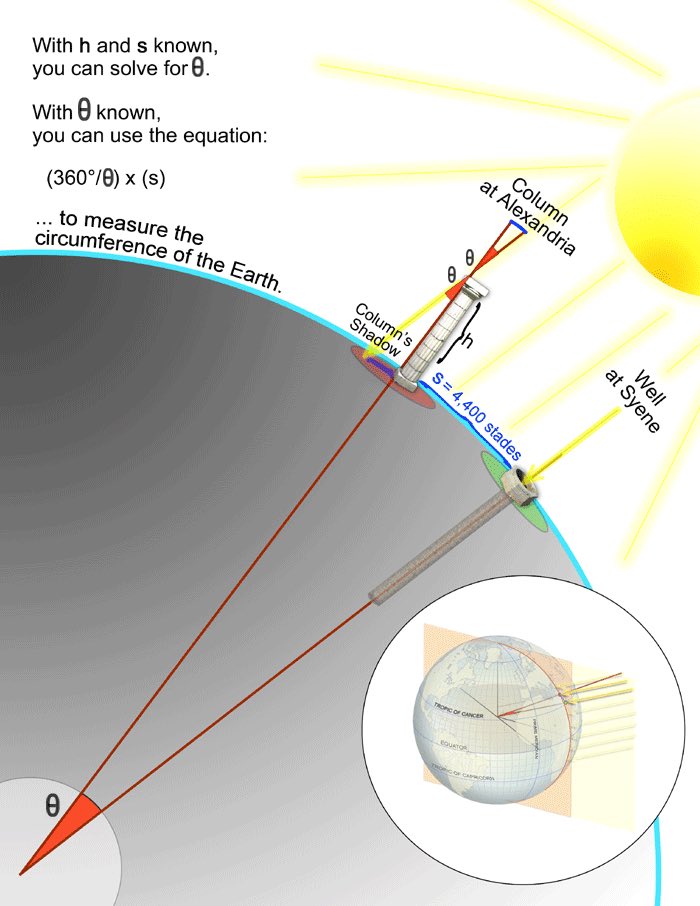
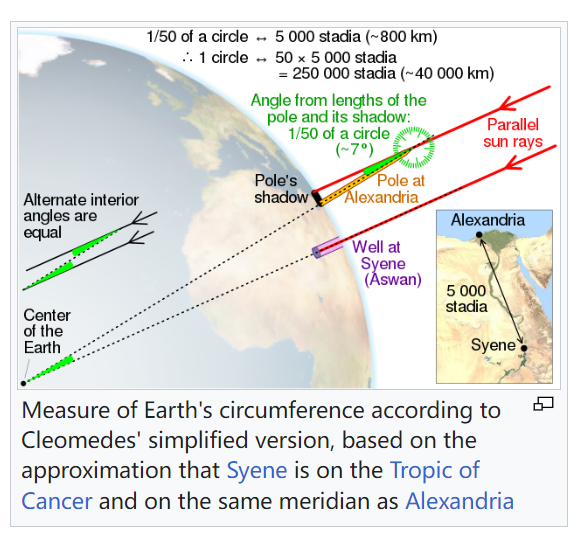
在 20 世纪中叶,我们开始向太空发射卫星,这将帮助我们确定地球的确切周长:40,030 公里。但在 2000 多年前,古希腊的一个人仅用一根棍子和他的大脑就想出了几乎完全相同的数字。以下是视频的文字记录。 古希腊数学家如何计算地球的周长。20 世纪中叶,我们开始向太空发射卫星,这将帮助我们确定地球的确切周长,即 40,030 公里。 但在 2000 多年前的古希腊,一个人通过将一根棍子插在地上得出了几乎完全相同的数字。这个人就是埃拉托色尼。希腊数学家,亚历山大图书馆馆长。 Eratosthenes 听说在亚历山大港以南的城市 Syene,夏至日中午没有垂直阴影投射。太阳直射头顶。他想知道亚历山大港是否也是如此。
So, on June 21 he planted a stick directly in the ground and waited to see if a shadow would be cast at noon. It turns out there was one. And it measured about 7 degrees. Now, if the sun's rays are coming in at the same angle at the same time of day, and a stick in Alexandria is casting a shadow while a stick in Syene is not, it must mean that the Earth's surface is curved. And Eratosthenes probably already knew that. The idea of a spherical Earth was floated around by Pythagoras around 500 BC and validated by Aristotle a couple centuries later. If the Earth really was a sphere, Eratosthenes could use his observations to estimate the circumference of the entire planet. Since the difference in shadow length is 7 degrees in Alexandria and Syene, that means the two cities are 7 degrees apart on Earth's 360-degrees surface. Eratosthenes hired a man to pace the distance between the two cities and learned they were 5,000 stadia apart, which is about 800 kilometers. He could then use simple proportions to find the Earth's circumference — 7.2 degrees is 1/50 of 360 degrees, so 800 times 50 equals 40,000 kilometers. And just like that, a man 2200 years ago found the circumference of our entire planet with just a stick and his brain.
于是,6 月 21 日,他直接在地里插了一根棍子,等着看中午会不会有影子。原来有一个。它测量了大约 7 度。 现在,如果太阳光线在一天中的同一时间以相同的角度射入,并且亚历山大港的一根棍子投射出阴影,而 Syene 的一根棍子则没有,这一定意味着地球表面是弯曲的。Eratosthenes 可能已经知道了。 球形地球的想法在公元前 500 年左右由毕达哥拉斯提出,并在几个世纪后被亚里士多德证实。如果地球真的是一个球体,埃拉托色尼可以利用他的观察来估计整个行星的周长。 由于亚历山大港和 Syene 的阴影长度差异为 7 度,这意味着这两个城市在地球 360 度表面上相隔 7 度。Eratosthenes 雇了一个人来测量两个城市之间的距离,并得知它们相距 5,000 stadia,即约 800 公里。 然后他可以使用简单的比例来计算地球的周长——7.2 度是 360 度的 1/50,所以 800 乘以 50 等于 40,000 公里。就这样,2200 年前,一个人只用一根棍子和他的大脑就找到了我们整个星球的周长。


该视频由 Alex Kuzoian 制作。 该视频最初发布于 2016 年 7 月 3 日
https://www.businessinsider.com/how-greek-eratosthenes-calculated-earth-circumference-2016-6#:~:text=Eratosthenes%20hired%20a%20man%20to,times%2050%20equals%2040%2C000%20kilometers.

https://weibo.com/2099300141/KDgEgaz9X?layerid=4693587922518437
Earth's circumference is the distance around Earth. Measured around the Equator, it is 40,075.017 km (24,901.461 mi). Measured around the poles, the circumference is 40,007.863 km (24,859.734 mi).[1]
地球的周长是地球周围的距离。 围绕赤道测量,为 40,075.017 公里(24,901.461 英里); 围绕两极测量,为 40,007.863 公里(24,859.734 英里)。


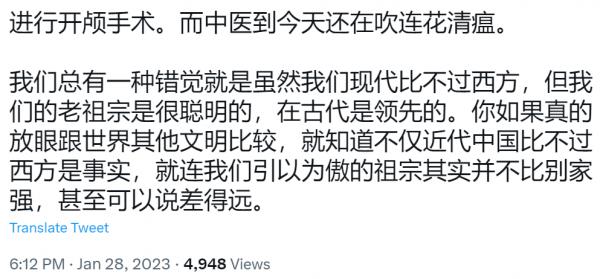

https://twitter.com/tankman2002


https://blog.creaders.net/u/8994/202301/454343.html



|
