| 第二十四章﹕孤立子的故事 孤立子是非线性研究的另一个热点。 第一次发现水波中产生的孤立子现象,距今已经有将近180年了。那是1834年8月的一天,在苏格兰爱丁堡市附近的尤宁运河岸边,26岁的造船工程师约翰·司科特·罗素骑马观察船在河中的运动情形时发现的。 之后,罗素这样描述他那天的惊人发现【1】: “我正在观察一条船的运动,这条船沿着狭窄的河道由两匹马快速地曳进。当船突然停下时,河道中被推动的水团并未停止,它聚积在船首周围,剧烈翻腾。突然,水团中呈现出一个滚圆光滑、轮廓分明、巨大的、孤立耸起的水峰,以很快的速度离开船首,滚滚向前。这个水峰沿着河道继续向前行进,形态不变,速度不减。我策马追踪,赶上了它。它仍以每小时八、九英里的速度向前滚动,同时仍保持着长约三十英尺、高约一到一点五英尺的原始形状。后来,我追逐了一两英里后,才发现它的高度渐渐下降。最后,在河道的拐弯处,我被它甩掉了。” 这一“奇特的”、“美丽的”、孤立的水峰令年轻的罗素着迷,而且,他敏感地意识到,自己发现了一个新的物理现象。罗素的直觉不无道理,他是一个经常在河边进行观察和研究的造船专家,成天与水流水波打交道,因此,他坚信这个现象与一般常见的水波截然不同,一般水波是很快就要弥散、消失的,维持不了这么久。此外,罗素也是一个训练有素的船舶设计师,有深厚的物理数学功底,他相信,那时现有的波动理论,包括牛顿的理论和伯努利的流体力学方程,都没有描述过,也无法解释他看见的这种奇特现象,因此,罗素给自己的发现取了个新名字:平移波。后来被学界命名为孤立子,或孤子。 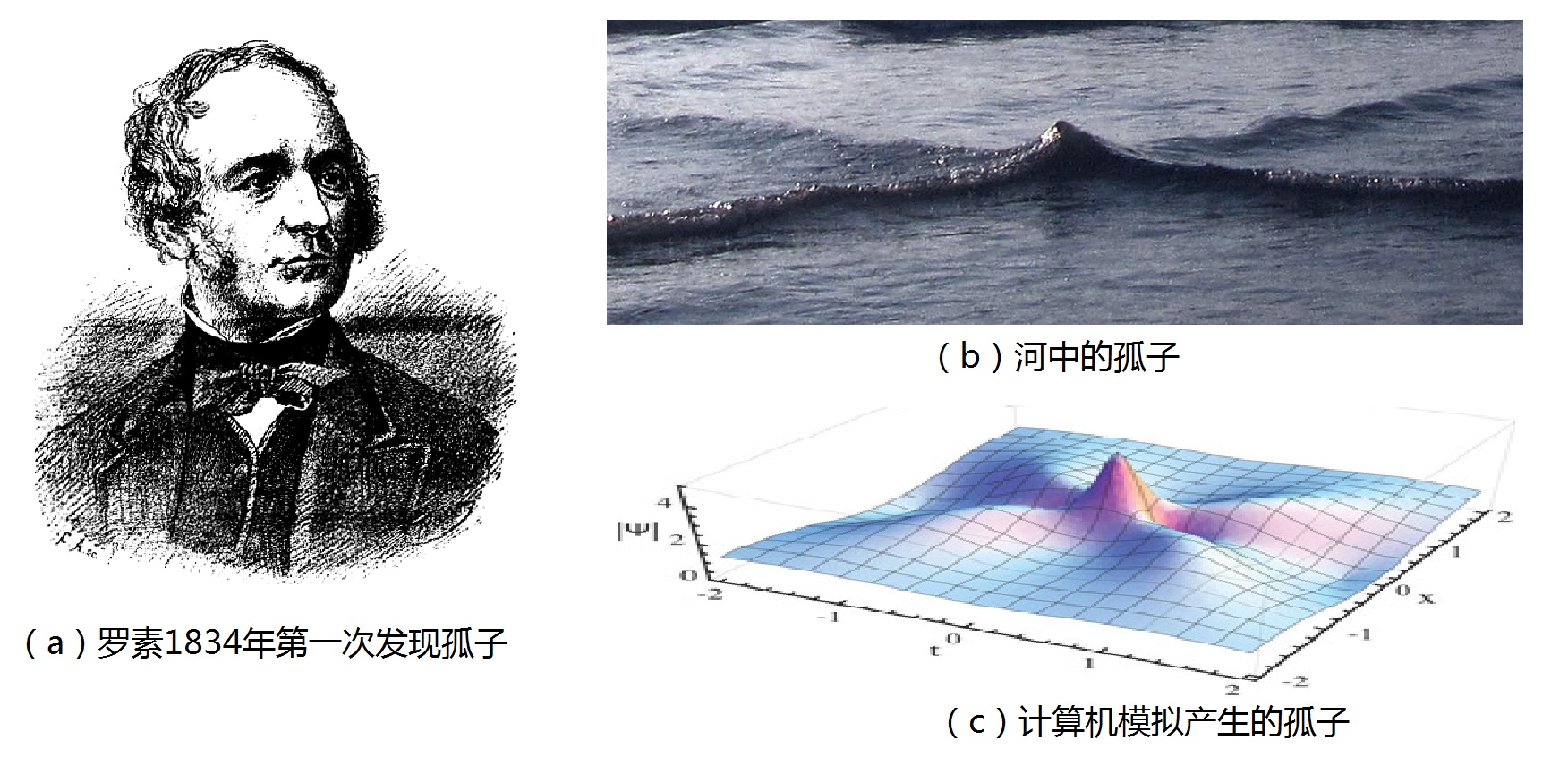 图(24.1):(a)罗素在1834年第一次观察到孤子(平移波); (b)水波中的孤立子现象Phys. Rev. E 86, 036305 (2012); (c)计算机模拟所产生的KDV方程孤立子解【2】 偶然发现的‘平移波’在罗素的脑海中久久挥之不去,为了深入研究这个现象,罗素在自家后院里建造了一座宏大的实验水槽,并且他很快就掌握了产生‘平移波’的方法,重现了他在运河中看到的特殊景象。经过多次实验,反复研究,罗素注意到孤立子的许多特殊性质:一是孤立子的速度与波的高度有关,二是孤立子能够保持其速度和形状长时间地传播。比如,罗素经常在他的实验水槽里产生两个孤立子,一个瘦高个,一个矮胖子。有趣的是,瘦高个总是比矮胖子跑得更快,每次都能追上矮胖子。更神奇的是:两波相遇后,并不会混合乱套而失去它们各自原来的形状和速度,相遇再分开之后,高而瘦的波越过矮胖子,继续快跑,将矮胖子远远地甩在后面。 罗素认为,既然孤立子能够保持其速度和形状长时间地传播,它们应该是流体力学的一种稳定解,罗素对此提出了很多大胆的猜想和预言,但他一人单枪匹马,精力毕竟有限,便希望得到科学界的关注和共同研究。1844年9月,也就是在第一次观察到水波孤子现象的十年之后,罗素在英国科学促进会第14次会议上以《论波动》为题,对他的发现和研究作了一次精彩的报告。报告内容虽然另人们觉得神奇精彩,但却未能得到罗素期盼的结果。因为正如大多数革命新思想出现时遭遇的命运一样,罗素的想法未得到当时科学界权威的认可,反被某些评论者说成是因走火入魔而产生的“反常和漫无边际的猜测”。 在罗素去世十年后,1892年,两位荷兰数学家从浅水波运动的KdV方程,果然得到了与罗素所描述现象类似的孤立子解(图24.1c)。KdV方程证实了罗素观察到的两个孤波碰撞时发生的情况。两个弧波相交后,并不互相混合和弥散,而是各自保持它们原来的速度、方向和形状,完整复现出来。这种行为类似于微观粒子发生碰撞时的情形,这也是为什么将此现象称为孤立‘子’的原因。 从物理学的观点来看,孤子是物质色散效应和非线性畸变合成的一种特殊产物。 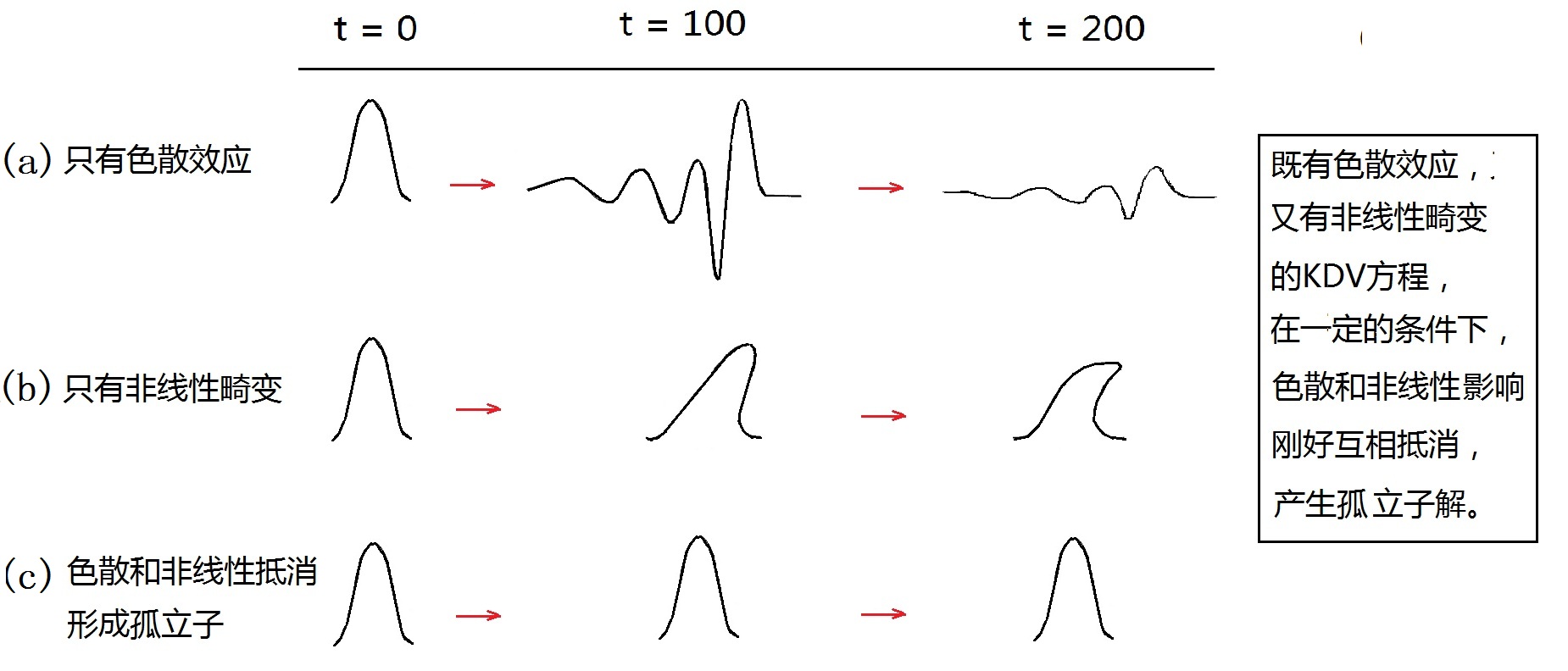
图(24.2):色散和非线性崎变抵消,形成孤立子 水波和光波等波动现象形成的波峰,都可以描述为由许多不同频率的正弦波组成。这些不同频率的波以不同的速度传播,这就是色散现象。在波动的线性理论里,各正弦波彼此无关,没有什么东西把这些不同频率的波捏合在一起,所以它们各自为政,即使一开始时候形成了一个巨大的波峰,这个波峰中的各个频率波也会因色散现象导致速度不同而使波峰很快地改变形状,破碎成许多小小的涟漪,形成浑沌而弥散开来。这是只有色散的情况,如图(24.2)中的上图所示。 从另一方面,流体分子间存在的非线性效应使得波峰的形状发生另一种类型的崎变,这种非线性崎变作用,如图(24.2)中的中图所示。 在KdV方程中,因为既考虑了色散现象,又包括了非线性效应的影响,所以,在一定的条件下,这两种作用互相抵消。色散效应要使得不同频率的子波互相分离,而非线性效应又将这些子波拉回来紧紧地拴在一起,这样一来,最后结果就使得原始的波峰既不弥散,也不崎变,而能够长时间地保持原状滚滚向前,这就形成了罗素看到的孤立波,也就是在图(24.2)中的下图所示的情形。 尽管数学家已经证明了KdV方程的确存在类似孤立子的解,人们对罗素发现的孤立子的重要性仍然认识不足。孤立子的命运一直到上世纪60年代才有了转机。20世纪50年代,美国的三位物理学家费米、帕斯塔和乌拉姆,利用当时美国用来设计氢弹的大型计算机,对由64个谐振子组成的非线性系统进行数值模拟,企图证实统计物理学中的“能量均分定理”。但他们的模拟结果却事与愿违,违背了能量均分定理。初始时刻这些谐振子的所有能量都集中在某一振子上,其它63个振子的初始能量为零。按照能量均分定理,系统最后应该过渡到能量均分于所有振动模式上的平衡态。但实验结果却发现,经过长时间的计算模拟演化后,能量出现了“复归”现象,大部分能量重新集中到初始具有能量的那个振子上。 费米等人当时只是考虑实验振子在频率域的情况,并且因为结果出乎意料地违背了物理界原来公认的“能量均分定理” ,所以,他们并未将此现象与罗素发现的平移波联系起来,因而也与孤子的发现失之交臂。但后来有人继续费米等人这项研究时,得到了孤立波解,并从而进一步激起了人们对孤立波研究的兴趣。其后,物理界对孤子现象的本质有了更清楚的认识,除了水波中的孤子之外,并先后发现了声孤子、电孤子和光孤子等等现象。小小的孤立子不再孤独,被人们誉为“数学物理之花”。 由于孤子具有的特殊性质,使它在物理的许多领域,如等离子物理学、高能电磁学、流体力学和非线性光学等领域中得到广泛的应用。此外,孤子在光纤通信、蛋白质和DNA作用机理,以及弦论中也有重要应用。 特别是在由光纤传输的通信技术中,光孤子理论大展宏图,因为光孤子在光纤中传播时,能够长时间地保持形态、幅度和速度不变,这个特性便于实现超长距离、超大容量的、稳定可靠的光通信。 1982年,在罗素逝世一百周年之际,人们在他策马追孤波的运河边树起了一座纪念碑,以纪念这位孤军奋战、但有生之年未能‘成功’的科学先驱。 参考资料: 【1】http://en.wikipedia.org/wiki/John_Scott_Russell 【2】Mark J. Ablowitz and Douglas E. Baldwin,Nonlinear shallow ocean-wave soliton interactions on flat beaches,Phys. Rev. E 86, 036305 (2012),Published September 6, 2012。 上一篇∶無序到有序 返回目录 下一篇∶生命遊戲 | 