戴榕菁 我知道在賈尼別科夫效應這個問題上,對於某些人來說,如果不聊聊數學,你就是讓他看一萬個視頻他心裡還是不踏實,畢竟這裡涉及到了角動量守恆這個被認為是物理學基石的議題。那麼咱們就來聊聊數學。下面是從維基上得到的對於賈尼別科夫效應的穩定性的數學分析的基本方程式【[1]】: 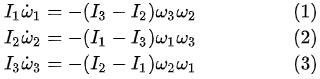
方程組(1,2,3)是著名的歐拉方程,其中I1,I2,I3是物體的主慣性矩且被假設為 I1 < I2 < I3 ω1,ω2,ω3是沿着三個主軸方向的角速度分量,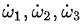 是三個主軸方向的角加速度分量。 是三個主軸方向的角加速度分量。 他們的分析的第一步就是將上面方程組的(1)式對時間求導並將(3)式中的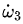 代入求導的結果從而得到: 代入求導的結果從而得到: 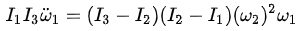 (4) (4)
因為I1 < I2 < I3,所以(I3 - I2)( I2 - I1) > 0 由(4)式他們得出結論說,只要一開始的時候ω1有一個非常小的值,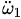 就有一個大於零的值,也就是說 就有一個大於零的值,也就是說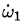 會越來越大。 會越來越大。 這裡要注意這樣兩點: 1)歐拉方程組(1,2,3)的前提條件非常明確:沒有外力。這使得我在前文“再聊聊賈尼別科夫效應”【[2]】中對於不存在外力的討論顯得多餘了。 2)從前面的(4)式可以看出,這並不存在一個奇異點的問題,因而按照(4)我們是可以算出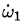 的不斷增大的值的。但是 的不斷增大的值的。但是 3)我們再來看下面兩個視頻: https://www.youtube.com/watch?v=Xrf1HzFJ8jc&t=27s https://www.youtube.com/watch?v=1x5UiwEEvpQ 從上面兩個視頻可以明顯看出的ω1方向在來回的翻轉中是不斷變化的,也就是說不可能是沿着一個方向不斷增大的。而(4)式中除了ω1之外都被假設是不變的,因此只要ω1的初始值大於零,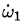 就總是大於零的。。。。由此可見,在太空站中的實際的賈尼別科夫效應運動與(1,2,3)方程組所描述的運動相去甚遠! 就總是大於零的。。。。由此可見,在太空站中的實際的賈尼別科夫效應運動與(1,2,3)方程組所描述的運動相去甚遠! 討論 對於滿足於所謂的穩定性分析結果的人看了上述分析之後一定會說:(4)式樣說明了物體沿着最小慣量軸的加速度會不斷增大,從而會使ω1大到能翻轉的程度就行了,不必繼續給出翻轉後的運動是什麼樣的了。 但問題是,如果你相信歐拉方程可以準確地描述太空站中的賈尼別科夫效應運動,你有什麼理由告訴我們物體的實際運動會不符合(4)式的描述? 其實,如果你說“太空站中的賈尼別科夫效應運動是在ω1可以不斷增大這點上滿足歐拉方程,但是當物體開始翻轉後的運動就不需要滿足歐拉方程”,你等於在說太空站中的賈尼別科夫效應運動打破了角動量守恆----這是因為歐拉方程等價於角動量守恆。。。。如果你沒有特殊的理由(諸如假設運動可以不滿足角動量守恆這樣的理由),你就不能說ω1大到一定程度之後就可以不滿足歐拉方程了。 現在想想,也難怪被西方譽為當代最偉大的數學家之一的陶哲軒會用內力來解釋太空站中的賈尼別科夫效應運動的總角動量的變化。。。。其實,本文所引用的據說是已經有將近兩百年歷史的分析其實質就是用內力來解釋----因為它的出發點就是假設沒有外力。 但是,我們知道牛頓定律的最基本的一個結論就是在沒有外力的前提下,物體的總角動量是不會變的。 歐拉方程是我在北航讀大學時的理論力學課上學習的(那時候賈尼別科夫還沒有發現他的效應呢),剛才為了寫這篇文章又重新複習了一遍它的推導,並沒有發現什麼問題。。。。當然,以大數學家歐拉的名頭來說,我們似乎也不應該懷疑它有什麼問題。 但另一方面,本博客之所以如此地要在太空站中的賈尼別科夫效應運動這個問題上冒觸犯角動量守恆之大不韙而固執地叫真,最主要的是因為實在無法從任何現有的視頻中看出在物體翻轉過程中的總角動量可以在任何意義上等價於最初的角動量。。。。 不論你如何強調只要最初有一點點沿最小慣量軸的角速度,歐拉方程就能讓它變得很大,哪怕你說破了天,只要你的前提假設是沒有外力矩,那麼在包括翻轉在內的整個運動過程中總角動量就不能變!!!因為只要它一變就打破角動量守恆! 但是,你們誰能看出下面這個視頻中的總角動量是守恆的:(???) https://www.youtube.com/watch?v=Xrf1HzFJ8jc&t=27s 其中最明顯的一點是在沿着中間慣量軸的轉動方向相同大小基本相同的前提下,沿着最小慣量軸的翻轉方向可以一會兒保持不變一會兒完全相反,根本沒有定數-----這根本不可能保持總角動量不變!!! 結束語 前面提到,現有的用歐拉方程來對賈尼別科夫效應運動進行的所謂的穩定性分析的前提都是沒有外力作用。在這樣的前提下他們居然可以完全不顧所有來自太空站的明顯不滿足總角動量守恆的現象而盲目滿足於“穩定性”這個大名詞帶給他們的安全感。 但另一方面,人們假定太空站里的賈尼別科夫效應運動沒有受到任何外力作用是一回事,而太空站裡面到底是否實際上有可以影響賈尼別科夫效應運動的外力又是另一回事。從這個意義上來說,我在前文“再聊聊賈尼別科夫效應”【2】關於太空站中是否可能有實際上會影響賈尼別科夫效應運動的作用力的討論就很有意義了。 這裡再針對太空站里是否會有影響賈尼別科夫效應運動的外力這個問題多說幾句。 如同在大氣層內的物體在空中的運動一樣,我們首先要考察的就是兩種力:重力和空氣作用力。
由於太空站內處於微重力環境,如我們從視頻上看到的,重力的影響可以直接忽略,這一點我在“再聊聊賈尼別科夫效應”也討論過了。至於空氣作用力,既然人能夠在裡面生存,那就一定會有空氣作用力。但是,了解空氣動力學的人都知道,空氣對於太空站內的物體的作用力屬於是阻力,而且在這種低雷諾數的範圍里可以引起局部振動的湍流都不會有,因而不具有可以讓物體做來回周期性翻轉的能力。所以空氣的影響也可以被忽略。那麼是否存在其它的諸如電磁力之類的隱形作用力呢?這一點就回到我在“再聊聊賈尼別科夫效應”一文中的論點,從視頻中的賈尼別科夫效應運動的周期性翻轉特性來看,我們也可以否定它們是由電磁力這樣的隱形作用力造成的可能。 所以,除非有什麼我們人類目前還不知的自然力在起作用,通過我最近幾篇文章的討論,我們可以相當確定地說:太空站里的賈尼別科夫效應運動打破了角動量守恆定律!!! 現在我們實際上面臨着這樣兩個層次上的問題: 1)為什麼會出現角動量明顯不守恆的現象? 2)為什麼Pointsot簡化了的歐拉方程會得出角動量不守恆的結果? 這是兩個不同層次的問題,彼此之間不一定有着必然的聯繫。比如說,假如從角動量守恆出發的歐拉方程的推導或Pointsot對歐拉方程的運用中存在問題,那麼上面就是兩個完全不同性質的問題。。。。但是,如果歐拉方程的推導沒有問題而且Pointsot對歐拉方程運用也沒有問題的話,那麼上面就是兩個彼此關聯的問題了。 相關鏈接: 再聊聊賈尼別科夫效應 難道被蘇聯封了40年的真正秘密是。。。?
-------------------------
[[1]] Wikipedia. Tennis racket theorem. Retrieved from: https://en.wikipedia.org/wiki/Tennis_racket_theorem. Last edited on 29 November 2024, at 06:27 (UTC). 【[2]】戴榕菁(2025)再聊聊賈尼別科夫效應 
| 