相信很多人都滚过雪球。要滚起一个雪球,从零开始的话,先用手捏一个小雪团,然后利用雪球表面对雪的亲和力逐渐滚大。在雪球小的时候,很难滚,增加一倍的体积要花费较长的时间,还要仔细,因为一不小心,雪球就滚散了,而当雪球滚到一定的体积时候,就容易多了,体积越来越大,每滚一次沾的雪就越来越多,雪球就容易滚多了,还不容易融化。 自然科学中有许多类似滚雪球的原理和现象。 学过化学的人都知道酸碱滴定,氧化还原滴定。在最初的反应烧瓶里,加入很多滴定剂,指示剂的颜色不变,但是在等当点附近,半滴滴定剂就能使指示剂的颜色变化(一般是从红色变到蓝色)。这是因为在等当点附近,溶液的pH值或者E值发生了一个突变/飞跃,这可以用实验图谱表示出来:
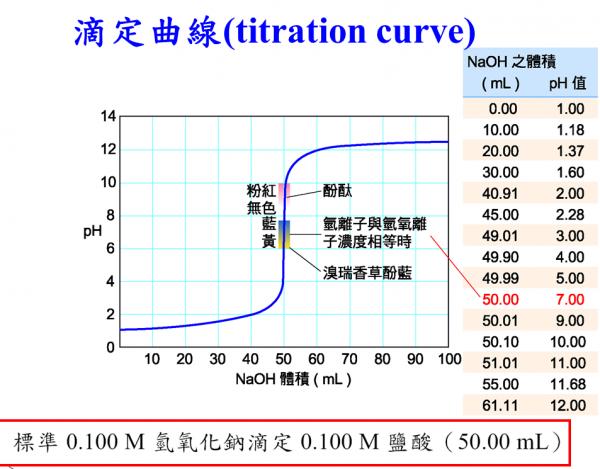
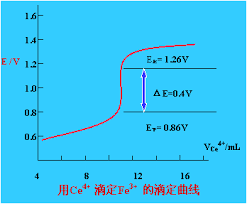
细菌培养也是这样的。在一个培养皿中加入一定的培养液,接种以后,一定的条件下,细菌的浓度开始随时间的变化很慢,要经过一段时间培养后,细菌才进入对数生长期,这时的细菌浓度会发生一个突变,陡然增加,这也可以用实验图谱表现出来:
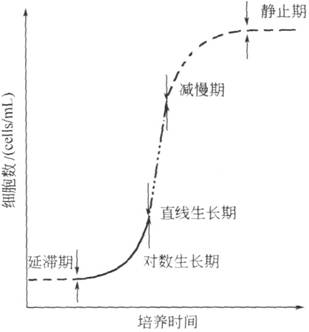
仔细分析起来,社会科学中的种种情形也是如此,也符合滚雪球情况。知识、财富和人气的积累,都是和滚雪球一样。从零开始积累的时候都很艰难,有人成功,将雪球滚大,有人失败,将雪球滚散。
诚然,社会科学似乎更复杂些,因为这里牵涉到更多的变量。人类社会中的任何成功都离不开天时地利人和。 其实,滚雪球现象,有个很学术的名字:叫马太效应。《新约马太福音》中有这样一个故事,一个国王远行前,交给3个仆人每人一锭银子,吩咐他们:“你们去做生意,等我回来时,再来见我。”国王回来 时,第一个仆人说:“主人,你交给我们的一锭银子,我已赚了10锭。”于是国王奖励他10座城邑。第二个仆人报告说:“主人,你给我的一锭银子,我已赚了 5锭。”于是国王例奖励了他5座城邑。第三个仆人报告说:“主人,你给我的一锭银子,我一直包在手巾里存著,我怕丢失,一直没有拿出来。”于是国王命令将 第三个仆人的一锭银子也赏给第一个仆人,并且说:“凡是少的,就连他所有的也要夺过来。凡是多的,还要给他,叫他多多益善。”这就是马太效应。 看看我们周 围,就可以发现许多马太效应的例子。朋友多的人会借助频繁的交往得到更多的朋友;缺少朋友的人会一直孤独下去。金钱方面更是如此,即使投资回报率相同,一 个比别人投资多10倍的人,收益也多10倍。 在同一起点,同一社会环境的条件下,对大对数不是含着金勺子银勺子出世的吃瓜大众来说,创业时期是非常艰难的。这就是大家说的第一桶金非常难挖。当经过不懈的努力,成功了,终于积攒到第一桶金的时候,后面再发展、再赚钱就容易多了。 绿岛个见:个人的经济发展如此,国家的经济发展也是如此。一切对社会对个人的评价和期望,用辩证哲学的滚雪球原理来分析,才会得到理性、客观和科学的判断和结论,从而不会对自己、对他人、对社会产生过高的期望,从而避免失望。
|
