多维空间真的存在吗？

特有理

2016-5-26

人的思维并不是孤立的。一个思维概念的建立往往具有更广泛的思维依托。在谈到时空问题的时候，相关问题必然会被涉及。谈时空的运动，怎能离得开对空间的思考？

近代的科学家们在捣鼓时变模型的同时，有些人也在论证多维空间的存在。其基本的理论依据，是由拓扑几何发展出来的多维空间模型。因该说，几何原理是一个非常基本，目前也已非常成熟的基础数学理论。在几何学基础上发展起来的拓扑学，随着解析几何以及计算机图形技术的发展，已经可以把设想中的数学模型用计算机形象地展示出来。但是尽管多维空间的数学图形描述很具有高科技的派头，其空间的概念似乎偏离了实际空间的基本性质。典型的，就是数学中的矢量空间（Vector Space）。这种数学空间的概念实际上是就是借用了现实空间的广阔和全方位的意义，同时也包含了向量的方向性质和空间分布性质。当有人形象地将其称之为n维空间时，有思路宽阔者便将这种数学空间真当成了现实中存在的物理空间。

应当说，拓扑学是一个挑战人类形象思维的学科；同时，神奇的图形中又强烈地展示出数学的美妙。电影《盗梦空间(Inception)》中就大量使用了拓扑学中一些经典的模型来表达主题的深奥和玄妙。那些不可思议的图形空间，就像有魔力一般吸引着人们探寻它们背后的自然奥秘。其中有代表性的如莫比乌斯环（Mobius Strip）【图1】和潘洛斯三角（Penrose Triangle）【图2】。

                 
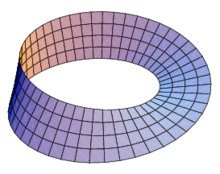
【图1】 莫比乌斯环                【图2】潘洛斯三角

有人说莫比乌斯环是一个二维空间，并以它只有一个面来解释，这只能说这些人没有真正理解二维空间的定义。二维空间只能出现数学的概念中，它的数学模型是F=f(x, y)，只能有两个变量。而莫比乌斯环必须要有三个变量才能生成，因而它也是现实的。

这里，有必要对所谓的零维空间、一维空间、和二维空间做一下说明。一般的陈述都说：零维空间是一个点，一维空间是一条线，二维空间是一个平面。这其实是一种形象的说法。在数学体系中，空间实际意味着变量的集合。零维空间意味着没变量，唯一的意义是它在高维空间中的参照位置。它既不是现实空间中的一个点，也没有大小、没有方向。同理，数学中一维、二维、三维空间虽然以形象的线、面、体来对应，但这些空间只具有几何性质而并不具有物理性质。也就是说，我们可以形象地描述它们的长度、面积、体积、形状；但是我们不能赋予线以粗细、面以薄厚、体以轻重的概念。特别在现实的物理世界，能量的传递是无法在三维以下的空间进行的。因此，虽然说线上有无数个点、面上有无数条线、体中有无数个面，这些都只是我们思维中形象的概念。

现在，我们探讨一下多维空间的代表，所谓四维空间中的“超级方块”，英文统称：Hypercube ，专称：Tesseract【图3】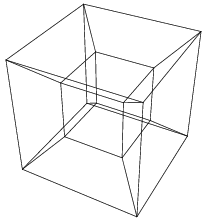

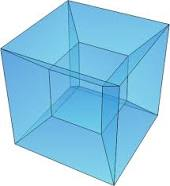
【图3】设想中超级方块在三维空间的投影模样

这是一个设想中的超级方块从四维空间投影到三维空间再到在二维平面的投影。它的生成概念是由点的延伸成为线，线段的平移生成平面，平面中的正方形沿垂直方向移动等边距就形成了立方体。把这个思路扩展，沿想象中四维轴线，把三维的方块移动一个边距的距离，其组成的空间就是四维中的超级立方体。【图4】

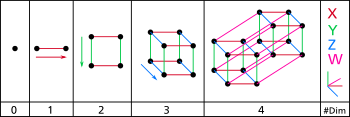
【图4】不同维度空间的转换

按照专家们思路，二维平面在一维空间的投影是一个线段，三维物体在二维空间的投影是一个面，那么四维空间在三维空间的投影就是一个体。如果只保留三维体的边棱，那么在二维投影中就能看到空间的三维物体的模样，如各种多边体的所有顶点和棱边。【图5】

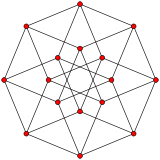
【图5】超级方块的正交投影

可以说三维图形在二维空间的投影通过顶点和边棱保留了三维的一些信息，因此还是能够在人的眼中形成立体感。这在人们的常识感中是一点没错的。比如图1、图2、图3，甚至图5也可以在想象中建立起立体的感觉。其实这应该归功于人大脑对图形的处理功能和视觉形象对应功能，这是对记忆中的物体进行对照的过程。这也说明人具有从简单信息探究实质的天性。不过，这种立体还原的感觉有时也会带人误入歧途，图2中的潘洛斯三角就是由阴影构造出的非现实立体描述。它在真实的三维空间中是不可能实现的。

所谓的投影，完全是现实空间中光线在物体表面留下的光影，这与数学中平面与三维图形相切并不完全是一个性质。比如一个复杂形状的三维物体，它的投影与在某一位置做出的数学切面有可能相差甚远。即使实际投影与数学切面完全一致，投影也必须有物理界面。之所以提到这个问题，是因为所谓四维物体向三维投影的说法并没有物理依据。在数学空间中，投影实际是将变量的变化进行平面限定，最简单的，就是设某一维的变量为零。这就引出这样一个问题：四维空间的物体如何投影在三维空间？根据超级方块“专家”们的观点，四维的物体在三维空间的投影应该是三维的。这从数理逻辑上没错，但这应该是一个真实的三维影像才对。因为三维到二维的投影是一个真正的二维影像，二维到一维也是一个真正的一维影像。问题是，四维到三维的投影如何实现？

现在网络上可以找到不少描述和解释超级方块的视频，其中都讲到了投影，也都提到了将三维体旋转的概念。比如多棱体通过旋转或滚动，在二维平面上展示出各个顶点和棱边的相对变化，并以此在二维空间获取三维物体的信息。这本身就是一个认知悖论。因为声称三维以上空间存在的人，为了解释人为何无法感知到那些空间，都会确定一个前提：即低维度的生物无法感知到高维度的空间，例如二维的生物，如果有的话，就感知不到立体的三维空间，所以人也感知不到三维以上的空间。那么三维物体旋转或滚动的投影信息，二维生物能否感知到？如果二维生物能感知到二维的投影图形以及它们的变化，这在逻辑里也是必须的，那么二维生物为什么不能像人一样通过数学公式，推算出三维物体的形状？如果人能利用数学模型解析四维甚至更高维度的形体，二维空间的生物也应该能做到才符合逻辑。

而且，一维、二维有生物的假设本身就是一个错误的前提。因为那根本就不是真正的物理空间，也没有物理空间可以存在。用一个虚拟的错误假设与现实的逻辑进行对接，从而推论出人无法感知高维空间，并以此躲避现实的验证，实际上就是一种学术上的欺骗。许多打着科学名义行骗的人，都是利用人们以开放的态度接受分析假设的心理，把错误假设中的逻辑与现实嫁接，再将其按现实逻辑进行现实推论，不管结论是否蒙对，其方法肯定错误的。

如果我们跳出正方形或多边体的局限，思考一下具有普遍意义的空间性质，就会发现：【一维空间是点沿一个方向膨胀的结果；二维空间是点沿着与一条穿过该点的参考线的垂直方向任意膨胀的结果；而三维空间则是点沿任意方向膨胀的结果】。那么四维空间在点的基础上该如何膨胀？如果我们把投影看作是一个光线扫描的过程，则三维投影应该是光线在任意角度方向扫描的结果。由此可以看出，人们定义的笛卡尔三维空间的实质，就是数学中广义的n维空间。这里的逻辑关系是：如果三维空间是一个点向任意方向扩张的结果，如果三维投影是由任意角度光线扫描所完成的，那么所谓的3+n维空间的物理模型就是与三维空间等效的。因为在三维基础上的“任意的任意”，从逻辑上讲是没意义的。因而在具有任意方向的三维空间上再加上一个假想的任意方向的第四维就只能是虚拟的“意念维”。

三维以上的空间，以及四维的“超级方块”，其实是一种数学的演绎甚至是数学家们游戏。其它领域的人没有必要太纠结在所谓的“多维空间”，或是神秘兮兮的高维“超方”。电影《盗梦空间》中有这样一个情节：女设计师将路边的镜子拉到相对位置，镜子里便出现了景象的无限重复和延伸，我想这就是导演要表达的n层梦境，实际上就是所谓的n维空间。同样，当我们把三维方块模型放在镜子前面并且不断转动，方块和镜中影像的组合变化，这就是拓扑学家们所说的，方块沿第四维空间轴移动的形象概念。