三十多年后，也票一把“哥德巴” “一九七八年发表在《人民文学》第一期的轰动一时的报告文学《哥德巴赫猜想》，至今仍被文学界和读者常常提及和谈论，三十年过去了，这篇报告文学的作者徐迟和主人公陈景润皆已去世，他们曾经感动和激励着一代人为“科学的春天”奋斗，为改革开放的伟大事业奋斗。” --http://www.rmwxzz.com/rmwx/tx/200803/18384.html 当时还在窑头搬砖的我，也不例外地对于科学的春天（特别是稍后教育的春天）深感振奋，但是对于哥德巴赫猜想的具体内容和陈景润的研究，对于1+2，无可奈何地一头雾水；三十多年后，仍然雾水一头。 某日心血来潮，想用外行的角度和语言，把这个问题搞搞清楚：专业语言没希望了，试着用老百姓的话来理解一下？我断章取义地相中了这段话： “欧拉在回信中也提出另一等价版本，即任一大于2的偶数都可写成两个质数之和。今日常见的猜想陈述为欧拉的版本。”（百度百科） 徐迟的报告文学则说：“一七四二年，哥德巴赫发现，每一个大偶数都可以写成两个素数的和。他对许多偶数进行了检验，都说明这是确实的。但是这需要给予证明。因为尚未经过证明，只能称之为猜想。他自己却不能够证明它，就写信请教那赫赫有名的大数学家欧拉，请他来帮忙作出证明。一直到死，欧拉也不能证明它。从此这成了一道难题，吸引了成千上万数学家的注意。两百多年来，多少数学家企图给这个猜想作出证明，都没有成功。” 据说，“每一个大偶数都可以写成两个素数的和”就是陈景润至死也没搞掂的1+1。这句话，比较接近生活语言，我就盯上它了—想把一些概念搞搞清楚，扫扫盲。 我比较喜欢问“为什么”，这里就难免要问：一个隔三岔五的质数表，选其中的（特定）两个，就能合成任何一个大偶数，凭什么？这里的话音儿，显然不是想“证明”什么，而是刨个根儿，怎么会子事嘛？ 一番阅读加体会后，我快快写了个（VB的）程序，试着把自己的理解写进去（见下）  屏幕的右上角，是用户（我）要输入的一个偶数。我先选择了18 （简单点，便于理解；数目搞大了，容易头疼。）
然后按“Draw Matrix”（画出方阵）的键—先是在两个list-boxes 加入（同样）的两行质数系列， 都小于自选的18（大于18，对当下无用。） 然后，从3开始，把能够组合出来的“任选二”都组一遍，把这两个质数之和，写在方阵里。（不重复的组合—如图中蓝线所示--其实构成的是个三角形，所以把多余的【镜面】部分用红线勾掉.） 程序然后计算出下面的（统计）数字：由3-17这6个（小于18的）质数，任选二个，共组合出了14个不同的偶数：6、8、10、12、14、16、18、20、22、24、26、28、30、34. （其中缺了32，倒不是说人家哥德巴赫“猜”错了，只不过我选的上限是个18，我只关心6至18这中间有木有缺失的偶数。只要程序逻辑无误，6至18这7个连贯的偶数（6、8、10、12、14、16、18）就都在方阵中出现了。预计的偶数个数是7，任意选二组合出来的distinct偶数也是7—这就是我期待的信息：任选一个偶数N，由此确定出一个大于等于3并小于N的质数系列，从中任意选二组合出来的distinct偶数，必能涵盖6至N（即选定的上限值）这中间的全部偶数（包含6与N）。 我注意到所期待的偶数有重复的现象—如10和16，因为能构成10和16的，不止一组质数。我心里莫名其妙地轻松了一下：啊，如果任何一个偶数，只能由独特的一组（二个）质数相加而成，那就过于完美了，现在明显不是如此。 显然，一旦一个偶数上限提出，剩下的就是完全被限定、注定了的（包括哪几个偶数会在方阵中重复出现，重复几次，都是华山一条道，毫无通融之余地—除非你改变了质数的定义。） 对于我这样的外行来说，那6到18中的诸个偶数，为什么必然是两个（小于18的）的质数之和，应该说是有了一个逻辑性的眉目了。您也许会说，这么初级的东西，还拿出来讲？对不起，对我来说，已经相当费力了。证明的事儿，还是留给别人吧。我能做的，就是把越来越大的偶数上限输进去，看着那个（已经没有疑问的）结果出来。对了，这个上限在于我这个潦草的程序还是有局限性的—太大了不行，会有Overflow的危险的。（下面是一个稍稍提高了的上限：80）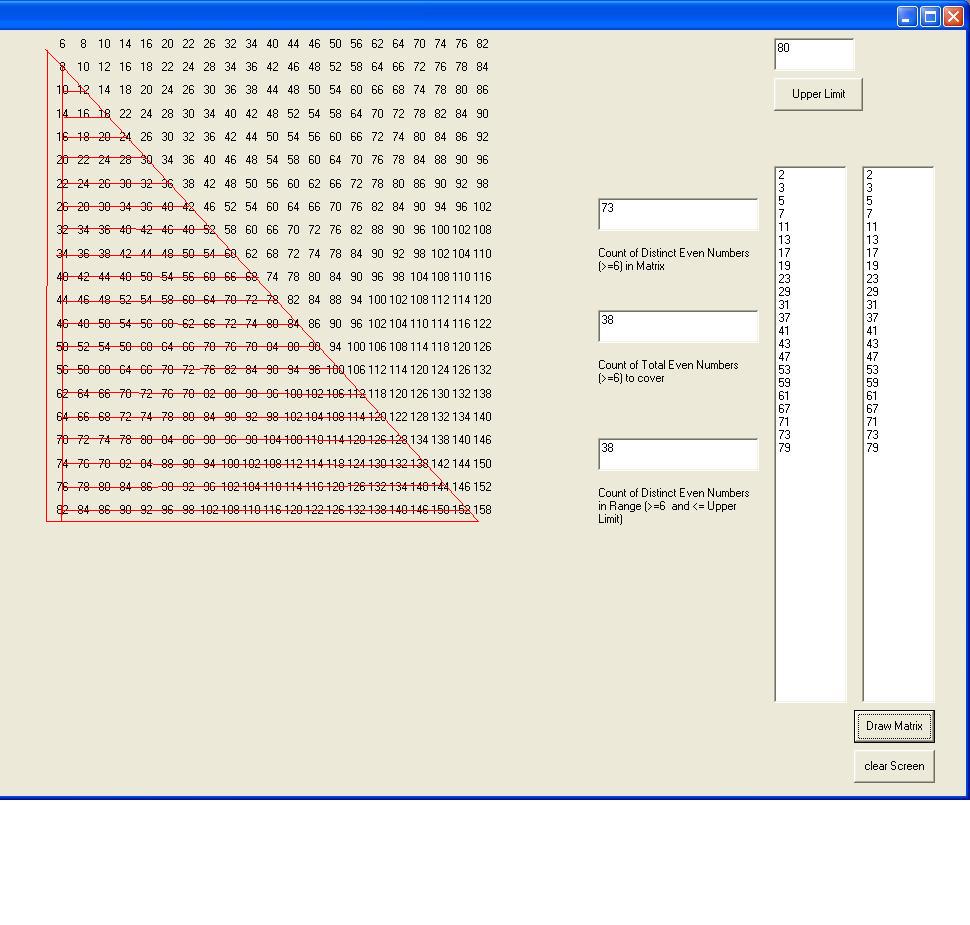 
|
