戴榕菁
1. 关于标题的解释 原本想用“揭密薛定谔方程的推导”为本文的标题,意思是想要揭示薛定谔在他的诺贝尔获奖文章中所给出的对他的那个后来成为量子力学之基础的方程的推导之真相。后来转念一想,既然人家自己在获奖文章中没有明说,纵然我这里将要演示的确实是薛定谔当初的思路,我也不能用“揭密”这个词,因为要说揭一个与人家本人的陈述相悖的密多少是带有对当事人不恭敬的味道,更何况这里的当事人早已不仅仅是薛定谔本人那么简单了,至少诺贝尔委员会也应该算是当事人吧,说薛定谔方程是推导不出来的但却真实反映自然的费曼也一定算是当事人吧,再往大了说,1926年后的整个20世纪物理学界都应该算是当事人吧。所以,我决定用“探秘”而不是“揭密”。 说到这里,且不说我所揭的或探的正题是什么,有读者可能已经对上面提到的“揭密”一词感到别扭了,因为按照中文词典上介绍的一般用法,人们会说“揭秘”而不是“揭密”。不过我上面之所以提到“揭密”而不是“揭秘”的原因也正是我决定用“探秘”而不是“揭密”的原因------虽然“秘”与“密”两个字合在一起组成的“秘密”指的是不为人知的事,但“秘”指的是自然的,而“密”指的人们刻意为之的。我原本想用“揭密”正是因为我隐隐地感觉这背后似乎有作者刻意为之的影子。。。。这种刻意为之的影子才是近一百年后我们有必要讨论它的真正意义;但也正是“密”字所带有的刻意为之的意思让我感到“揭密”一词过于带有诛心的味道了。人家费曼说的多圆滑呀:薛定谔方程是不可能按照任何一个已知的知识推导出来的,但它是正确的。尽管我最多只能在近似的意义上接受费曼所下的“正确”的论断而无法将他的论断照单全收,我也还是觉得应该参考一下这位以说出“shut up and calculate”这句明显反哲学的武断的名言著称的费曼在评论薛定谔时表现出来的语言技巧呀。 但是,如果让我将“揭密”改为“揭秘”我又实在改不下去,因为那就不是技巧的问题了而是要我承认这背后一定不存在当事者刻意而为的问题了。就算我没有资格断定当事者一定是刻意而为,我也同样没有资格断定他一定就没有刻意而为。所以最后选定“探秘”这个词。既然是“探”,那么到底是自然的还是当事人刻意而为的就不重要了。尽管在下面的讨论中为了方便我仍要假设我知道薛定谔的某些做法的目的,读者尽可以把我的讨论看成是在说李定谔或杨定谔而不是薛定谔。 2. 问题的背景 十多天前我在“戏剧性的薛定谔”【[1]】一文中对薛定谔在他获得诺贝尔奖的那篇文章【[2]】中所介绍的他的举世著名的方程之推导过程进行了讨论。在讨论的过程中有一个细节特别引起了我的注意,那就是薛文中的第(13)式: 
这(13)式明显就是著名的德布罗意获得诺贝尔奖的波长公式。但问题是:正如薛定谔在他的文章明确地宣称的他在推导过程没有用到相对论,而如我在2023年【[3],[4]】已经一步步地详细指出的,假如德布罗意当初没有用到相对论,那么他的波长公式就不会是如上面所示的薛文的(13)式的结果,而会是: λ = 2(v2/c2) h/p = 2(v2/c2) h/mv (*) 也就是说,假如薛定谔的推导是在逻辑上严格的而且没有用到相对论,他根本就不可能得出上面的(13)式,而应该得出上面的(*)式。 不仅如此,我们还可以注意到薛文的(11)式是: 
这(11)式正是著名的爱因斯坦-普朗克光能公式,是爱因斯坦获得诺贝尔奖的公式。 薛文声称该文的(11)和(13)都是从下式按照正常的逻辑推导自然地得出的: 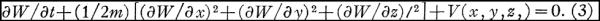
但是,如我上面提到的,他居然能在没有用到相对论的前提上得出只有用到相对论才能得到的结果,这让我感到他的那个所谓的推导不是从那个连单个质点在引力场中的自由落体运动都无法满足的(3)式(参见【1】)出发的,他应该是从在他的那个年代已经非常著名的(11)式和(13)式出发倒着推出那个没有人能正常得出的(3),然后再从(3)式出发貌似正常推导地叙述到(13)式,然后再接着进行他后面的讨论的。 3. 倒推薛文的出发方程(3) 那么我们来看看是否可以通过一般的科研的手段来从(13)及(11)推出(3)呢。 首先,假如我们有一个波函数如薛文的(9)式表示的为: 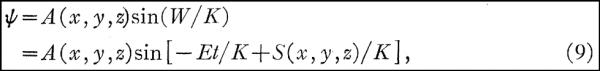 那么我们从(9)式可以直观地看出薛文中表达频率ν的(10)式以及薛文中极为关键的(4)式: 那么我们从(9)式可以直观地看出薛文中表达频率ν的(10)式以及薛文中极为关键的(4)式:

和 
在(10)中,我们只要令K = h/2π,就可以如薛定谔在文中宣称的那样很自然地得到上面的(11)式了,然后再用(11)式和下面将要得出的(6)就可以得到(13)式了。 所以,从(11)式和(13)式出发,只要对正弦函数的特点以及课本上对于求解哈密尔顿偏微分方程的标准形式有所了解,就可以想到去尝试用(9)式作为Peter Debye教授在薛定谔所做的德布罗意波的讲座上要求薛定谔得出的波动方程【[5]】的解。 但另一方面,从粒子动能的基本表达式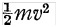 出发,并假设E为总能量,V为势能,m为质量,我们可以得到薛文中的(8)式: 出发,并假设E为总能量,V为势能,m为质量,我们可以得到薛文中的(8)式: 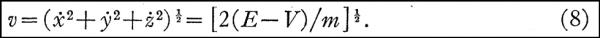
在接下来的一步中我们可以毫无逻辑地假设: 

同样我们也可以写出关于py和pz的类似的表达式。 上面的(2)与(7)式都是薛文中的等式,但显然我们由(2)能够合逻辑地得出的应该是 ∂W/∂x = mẋ - ∂V/∂x + 常数, 而不是上面的(7)。但薛定谔就愣是既给出了(2)式又写出了(7)式,并声称这是众所周知的,而诺贝尔奖委员会看来也okay,所以我才在上面说“在接下来的一步中我们可以毫无逻辑地假设”。 另外,如我在【1】中指出的,薛文中给出的上面(4)式原本是教科书上求解哈密尔顿偏微分方程的标准解形式,只不过作为一般的数学方程,E并没有特殊的意义。薛定谔将(4)作为他的那个谁也推不出来的(3)式的解时有这样两个基本的问题: 1) 薛定谔将E称为总能量,是一个常数,S是x, y, z的函数。但问题是:如果E是总能量,那么我们应该有E = T + V,从(4)我们就应该有:∂W/∂t = ˗ (T + V )。但是,根据(2)我们却有∂W/∂t = T - V。 2)尽管(4)是哈密尔顿偏微分方程的标准解形式而且(3)的解也确实可以表达成(4)的形式,但这丝毫不能说明(3)就是标准的哈密尔顿偏微分方程,更不能说明(3)可以用来求解诸如单个质点在重力场中的自由落体运动的问题。 但不管怎么说,用(4)式和(9)式我们可以得出(11)和(13);相应地,上面由(11)和(13)反向猜出(4)式和(9)式也属于包括物理学在内的科学研究中常有的试解的方法,没什么大毛病。 在承认(4)式中的E就是总能量的前提下,由(4)和(7)我们可以推导出那个被薛定谔称作是哈密尔顿偏微分方程但实际并不是哈密尔顿偏微分方程而且没人能给出其真正推导的(3)式来。 接下来,因为在任意时刻t我们都有 |grad W|2 = (∂W/∂x)2 + (∂W/∂y)2 + (∂W/∂z)2,所以(3)可以被改写为: ∂W/∂t + |grad W|2 /2m + V(x,y,z) = 0, 而由(4)我们可以得到: ∂W/∂t = -E 将上面两个式子结合一下便得到薛文中的(5)式: 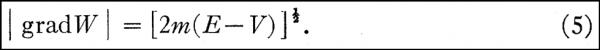
(5)在薛文中是非常关键的一个式子。薛定谔正是用(5)来将粒子动力学与波动联系在一起的。接下来的一步是重复薛定谔的(正确)叙述: 对于任意一个给定的时刻t,空间中的任意一个函数W可以表达为一组其值为W的值(例如W0)的曲面。但另一方面,我们可以从W0开始任意一组其值为W的空间曲面来得到(5)式的解。这是因为我们只要假设W0的某一边的W值为正,在W0上的这一边的每一点的法线上取长度为: 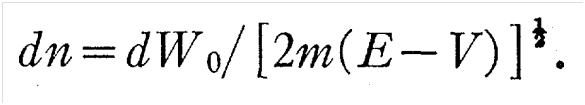
这样得到的所有的点的值显然是W0+dW0。依次下去便可得到在给定的t瞬间的所要的整个曲面系统。 由(4)可以看出,当时间改变时,上述曲面系统是不变,只是W的值沿着曲面的法向以下面的速度传播: 
这里薛定谔应该是用u = dn/dt 得出(6)的,只不过他把负号略去了,因为u只是相速度。 在得到薛文中的方程(6)之后,我们可以按照薛定谔的思路来考察普通的波动方程: 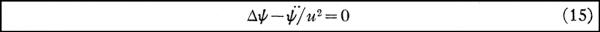
运用求解偏微分方程的最常用的变量分离法可以得到对时间变量的常微分方程(仍延用上面的ψ符号): 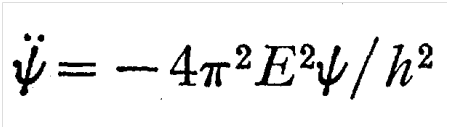
将上式与(6)代入(15)得到对空间的偏微分方程(仍延用同样的ψ符号): 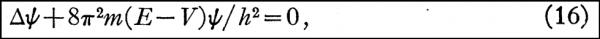
这就是薛定谔获得诺贝尔奖的著名方程,也是作为量子力学的基础的薛定谔方程的各种版本的最基本的版本。 4. 讨论 1)尽管上面的推导过程既不是大家所熟悉的老师上课演示的推导方式也不是任何一门理科考试中所允许的推导过程,我上面演示的各种猜解或试解却是科学研究尤其是物理学研究中非常常见的正常的手段。。。。只不过其中混杂了一些正常研究中按理说不被允许的步骤,比如薛定谔用“众所周知”这么一句话就给出那个(7)式的做法就不但不众所周知而且存在逻辑问题。 我上面的反推的目的是要向读者演示,假如站在当初薛定谔的位置上,我们如何可以根据当时已经获得诺贝尔奖的(11)和已经很著名的(13)式来完成Peter Debye教授给薛定谔提出的推导能够满足(11)式和(13)式的波动方程的任务。
我知道很多读者可能一上来会觉得上面的讨论有些吃力,但对于感兴趣并熟悉自然科学领域的研究的读者来说,我相信只要稍微花些力气还是能够从上面的讨论中看出这样的脉络:虽然在薛定谔之后没有人能够按照薛定谔的文章【2】中给出的思路推导出他文章中的(3)式来,我们却可以从我上面的讨论中比较清晰地看出薛定谔当初很有可能是从爱因斯坦已经获得诺贝尔奖的(11)式与德布罗意的已经成名的(13)式反向凑出(3)式来,然后再声称是从(3)式出发得出后面的结果的。。。。为了维护大咖薛定谔的名声,大家不妨把我这里所说的当作是在讲李定谔或杨定谔。 2)实际上,从我在文章【1】的讨论中我们已经可以看出,薛文中的(2)式的存在不但是多余的,而且还会直接导致逻辑矛盾。即便是将(2)式中的T – V 换成 T + V,仍然会导致个种矛盾。 不过,经过我在【1】和本文中的讨论之后,我们可以看出薛定谔之所以需要(2)完全是为了使他的推导有一个乍看起来的合法性。他的(3)根本就不是他所声称的哈密尔顿偏微分方程,但他又不但需要(3)而且还需要将(3)称作哈密尔顿偏微分方程,因为只有这样他才能假借哈密尔顿偏微分方程在经典动力学中的名声,让读者们以为他的(3)就是能用来求解动力学问题的方程。但另一方面,他又不能将(3)改写成真正的哈密尔顿偏微分方程的形式,因为那样一来他就无法用(3)和(4)来得出对他来说至关重要的(5)式了。。。。为了维护大咖薛定谔的名声,大家不妨把我这里所说的当作是在讲李定谔或杨定谔。
5. 结束语 如我在本文开头所说的,本文标题之所以叫做“探秘薛定谔方程的推导”而不是“揭密薛定谔方程的推导”是因为不想将本文的推测就认定为薛定谔当初得出他那个著名方程的实际过程。不过,既然没有人能够按照他的那篇获得诺贝尔奖的文章来合乎逻辑地重新推导出他的那个方程,而且他的文章中也确实存在一些明显的逻辑错误,我们可以合理地想象一下假如是李定谔或杨定谔站在薛定谔当时的位置要想从爱因斯坦和德布罗意已经得奖的两个公式来得出一个所谓的微观粒子的波动方程的话,他们可能会怎么做。。。。本文所做的就是这样一种工作。 如前所述,本文的起因并不是薛定谔文章中的明显的逻辑错误,也不是我们从视频中看到的那位曾说:“假如你在冰上摔疼了屁股,不要问我为什么。在物理学上不要没完没了地问为什么”的著名的诺贝奖得主费曼所说的“没有人可以从已知的任何内容得出薛定谔方程”这句话。。。。本文的起因是看到声称没有用到相对论的薛定谔居然在他们的文章中“推导”出了只有用了相对论才能得到的德布罗意波长公式! 最后顺便对我在2023年写的“德布罗意波之错和薛定谔之幸运”【3】一文及相应的英文版文献【4】稍作评论。在那两篇文章中我都提到了薛定谔方程因为拒绝使用相对论而不受相对论错误的影响。这一点现在看来是不对的。尽管薛定谔没有直接使用相对论,但因为他的方程是从德布罗意的波长公式出发凑出来的从而间接地受到相对论影响。 跟踪本博客从而了解自2022年初以来本博客揭示20世纪物理学弊病之进程的读者都见证了过去两年多的时间里本博客是如何在没有任何一个人的帮助下在上帝的带领下克服重重拦阻走过来的。本人并非物理专业人士,而面对的则不但是被整个物理学界奉为标准理论而且目前仍被整个物理学界加上庞大的科普队伍拼命维系的20世纪物理学。因此,大家应该预期会看到诸如我在2024年说的与2023年说的不同的现象。其实,这是我孤军奋战所出现的非常正常的现象。比起全世界数以千万计的专业物理大军在经历了一百多年的实践后仍死抱着20世纪物理学中的错误不放,我这里表现出的2024年纠正2023年的错误应该说是一件大好事。一切荣耀归于上帝。
【[1]】 戴榕菁 (2024)戏剧性的薛定谔 [[2]] Schrödinger, E. (1926). “An Undulatory Theory of the Mechanics of Atoms and Molecules”, The Physical Review, Vol. 28, No. 6, December, 1926. Retrieved from: https://web.archive.org/web/20081217040121/http://home.tiscali.nl/physis/HistoricPaper/Schroedinger/Schroedinger1926c.pdf 【[3]】戴榕菁 (2023) 德布罗意波之错和薛定谔之幸运 [[4]] Dai, R. (2023). Correction to de Broglie Wavelength. Retrieved from: https://www.academia.edu/111922499/Correction_to_de_Broglie_Wavelength [[5]] Up and Atom. (2019-12-12). [YouTube] What is The Quantum Wave Function, Exactly? [video] url: https://www.youtube.com/watch?v=EmNQuK-E0kI&t=9m22s
| 