2022-7-28

陪小不点儿做1997年的全美八年级数学竞赛AMC8(American Mathematics Competitions to students in grades 8 and below all over the United States)第十题，当时还不叫AMC8，叫美国初高数学考试（American Junior High School Mathematics Examination or AJHSME)。两年（1999）后才改用现名：

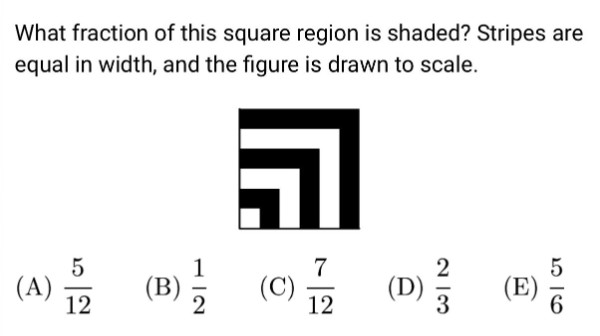
答桉自然不难，也有多种解法，最直接也最笨的方法，就是数有多少个四方块：

比较科学的办法，是把图形分解为六个边长分别为、1、2、3、4、5、6的矩形，叁条“7”形阴影的面积，分别用叁组矩形的面积差来计算：（36-25）+ (16-9) + (4-1) = 11 + 7 + 3 = 21。然后除以最大的矩形面积：21/36 = 7/12。做到这，小不点马上就说，这一道题似曾相识，和2007年AMC8的第25题异曲同工：

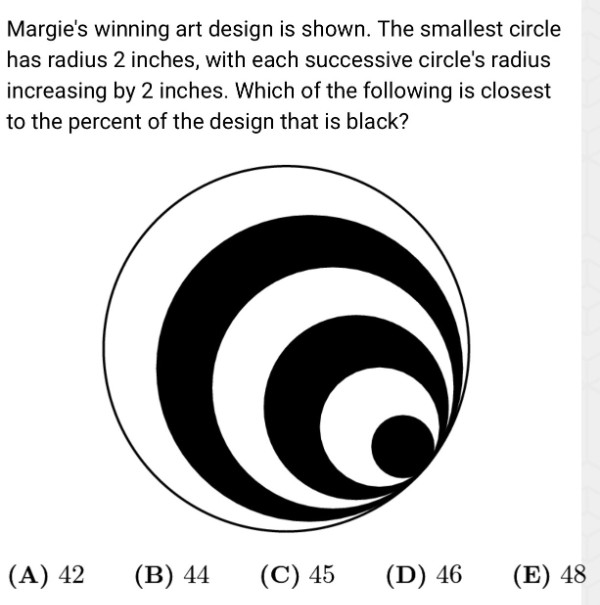
这道题的解法，就是和上面同样的思路：

当初小不点儿解这一道题的时候，写了足足的一大篇纸，还说特有成就感。