Music,  is an universal language of mankind

                     – Henry Wadsworth Longfellow, an American poet

    要知道乐器为什么能发出美妙的音乐，首先要知道声音是怎么来的。声音是自然界物体之间的碰撞冲击，导致空气压缩震荡，产生震荡波。震荡波有长有短，于是，人类的耳朵能感应到的就是不同的声音。自然界最美妙的声音无过于人类的歌声，世界上任何一种乐器，都无法超越人类的歌声，但是可以想方设法模仿，于是，各种乐器应运而生。

    首先，我们知道一个物理现象：拨动一根长丝竹，产生震荡发声。如果把长丝竹一切为二，再拨动那根短了一半的丝竹，震荡的频率提高了，声音相对也提高了（通俗地说，频率越高，声音越高，女高音的频率要比男低音的频率要高许多)。这就是说，音乐声和震荡频率是紧密联系在一起的。

    中国古代就有了如何定音律的方法，司马迁在《史记》中写道：“九九八十，一以为宫。三分去一，五十四为徴。三分益一，七十二为商。三分去一，四十八为羽。三分益一，六十四为角”。

    这是什么意思呢？意思是取一根用来定音的竹杆，长度为81单位，定为“宫音”。然后将81乘2/3，得到54单位，定为“徴音”。将54乘4/3，得到72 单位，定为“商音”。将72乘2/3，得到48单位，定为“羽音”。将48乘4/3，得到64单位，定为“角音”。这个方法叫做“三分损益”，产生了中国古代的五位定音：宫，商，角，徴，羽。也就是我们熟悉的简谱中的 1(do)，2(le)，3(mi)，5(so)，6(la)。 写成数学表达式：

    宫  81

    徴（损）81x2/3 = 54

    商（益）54x4/3 = 72

    羽（损 ) 72x2/3 = 48

    角（益）48x4/3 = 64 

    注意，这五音律的长度都是整数，都能被3除尽。这说明古代科学技术的限制范围，一根竹竿，也只能做到这些了。 

    中国明代音律学家朱载堉在1584年提出十二平均律。将一个音程的8度间，刻划成12个平均音阶。固定为首的那个作为基音，接下来的音阶，以 1.059463094公倍数，成等比级数，也就是说，前面一个音符乘上 1.059463094，就成了后面一个音符了。 

    后人推出2^1/12  （2开12次 方根）约等于1.059463094，这是个保留了9位小数点的无理数 。一个8度音程，通俗地讲，1(do)2(le)3(mi)4(fa)5(so)6(la)7(xi)8(do) ，被划分成12个单位，每单位为“半音符”，所以有了12个“半音符”。在算术上，这个8度音程开12次方根，求其平均，是符合逻辑的。朱载堉的思想是这样的：把事情倒过来算，知道了一个头，也知道了一个尾巴，中间等比级数的“倍数”就要硬算了。但是，16世纪还没有计算机，一个整数2要开12次方根，这可是件非同小可的事，不知道朱载堉花了多少天，用了多少草稿纸，又是如何折腾出这个数的，猜想和祖冲之计算圆周率有得一拼。这要专门研究数学历史的人，从历史古书中找到答案。中国的数学，严格讲是算术，是算出来的，没有体系。不像希腊人的欧几里德平面几何，一套理论体系很完整。

    欧洲的16-17 世纪，音乐处在巴洛克（Baroque) 时期，音乐的服务对象是教堂和宫殿。当时已有了一套完整的12平均律的乐器制作方法。 

    这是从Google那里copy 过来的部分数据来说明问题:

   Note     Frequency(Hz)     Wavelength(cm)

                  C₀                          16.35                            2109.89

                  C₀^# /B₀ ^b             17.32                            1991.47

                  D₀                          18.35                            1879.69

                   .                         .                                   .

                   .                         .                                   .

                 G₄                       392.00                           88.01

                G₄^# /A₄ ^b              415.30                          83.07

                A₄                         440                               78.41

                A₄^# /B₄ ^b              466.16                          74.01

                B₄                         493.88                          69.85

                  .                         .                                   .

                  .                         .                                   .

    先取A₄ ＝ 440 Hz，Wavelength = 78.41, （wavelength 相等于中国古代的竹竿长度）。为什么要取440 Hz，这是个conventional choice, 不是vital的（如果取 420Hz，产生的声音偏低，也可以取460Hz，得到的声音偏高，这由个人喜好，有人喜欢沉闷的声音，有人喜欢高亮的声音）.  我猜想, 440 Hz是个正数，便于计算。以A₄  Note为基音，定下了钢琴上所有的Note。 

    从这张图表中，观察到一个有趣的现象，值得注意：频律乘上波长是个常数（四舍五入），也就是声音在空气中每秒传播的距离，约等于34500cm。不信我们验证几个：

    对于 Note C₀  ： 16.35 x 2109.89 = 34497 cm／second

    对于 Note D₀  ： 18.35 x 1879.69 = 34492 cm／second

    对于 Note A₄  ： 440.00 x 78.41  =  34500 cm／second

    再来计算一下音阶，它们全是按等比级数，均匀分布的：公比正是上面提到的 2的12次方根， 约等于 1.059463094，不信我们试试：

    取A₄ 为基准音，它的频率取440.00Hz：

    下面一个Note是 A₄^＃/B₄^b  （在钢琴键上，是往高音走）

    它的频率是 440.00Hz x 1.059463094 = 466.16Hz,  再下面一个Note是 B₄  

    它的频率是 466.16Hz x 1.059463094 = 493.88Hz，等等。

    反过来:

    A₄  上面一个Note是 G₄^＃/A₄^b  （在钢琴键上，是往低音走）

    它的频率是 440.00Hz ／1.059463094 = 415.30Hz。 再上面一个Note是 G₄  

    它的频率是 415.30Hz／ 1.059463094 = 391.99Hz，等等。       

    依次类推， 求高音的，乘公倍数 1.059463094，求低音的，除公陪数1.059463094，用数学中recursive 的方法，我们可以得到钢琴上的整个音阶，乐器就是这么制作的。    

    欧洲的十七世纪，在音乐理论领域里，代表人物是巴赫 （Johan Sebastian Bach , 1685-1750)。巴赫是德国最伟大的古典音乐作曲家之一，他的Well Tempered Clavier 是钢琴专业学生的必修课。WTC 分上下两册，每册有24 首曲子，这是12 平均律在音乐上的体现：12 个大调和它相对应的Prelude 和Fugue，12 个小调和它相对应的 Prelude 和Fugue，总共48 首曲子。

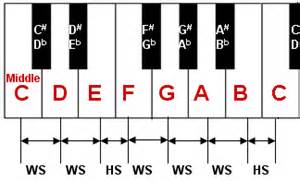
P1 - 这是钢琴键的中间部分，从C 到 C （CDEFGABC），一个 8 度音（one octave)

从C往右一个黑键，C升了半音，这个黑键叫C^#，从D往左一个黑键，D降了半音，这个黑键叫D^b

每个黑键就有两个名字了，一个升，一个降。

^，

P2 - WS= whole step (整音）  HS= half step（半音）

P3 - 一个八度音程里，有12个半音，这个是从 C 到 C，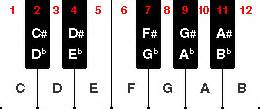

p4 - 这个是从 C-flat 到 C-flat （C^b-flat = B)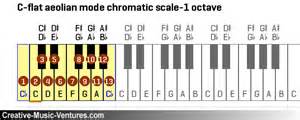

请听我演奏：Prelude＃1，C Major, Well Tempered Clavier,  Johan Sebastian Bach