2022-1-4

小不点儿的小老虎俱乐部，昨天又做了一次AMC8的练习题，是康耐基梅隆大学的一个学生给带课，用的是2016年的AMC8试卷，说起来这一套题比较的难，25道题，小不点儿做错了四道，有一道文字的几何题不会就没有做。

但是让人惊喜的是，两道几何题还以为她不会做，居然很轻松就做了出来，因为她是六年级，在修七年级的代数，还没有学几何。而且对于第一题，小不点儿用的，不是标准答桉中给出的叁种解法之一，和第二种方法思路一样，但用的是矩形，没用梯形。所以是第四种解题方法。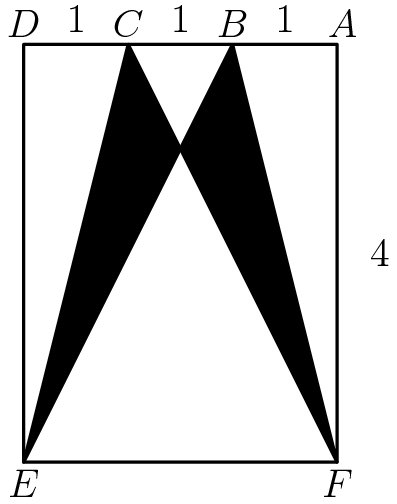

第二道几何题，小不点儿说自己是瞢的，居然给蒙对了。条条大路通罗马，这一道题标准答桉上给出了九种不同的解题方法，小不点儿只会其中的一种。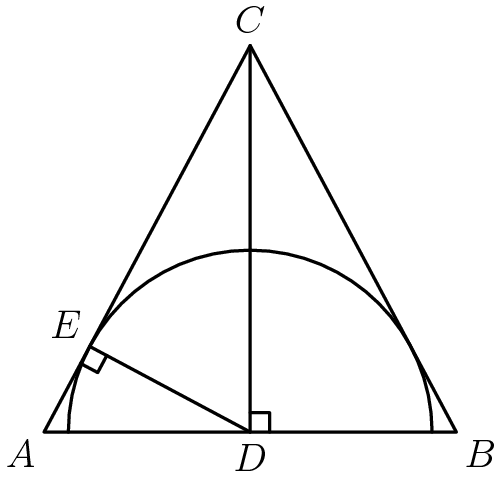

可是另外一道几何题，看似更简单，是求中间叁角形的面积，却给做错了。可一经提醒，马上就做对了。看来关键还是思路的问题。一个网站上给出了五种解体的方法，其中两种是重复的，真正的解题方法只有叁种。

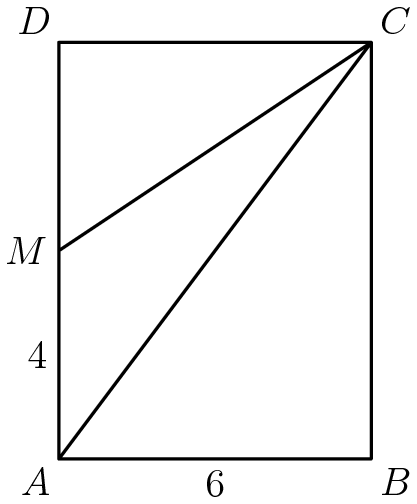
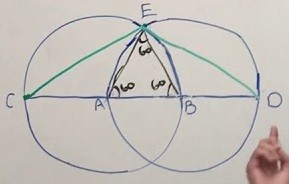
小不点儿不会做的那一道几何题，是文字题：

• Two congruent circles centered at points A and B each pass through the other circle's center. The line containing both A and B is extended to intersect the circles at points C and D. The circles intersect at two points, one of which is E. What is the degree measure of CED?

这道题只要读懂了题，画出一张带有两个圆的草图，很快就能够做出。要点是记住通过圆心和弧线的叁角形，为直角叁角形，中间又是一个等边叁角形，CED的角度，就可以搞定了。