一个星期前，我在自己的万维博客里，邀请读者做个小游戏，就是回答一个简单的数字问题： 请选择一个 0 到 100 之间的整数。如果你选择的数，最接近全体参与者的平均值的三分之二，你就是这个游戏的胜者！ （读下文之前，请您现在在心里也想一个答案。这样会使下面的阅读变得更加有趣
--） 
在万维出这道游戏题的时候，我没有给出任何的背景介绍，只是保证读者通过第三方网站送交答案，完全是匿名的，不搜集任何个人信息（包括IP地址之类）。结果是，一共收到读者提交的36个答案（少是少了点儿。其实15%的答题率，还是很不错的，可惜那贴点击率太低，众多读者错过了这个fun，我比您还遗憾）。这36个答案中，最大98，最小为0，平均值45.8，乘以2/3约等于31。最接近的一个答案是30，光荣胜出（掌声）！可惜，由于网络匿名，我也不知道答题人是谁，所以没有办法给您披红挂彩了。您知道赢了，就自己乐呵乐呵吧！ 
那位说，玩这种小儿科的猜数游戏，有什么意思啊？  您有所不知，上面这个游戏可不简单，是博弈论（Game
Theory）中的一个经典问题。博弈论是干什么的？就是研究在多方竞争对局中，面对特定条件制约，如何制定实施己方的应对策略，争取不败乃至胜出的学问。打牌、下棋、企业经营，乃至国际政治经济军事谈判，只要是有规则的竞争，样样用得上。
传统的博弈论中，有一个非常重要的公设，就是假设竞争的参与人是完全理性的，而且能够做出自身利益最优化的决策。经典博弈论的理论和模型都离不开这个前提假设。但是很显然，现实中的人是不可能完全理性的，很多时候甚至根本就是不理性的，所以在实践中，必须对这个假设进行修正。上面提出的这个猜均值问题，就可以用来验证分析个人与群体的理性程度。 按照理性人的设想，参与者应该会先排除不可能的数字。比如，即使所有的人都选择100，平均值的2/3也只是66.6666….
所以理性人不可能选择
>67的数字,
对吧。下一步，每个人的选择就变成在0-67之间选一个数，那么跟上面同样的思路，>
45的数字也成为不可能了。以此类推，不断循环下去，到最后，所有理性人的选择应该都为0，这样平均值是0，0的2/3 还是0。天下归零，举座皆赢。事实上，在万维的游戏中，确实也有一位读者交来了这个答案。Bravo，您真棒! 可是问题的关键是，只有当所有的参与者都是这样的“理性人”，才一定能得到0这个终极答案。大千世界，万紫千红，大家怎么可能都用同样的思路想问题呢？这样考虑，本身就是过于理想化的不理性了。 为了更深入地了解参与者的心态，我在单位的同事中也进行了一次同样的游戏，受邀参加者限于我常打交道的财务分析和风险分析两个部门。这次不同的是，我事先告知了参赛者的范围，设立了奖品（本人掏腰包，请喝Tim
Horton’s 咖啡一杯），而且我知道每个参赛者交出的答案，还对其中几位进行了随访。
“0。不解释。”
“13。我的幸运数字。以前在球队里的号码。”
“33。很简单，0到100 的平均数是50，50的2/3 是33。”
“67。我认为每个人来上班，都应该给出自己的100%!”（猜猜这么说话的是什么人？）
“99。办公室这帮家伙都是人精，肯定往少了猜。我偏猜个大数，给他们制造点儿麻烦！”
千真万确，这些都是我的同事们的答案。那么这个群体的游戏结果如何呢？均值29.7，乘以2/3=19.8,
胜出的答案是20，来自一位精算师。 喝着香浓的Double
Double，精算师给我讲了他的思路：“我首先猜33，再想每个人都可能会这么猜，那么就得再往下走，22或者更低。可是低到什么程度呢？我觉得财务分析那帮家伙们并不是真懂数字（huh?），想不了太深，所以就运用精算分析里的逆偏差拨备法则（provision
for adverse deviation），选了20。我这肯定算得上一个Educated guess（受过教育的头脑做出的有根据的猜测）。” 精算师显然为自己的聪明而自我感觉良好，旁边的注册会计师听了便有些不爽：“我压根儿就没认真猜！海天给的奖品太没吸引力。要是请喝星巴克拿铁嘛，我大概会多考虑一分钟。” 会计师就是这样，斤斤计较的。不过他说的激励问题，可能倒确实是一个重要的影响因素。1997年的时候，伦敦《金融时报》（Financial
Times）曾经在报上发广告，举办了一次同样的数字竞猜。当时的悬红奖品是两张从伦敦到纽约的协和飞机商务舱往返机票，市值近一万美元。这次比赛吸引了近千名读者竞猜，选得最多的数字是33，平均数是18.91，最后的赢家猜的是13。 不难想象，《金融时报》的读者应该是一群很有理性的人，面对重奖更会认真思考，但是即使如此，一个完全理性的群体也是可望而不可求的。一个理性而聪明的个人没有办法保证做出最正确的决策，因为他无法知道群体中的其他人能理性到什么程度。这便是一项没有支配性策略的博弈。 值得一提的是，当初向《金融时报》建议进行这项实验，并在自己的研究中多次提到其内涵的，是芝加哥大学的Richard
H. Thaler教授。 Thaler教授是行为经济（金融）学的创始人之一，在这个领域内与2013年诺贝尔经济学奖得主，耶鲁大学的Robert
Shiller 教授齐名。所以说这个简单的猜均值游戏，在博弈论，行为经济学和心理学中，都有着不简单的意义。 
那位又说了：“在万维做这个游戏，得到的平均值居然到达45.8，是不是说明万维的读者群很不理性啊？” 谁要是真这么想，那您可有点犯糊涂了。 首先，上次参加的人太少，这么小的样本什么都说明不了； 其次，出现大均值，是因为其中有几个>>67的答案。想想大家上网时的状态，娱乐为主，看什么有一搭没一搭的，题目或许都没仔细看，太正常了。当然也不排除有存心捣乱的，像我的第五位同事那样； 第三，也有数目相当的读者，选择的答案<<30。这样的读者长于理性思考，是群体中宝贵的思想者； 第四，也是最重要的一点：收到的答案中，最多的一组分布于30～35之间 。这充分证明我们万维的读者，大多数是正常人，对所属的人群有一定的了解和敏感度，但也忠于自己的内心，游走于理性与感性之间，进退有度。 洋洋洒洒，居然写了这么多。读到这里，想必每一位读者都对这个游戏有了一个更加理性的认识。大家想想看，如果咱们现在把这个游戏重玩儿一遍，结果会怎么样呢？面对一群理性的万维读者，聪明的你如何把握群体心理，最后胜出？！ 好吧！以前的结果清零，游戏重新开始，请发出你的答案吧！ 截止时间：2013年11月9日(周六）GMT 23:59(EST 18:59)。
声明：信誉保证，完全匿名 （当然，您留言作答也没问题）。
奖励：能精准把握群体的理性预期与心理，并作出相应的决策 – 您都有这样的本事了，还需要什么奖励啊？！
结果公布： 感谢各位，本次共收到54个答案； 均值20.98，所以最接近均值2/3的答案为14；
共有3位网友选择了这个答案！祝贺您！ 对比两次结果，我们可以感受人群是由有限理性的行为主体构成的，因此对所谓的最优策略均衡点会总有相当程度的偏离和发散；在理性认知回归的同时，群体行为也必将向均衡点稳定收敛。 下图为所收到答案的时间序列：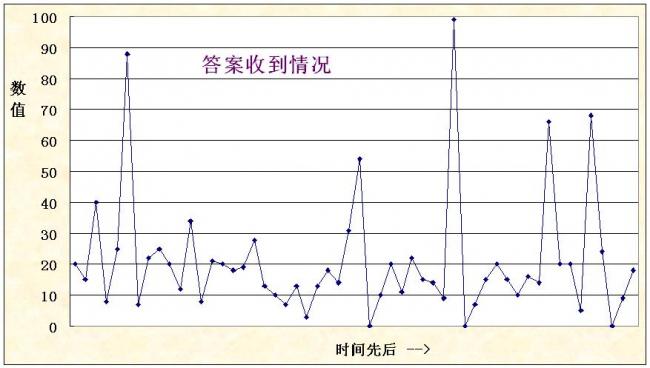 
图2为收到答案的分布情况：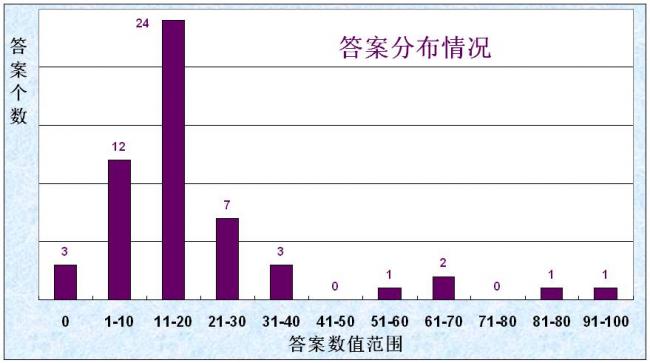 
祝各位周末愉快！
|
