数学及其应用 几乎所有的数学都源于应用问题,但时代久远之后,人们往往忘掉了。比如说,几何学,是一门纯数学,但几何学 (geometry) 的意思是测地学,显然源于应用问题。对应用问题的理解,很大程度上决定了数学和科学的发展方向。下面我们用拓扑和分析在经济学领域的应用来分析一下。 很多人都看过一本叫做《美丽心灵》的书,或者根据此书改编的电影。此书的主人公叫纳什,他建立了博奕论中一个重要的结果,用的是拓扑学的方法。主流经济学理论的基础是一般平衡态理论,其严格的数学证明,也是建立在拓扑学基础上的。可以说,拓扑学为主流经济学理论提供了严格的数学基础,但这是不是一个合适的基础?经济问题是数字问题,一件货物,如果成本是100块钱,卖了110块钱,就能盈利,卖了90块钱,就会亏本。但是从拓扑学角度,90 ,100 ,110是没有区别的,所以拓扑学不能表达经济学和生物学中最根本的特征,追求非负的投资回报率。可是由于拓扑学理论简单,早期的数理模型往往源于拓扑学。 价值理论是经济学理论的基础。主流经济学价值理论叫做Arrow-Debreu 理论[1], 为此Arrow 和 Debreu两人都拿了诺贝尔奖。这个理论也是采用拓扑学方法,不能提供一个定量的分析。而对数函数的方法则对决定经济价值的因素提供了清晰的分析。我们来具体了解一下。 在一个新的价值理论里 [2], 物品的价值定义为 -logbP 其中 P 为物品的稀缺程度,范围从 0 到 1, 0 为极度稀缺, 1 为无限丰富,b 为这个物品的生产厂家数目。我们来看一下这个函数的性质。 首先,一种物品的价值是稀缺程度的递增函数,物品越丰富,其价值越低,如果这种物品无限丰富,也就是P = 1,其价值为零。比如说,空气对我们非常重要,几分钟不呼吸,我们就活不下去。但由于空气无处不在,其经济价值为零。下图是价值与稀缺程度之间的关系。 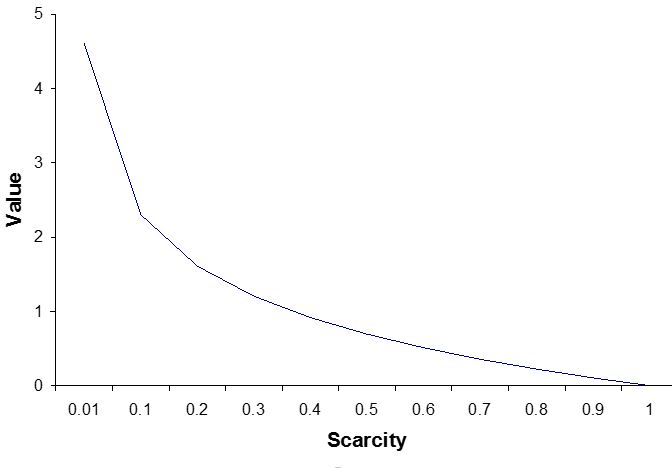
很多人把经济价值等同于对社会的贡献。当今粮价很低,很多人认为农民对社会的贡献低。但如果粮食太贵,有人买不起,很快引发社会动乱。所以很多国家的政府采取各种政策,以保证粮食的充足,同时也造成粮价低廉。很多政府为了保护农民利益,大量补贴农民。从这个价值理论,我们可以清楚看到,经济价值不等同于对社会的贡献。 我们再来分析生产厂家的个数对价值的影响。b 越小,物品的价值越高,下图是物品的价值与生产厂家数目的关系。一样物品,生产的厂家越少,价值越高,大家都知道垄断和寡头经营的行业,利润很高。这个分析不仅可以应用到产品上,也可以应用到任何社会系统,世界上影响力大的宗教,象犹太教,基督教,伊斯兰教,大多是一神教,而佛教和大多数早期的宗教,是多神教,一神教对教徒的控制能力比多神教强很多,当一神教碰到多神教的社会,往往会击败对方。很多职业收入高,往往是由于这些职业由唯一的组织代表。比如说,加拿大所有的医生,都属于同一个医学学会,没有任何竞争;加拿大医生的收费,是统一的,也没有任何竞争;病人看病,必须通过唯一的家庭医生,彼此之间没有竞争。这就是为什么加拿大医生的地位,比中国高很多。我们经常说西方经济是自由竞争的市场经济,但其中最重要的部门,象医疗,教育,军工,以及庞大的政府本身,都由工会和垄断机构控制,很少自由竞争。 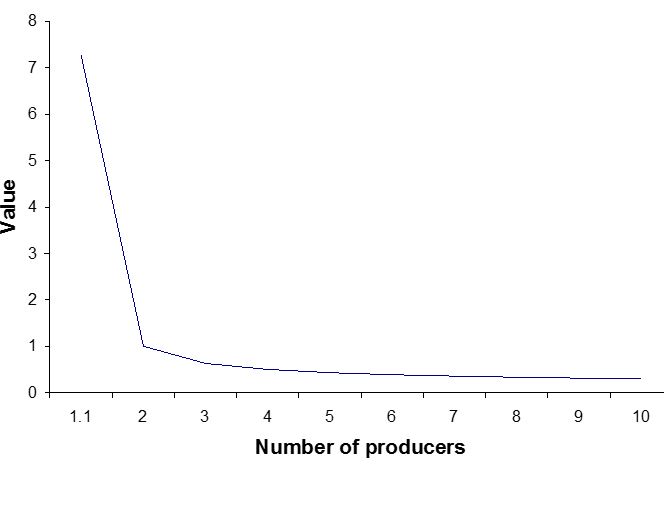 减少选择,对增加价值有决定性的影响。所以几乎所有经济,政治活动,都以减少竞争,增加垄断权力为目的。我们常说的专利法和知识产权保护就是一个例子,知识产权保护最常用的理论是鼓励创新,但创新最多,给消费者带来最多利益的行业,象信息技术,往往是知识产权最自由的行业,而知识产权保护最严格的行业,象生物医学,往往是纳税人花大钱,消费者受益甚少的行业。 从上面的讨论,我们看到,一个简简单单的对数公式,可以帮助我们深刻了解这个社会中形形色色的活动。很多原本不喜欢数学的学生,也很开心学到对数函数的各种性质。关于这个公式更多的应用,可参看价值的熵理论[2]。
经济学的拓扑理论最初建立于半个多世纪之前,这些早期的探索者值得我们尊敬,但是,拓扑学理论没有能够把实际经济活动中重要的因素表达出来,而分析理论则可以。
拓扑学理论是数学的主流,另一门数学的主流是代数几何。代数几何是关于多项式函数的几何理论,多项式自然古老,多项式自然重要。但大多数重要的物理问题,生物问题和社会问题包含指数函数和对数函数,所以代数几何的研究不涉及很多自然界最基本的问题。
自然现象发生在空间和时间之中,自然现象的变化涉及几个变量的变化,所以,偏微分方程应该是描述自然现象最基本的方法。确实如此,过去一百多年,科学理论的重大突破,大都表现在偏微分方程的提出,象麦克斯韦方程,薛定谔方程,Black-Scholes 方程。而这些偏微分方程的解,大都不是多项式函数。如果一直把代数几何作为数学的中心,主流的数学研究就越来越偏离自然界最根本的问题。
我们很多人对数学的现状,科学的现状,经济学的现状不满意。但是要改变这种状况,需要我们的积极参与,把好的数学方法引入经济学研究,把重要的经济学问题引入数学研究。只有这样,数学这棵老树,才能开出绚烂的新花。
具体一点,我们用电磁波谱作一个比喻,从无线电波到伽马射线,但是给人们带来最多信息的是人们熟悉的可见光。同样,从拓扑学到代数几何,数学方法从一般到具体,拓扑学太一般了,生命科学和经济学中所需要的定量化往往不能表达,而代数几何限制过多了,生命科学和经济学中最常出现的对数函数和指数函数被排除在外。我们最需要的是普通的分析理论,就像我们在日常生活中,最需要的是普通的可见光一样。
在众多分析理论中,我们进一步聚焦到两个问题,对数函数和费曼-Kac 公式。熵定律是物理界最普遍的规律,熵的不断增加,是所有生命的动力,而熵的数学表达式是 S= k log W 所以对数函数自然是生物学和经济学中最重要的函数。
自然界中充满了不确定性,我们对世界的判断是一个求平均值的过程。而费曼-Kac 公式提供了一个求平均值的普遍方法,把费曼-Kac 公式应用到生物学和经济学领域,将极大提高我们对这个世界的认识 [3]。
参考文献 1. Debreu, G. (1959). Theory of value; an axiomatic analysis of economic equilibrium. New York: Wiley. 2. Jing Chen, An Entropy Theory of Value: Forthcoming in Structural Change and Economic Dynamics https://www.researchgate.net/publication/228398386_An_Entropy_Theory_of_Value 3. Jing Chen, The Unity of Science and Economics: A New Foundation ofEconomic Theory, (2016), Springer
下面是一篇关于数学及其在社会科学中的应用的通俗介绍。
|
