大部分流行的经济学理论是平衡态理论,这些理论认为社会系统会不断趋向最佳平衡态。比如说,马克思主义认为全世界会演化到共产主义这个最高阶段,而当今西方的主流理论,新古典主义经济学则认为全世界会演化为自由市场经济,前些年有本很轰动的书,叫《历史的终结》,就是这个意思。这些平衡态理论有什么特征?
在这些理论中,最佳状态是一种主观的定义。有人把吸毒带来的短期幸福感定义为最佳状态,按照这种定义,即使全社会的人都在吸毒也不是问题。由于最佳状态是一种主观定义,实际上精英阶层的价值观就成为整个社会的标准。比如说,现在主流社会对清洁能源极为追捧,但清洁能源的生产,象太阳能发电版的生产,电池的生产,带来巨大的污染。可是清洁能源的制造集中在中国,清洁能源的使用集中在西方,所以制造过程中的污染极少引起精英阶层的兴趣。
和社会理论不同,自然科学理论认为生命系统,包括人类系统是非平衡态系统,而平衡态则代表死亡。当然,自然科学理论中的平衡态和社会科学理论中的平衡态不是同一个概念,我们想要知道的是,哪一个理论更能对社会现象做出简单,清晰的理解。
市场是经济学中一个极为重要的概念。在主流经济学理论里,市场竞争使社会趋于最佳状态,但市场经常出现外部性 (externality), 所以需要政府干预。可市场到底有多少外部性,谁也说不清楚,主流经济学从来没能清晰表达政府和市场的关系。
平衡这个词有很多解释,非平衡这个词也有很多解释,我们选取物理学中的解释。我认为生命现象和社会现象就是物理现象,而非仅仅是类似于物理现象。从非平衡态理论,一个系统离平衡态越远,其工作效率越高,但系统的制造成本和维持成本也越大。一个水坝,建得越高,发电越多,但是建造水坝的成本也越高。一个输电系统,电压越高,途中的损失越少,但是变电站的制造成本也越高。一个商店,处在闹市,销售量很高,同时租金也很高。一个人的学位越高,平均工资越高,但前期投资也越大。从经济学的角度,要降低系统的可变成本,必须增加固定成本。而具体如何选择固定成本和可变成本,应该着眼于投资的正回报。这一点,在公司的投资中是十分清楚的,但对于整个社会,或者说是宏观经济学,却十分模糊。 人类社会,首先是个生物社会,如果生育率持续低于替换率,人口不断老化,这个社会必定会走向衰亡,日本就是一个典型的例子。日本的生育率,在七十年代初就已经跌落到替换率之下,如果在那个时候就采取措施,日本就不会处于今天的绝望状态,那么应该采取什么措施呢?我们先来观察一下,一个生态系统中不同的物种。 一个生态系统中,有的动物很大,像棕熊,有的动物很小,像松鼠。我们往往觉得,越大的动物就越有优势,确实,大动物往往个体寿命较长,但物种寿命较短。越大的动物,固定成本越高,生育率越低。由于大动物需要很多资源,难以在逆境中生存。而小动物,固定成本低,生育率高,尽管个体非常弱小,但需要的资源少,常常在逆境中得以生存。作为物种,小动物的寿命反而更长。 从上面的讨论,我们得知,固定成本越高,生育率越低。目前大部分西方国家,生育率已经连续几十年低于替换率,人口不断老化,社会趋于衰亡,而不是平衡态理论所宣称的最佳状态。要扭转生育率低迷的状况,必须要降低固定成本,具体到政策上,就是降低税收,降低或废除公积金。当然,这样做的阻力很大,加拿大政府不久前还增加了公积金,使处于育龄的年青人的负担进一步上升,尽管加拿大的生育率已经非常之低。纵观历史,大多数高度发达的国家,最终都是被发展程度低得多的部落所征服,而非内部改革成功。 非平衡态理论在物理上非常直观,让我们推导出一个生产过程的数学理论,这个数学理论不仅包括固定成本和可变成本,还包括生产过程中其他几个重要因素,折现率,投资期限或生物寿命,不确定性,和市场大小。从这个定量理论,很容易考察各个因素之间的相互关系,而这是一个定性理论很难做到的。我将在附录中简单介绍这个数学理论的推导思想,详细的推导请看我的书和文章。下面,我们再来对比一下平衡态和非平衡态理论的特征。 平衡态理论,简而言之,就是:道路是曲折的,前途是光明的。如果我们处于一个上升的社会,这样的理论,给予我们无穷的激励。但当我们处于一个下降的社会,这样的理论却使我们盲目乐观。欧洲,日本,从七十年代开始,人口出生率已经低于替换率,可这些地方仍然一直追求经济增长,导致人口老化问题日益严重。一个社会不可能永远生机勃勃,怎样尽早察觉自己的弱点,并做出有利于社会长期利益的调整,就是这个非平衡态理论的功能。
具体来说,当一个社会的生育率低于替换率,首先应该降低这个社会的固定成本,这包括降低税收,减少学校的教育年限等很多措施。同时,利率,市场规模等其它因素也对固定成本的选择产生影响,对这些因素的确定,非平衡态理论给出了明确的答案。通常这些答案都和现行的政策相反,这是非常自然的,因为大多数现行的政策着眼于短期的利益。政府往往降低利率以刺激经济,尽管很多人都明白低利率政策很可能在将来造成金融危机。统一的欧元,在短期内增加了市场规模,降低了贸易的成本,但长期后果是,使各国丧失了处理经济问题的灵活性。这个非平衡态理论的数学理论使我们更容易看到不同政策的长期后果,使我们更容易在短期和长期之间做出选择。
附录:非平衡态理论经济学的数学理论的推导过程。 理解生命现象的关键,是认识到生命现象是物理过程和经济原则的综合体,我们所说的自然选择,加以量化,就是回报率大于零,从经济学角度,是产值高于成本,从生物学角度,就是摄取的资源高于消耗的成本。
生物学和经济学的一般规律应该包括两条。首先,所有生物或经济体都需要吸收外部的资源来补偿自身的耗散,第二,从外界得到的资源必须要高于成本,包括固定成本和可变成本。下面我们将这两条规律转化为数学理论。
吸收资源以补偿自身的耗散,这可以用对数正态过程来表达,
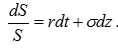 第一项是吸收项,第二项是耗散项。由于我们关注的是平均值,而非随机分布的每一点,我们可以将随机过程转化为相对应的确定性方程。转化方法有很多种,我们采用量子力学中的费曼路径积分方法,这是因为量子力学的方法就是加权平均,而在生物学和经济学中,我们需要折现,费曼-Kac 公式正好提供了加权的方法。当然,还可以从物理角度解释,生命现象就是量子现象,所以用量子力学的方法是自然的。
利用费曼-Kac 公式得到代表生命过程的热力学方程是 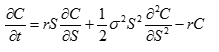
我们需要初始条件才能解这个方程。我们把初始条件设成资源量等于固定成本加可变成本,这是生命存在的边界条件。如果固定成本低于所摄取的资源,可变成本是资源和固定成本之差,如果固定成本高于所摄取的资源,就不再需要额外的可变成本。让 S 代表资源量, K 代表固定成本, C 代表可变成本,数学上,这就是
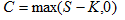
有了这个边界条件,我们就可以解出这个方程,其中的时间值 T 代表生命的长度(lifespan), 或投资的期限。恰好可以得到如下的解析解,
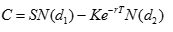 (1) (1)
其中

而 N(x) 是标准正态分布随机变量的累积概率函数。也就是说,可变成本可以表达成资源量,固定成本,生命长度或投资期限,耗散率或者不确定性,和折现率的解析函数。熟悉金融工程的读者,会看到这个公式和 Black-Scholes 公式的形式一模一样,但各个参数的经济意义是不一样的。
有了这个可变成本的解析公式,我们可以进一步计算各种投资的预期回报。假设整个投资期间的产出量是 Q,单位产品的价值和可变成本分别为 S 和 C, 则总收入和总成本分别 SQ 和 K + CQ
投资的净现值为 SQ - (K+ CQ) (2)
投资的回报率为
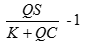 (3) (3)
我们经常用 S 代表单位时间的产出, 如果投资项目的期限是 T, 那么, 投资的净现值为 ST - (K+ CT) (4)
投资的回报率为
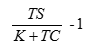 (5) (5)
有了这个生产过程的解析理论,就可以推演出经济学和生态学中很多现象。我们先来计算在不同大小的不确定性环境下,固定成本增加时,对可变成本的影响。从公式 (1),计算结果如下图。
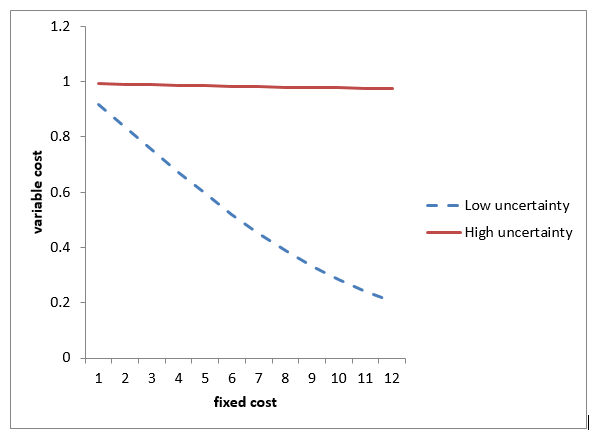
这个计算非常容易,用简单的 Excel 就能完成,所用的 Excel 文件放在文章最下面,可以自己下载,自己做各种运算。上图的计算放在 Sheet1.
上图的计算显示, 高固定成本的投资在低不确定性的环境下能显著降低可变成本, 而低固定成本的投资在高不确定性的环境下更具灵活性。在生态学里,物种分类为低固定成本的r类物种和高固定成本的K类物种,在波动幅度很大的环境,r类物种 (r species) 有优势,在稳定的环境里,K 类物种 (K species) 占统治地位。从上面的计算,当耗散系数很大,代表环境变化很快,无论如何提高固定成本,很难降低可变成本,在这种环境下,低固定成本的r类物种占优势。当环境稳定(耗散系数低),提高固定成本可以迅速降低可变成本,在这种环境下,高固定成本的K类物种占统治地位。
同样,在变化很快的经济领域,技术往往由一两个人创造的新公司引领,象苹果,微软,网景,雅虎,谷歌,脸书,往往是几个年轻人建立的,而成熟的领域,象消费品行业,往往是象可口可乐,宝洁这种老牌企业称雄。在科学研究中,成熟的领域往往由名校的大牌教授领导,而革命性的理论往往源于新人或局外人。
我们再来计算不同固定成本的投资,在不同的产出或市场大小情况下的回报。从公式 (3),计算结果如下图。下图的计算放在 Excel 文件的Sheet2.

从上图可以看到,高固定成本的投资需要较大的产出才能回本,同时,由于高固定成本的投资可变成本低,其回报曲线较陡,在大市场中可以取得高回报。而低固定成本的投资则相反。
产能过剩是经常讨论的一个问题,产能过剩,本质是生产系统的固定成本过高,需要大量生产才能保本。为什么固定成本过高?这主要是因为预期的经济增长速度过高,公司,或者政府,选择高固定成本的生产系统,期望在将来的大市场中获得高回报。如果经济增长速度不再成为政府的考核因素,产能过剩的问题应该很快能解决。
我们接下来讨论人们在不同环境下的投资决定。在给定的条件下,人们会选择特定的投资方式以得到最大的回报率或净现值。我们假设不确定性是环境条件,是我们不能改变的,而固定成本和投资期限是我们自己可以调节,控制的。在 Excel 中,有一个 add-in, 叫 solver, 可以用来解决极值问题。在不同的不确定性下,我们以固定成本和投资期限为变量,用solver 来寻求净现值,即公式 (4)的最大值,计算结果放在Excel 文件的Sheet3. 大家可以看到,当不确定性低的时候,固定成本高和投资期限长,净现值高,当不确定性高的时候,固定成本低和投资期限短,净现值低,这是大多数人喜欢稳定的环境的原因。
在一个稳定的社会环境,大多数人的固定投资很高,尤其表现在教育方面,高等教育十分普遍,在一个不稳定的社会环境,象处于战争状态的地区,大多数人的固定投资低,读书的年数少。通常我们觉得,固定成本高和投资期限长是好事,但如果我们所在的地区, 突然变得很不稳定,从Sheet3上的计算,固定投资越高的系统损失越大,这就是为什么在社会大变动的年代,那些简单的社会系统和底层的人反而能够生存,在地质大变动的时代,那些处于统治地位的大物种,象恐龙,会灭绝,而简单的物种反而能够生存。
货币政策和商业周期是经济理论和政策中的重大问题,我们来考虑货币政策和商业周期的关系。降低利率能够增加资产和公司的价值,所以政府经常选择低利率,特别当经济衰退的时候。但是长期的低利率政策容易造成经济活动的大幅波动,这经常归咎于低利率造成的通货膨胀。还有别的原因吗?我们来计算一下高利率和低利率环境下的投资行为。计算结果放在Excel 文件的Sheet4. 大家可以看到,当利率低的时候,固定成本高和投资期限长,净现值高,当利率高的时候,固定成本低和投资期限短,净现值低。也就是说,货币政策不仅影响资产价值和经济产出的数量,更重要的是投资的结构。如果我们所在的社会,突然变得很不稳定,从Sheet4上的计算,固定投资越高的系统损失越大,也就是说,利率越低的社会,商业周期的幅度越大。大多数政策制定者知道这个道理,但是,人们通常对低利率的短期好处有清晰的理解,对低利率的长期问题则较少考虑,导致利率在低处停留过长。我们的计算,非常简单,使低利率的长期问题很容易理解。
人们曾用不同的数学方法描述生物进化和经济学过程,象福柯-普朗克方程、柯尔莫哥洛夫扩散方程。我们来讨论一下费曼-Kac 公式和其它方程的关系。费曼-Kac公式是柯尔莫哥洛夫backward 方程的推广,而福柯-普朗克方程是柯尔莫哥洛夫forward 方程。我们研究的时候,可能会尝试很多的方法,大部分方法都无功而返,只有少数能够成功。当我们登上山巅,再往下看,应该走的捷径往往一清二楚,但是在山底下的时候,往往很难看清楚。
更具体的分析,请参考
Chen, J, The Unity of Science and Economics: A New Foundation of Economic Theory, (2016), Springer
Excel 文件 �http://web.unbc.ca/~chenj/Examples.xlsx �
|
