进化理论的数学模型 前几天读到胡大伟先生的一篇博文,文章不长,贴在下面。 进化很好理解,但怎么用数学模型来表达呢?胡大伟 这些年,我一直在想下面的问题,并把它向很多外国大理论生态学家提出,可他们的回复都是 I don't know。 Although it is very easy to intuitively understand Darwin's theory of evolution, i.e, ever increase complexity of system structure sustained by matter, energy and information connections for acclimation, I think that there is a more enormous challenge on how to express it by mathematical models whose analytical expression must also be changed along with time. For example, suppose that at t moment,the kinetic model of a specific ecosystem could be written as follows: dx/dt= f(t)(t,x,p,u) = 3*x*u- 2*exp(-x) wheret x, u is state and input, respectively. but at t+△t moment,it maybe changed by eco-work during △t into new analytical expression as follows: dx/dt= f(t+△t)(t,x,p,u) = x^2-2*exp(-2*x)+u*exp(x) If we can solve this huge problem, really valid ecological models would be developed to describe and predict the ecosystem behaviors, such as the species origin, community succession, niche differentiation, ecosystem evolution, and so forth. 这个问题不解决,近5年来,我所建立的生态学模型都很naive,因为和所有建模者一样,把生态系统看成了机械系统,没有触及它的根本动力学机制。生态系统的变化不是量变,而是质变,我理解质变就是结构的复杂化。 ~~~~~~~~~~~~~~ 现在,生态系统的标准模型是常微分方程,这在他的博文中也可以看到。我在他的博文后面留言,“生命现象是热力学现象,应该用热力学方程描述。” 他回答,“我可以毫不犹豫地说,传统的热力学定律和方程根本无法描述生命运动。热力学必须有最原始的创新,就像牛顿发明导数那样的创新,才有可能把数学用在描述生命现象之中。” 他说得很对,早期的研究者都知道生命现象是热力学现象,应该用热力学方程描述。正是由于没找到适当的热力学方程,才用更简单的常微分方程建模。我们从最原始的角度,看一下生命运动的根本特征。生命运动的根本特征应该包括两条。首先,所有生物都需要吸收外部的资源来补偿自身的耗散,第二,从外界得到的资源必须要高于成本,包括固定成本和可变成本。我们所说的自然选择,加以量化,就是回报率大于零, 就是摄取的资源高于消耗的成本。下面我们将这两条特征转化为数学理论。 这个理论的推导确实不容易,但是最终的结果是个解析解,非常简单。理论推导出来后,我们用它来解释 species origin, community succession, niche differentiation, ecosystem evolution, and so forth.
吸收资源以补偿自身的耗散,这可以用对数正态过程来表达, 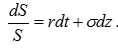 第一项是吸收项,第二项是耗散项。由于我们关注的是平均值,而非随机分布的每一点,我们可以将随机过程转化为相对应的确定性方程。转化方法有很多种,我们采用量子力学中的费曼路径积分方法(费曼-Kac 公式),这是因为量子力学是最普遍的求加权平均的方法。
利用费曼-Kac 公式得到代表生命过程的热力学方程是
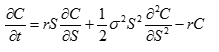
我们需要初始条件才能解这个方程。初始条件就是我们常说的自然选择的量化。具体一点,我们把初始条件设成获取的资源量等于成本,固定成本加可变成本,这是生命存在的边界条件。如果固定成本低于所摄取的资源,可变成本是资源和固定成本之差,如果固定成本高于所摄取的资源,就不再需要额外的可变成本。让 S 代表资源量, K 代表固定成本, C 代表可变成本,数学上,这就是
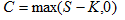
有了这个边界条件,我们就可以解出这个方程,其中的时间值 T 代表生命的长度(lifespan), 或投资的期限。恰好可以得到如下的解析解, 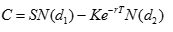 (1) (1) 其中 
而 N(x) 是标准正态分布随机变量的累积概率函数。也就是说,可变成本可以表达成资源量,固定成本,生命长度或投资期限,耗散率或者不确定性,和折现率的解析函数。熟悉金融工程的读者,会看到这个公式和 Black-Scholes 公式的形式一模一样,但各个参数的经济意义是不一样的。 固定成本可以看成系统复杂性的量化标志。 有了这个可变成本的解析公式,我们可以进一步计算各种投资的预期回报。假设整个投资期间的产出量是 Q,单位产品的价值和可变成本分别为 S 和 C, 则总收入和总成本分别 SQ 和 K + CQ
投资的净现值为 SQ - (K+ CQ) (2)
投资的回报率为
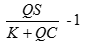 (3) (3)
我们经常用 S 代表单位时间的产出, 如果投资项目的期限是 T, 那么, 投资的净现值为 ST - (K+ CT) (4) 投资的回报率为 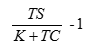 (5) (5) 有了这个生产过程的解析理论,就可以推演出经济学和生态学中很多现象。我们先来计算在不同大小的不确定性环境下,固定成本增加时,对可变成本的影响。从公式 (1),计算结果如下图。
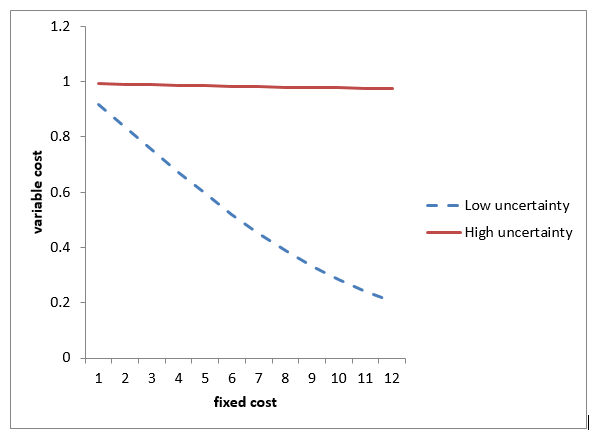 上图的计算显示, 高固定成本的投资在低不确定性的环境下能显著降低可变成本, 而低固定成本的投资在高不确定性的环境下更具灵活性。在生态学里,物种分类为低固定成本的r类物种和高固定成本的K类物种,在波动幅度很大的环境,r类物种 (r species) 有优势,在稳定的环境里,K 类物种 (K species) 占统治地位。从上面的计算,当耗散系数很大,代表环境变化很快,无论如何提高固定成本,很难降低可变成本,在这种环境下,低固定成本的r类物种占优势。当环境稳定(耗散系数低),提高固定成本可以迅速降低可变成本,在这种环境下,高固定成本的K类物种占统治地位。 同样,在变化很快的经济领域,技术往往由一两个人创造的新公司引领,象苹果,微软,网景,雅虎,谷歌,脸书,往往是几个年轻人建立的,而成熟的领域,象消费品行业,往往是象可口可乐,宝洁这种老牌企业称雄。在科学研究中,成熟的领域往往由名校的大牌教授领导,研究的规模庞大,而革命性的理论往往源于新人或局外人,由一两个人完成。 这解释了 niche differentiation。 我们再来计算不同固定成本的投资,在不同的产出或市场大小情况下的回报。从公式 (3),计算结果如下图。 
从上图可以看到,高固定成本的投资需要较大的产出才能回本,同时,由于高固定成本的投资可变成本低,其回报曲线较陡,在大市场中可以取得高回报。而低固定成本的投资则相反。
在一个新的生态环境中,比如说由于滑坡,环境营养缺乏,不稳定性高,从上图可以看到,低固定成本的生命容易存活。当环境营养不断积累,系统趋于稳定,高固定成本的生命更有竞争力,逐渐统治生态环境。
这解释了 community succession, and ecosystem evolution. 不同的环境,需要不同的固定投资,这就是 species origin 的原因。
我们接下来讨论人们在不同环境下的投资决定。在给定的条件下,人们会选择特定的投资方式以得到最大的回报率或净现值。我们假设不确定性是环境条件,是我们不能改变的,而固定成本和投资期限是我们自己可以调节,控制的。在 Excel 中,有一个 add-in, 叫 solver, 可以用来解决极值问题。在不同的不确定性下,我们以固定成本和投资期限为变量,用solver 来寻求净现值,即公式 (4)的最大值,大家可以看到,当不确定性低的时候,固定成本高和投资期限长,净现值高,当不确定性高的时候,固定成本低和投资期限短,净现值低,这是大多数人喜欢稳定的环境的原因。
在一个稳定的社会环境,大多数人的固定投资很高,尤其表现在教育方面,高等教育十分普遍,在一个不稳定的社会环境,象处于战争状态的地区,大多数人的固定投资低,读书的年数少。通常我们觉得,固定成本高和投资期限长是好事,但如果我们所在的地区, 突然变得很不稳定,可以计算出,固定投资越高的系统损失越大,这就是为什么在社会大变动的年代,那些简单的社会系统和底层的人反而能够生存,在地质大变动的时代,那些处于统治地位的大物种,象恐龙,会灭绝,而简单的物种反而能够生存。 更具体的分析,请参考 Jing Chen and James Galbraith, A Biophysical Approach to Production Theory, Working paper
|
