Entropy: In intuitive Introduction Entropy law is the most universal law in nature. Entropy must be very relevant to our life. Indeed, we frequently use this concept in our writings. However, we often don’t feel comfortable with this concept. What is entropy? In short, entropy is probability. If so, why don’t we just say probability? Why do we create another term? Entropy is in a sense a total probability. What does that mean? If we say there is a 30% chance raining tomorrow, there is also a 70% chance not raining. When we talk about entropy, we will put both probabilities together. If so, everything adds up to 100%. Why would we even bother? Suppose in one place, there is 50% chance raining everyday, 50% chance not raining. In another place, there is 1% chance raining everyday, 99% chance not raining. The situation can be very different. When there is 50% chance raining, you probably will prepare for raining everyday. When there is only 1% chance raining, you probably won’t prepare for raining at all. That is where entropy comes into use. In the first case, we say entropy is high. In the second case, we say entropy is low. One way to think about entropy is uncertainty. When there is 50% raining, 50% not raining, uncertainty is high. Actually, this situation has the highest uncertainty. When there is 1% raining, 99% not raining, uncertainty is low. Most of time, we prefer less uncertainty, or lower entropy. Entropy not only gives a qualitative concept, but also a quantitative measure. Let’s return to the raining, not raining case. Suppose the chance of raining is p, chance of not raining is q. p+q = 1. Then the entropy of the situation is p*(-log p)+q*(-log q) Now you see a math formula, you see a log function. You want to quit. Don’t! You are going to understand the most important concept in the world, the most important concept in the universe. p and q are the probabilities of two events (rain or not rain). -log p and -log q are the values of these probabilities. What does value of a probability mean? Suppose it rains often in a place. If weather man on TV says it is going to rain tomorrow, it is really no big deal. You are well prepared anyway. Suppose it rarely rains in another place, If weather man on TV says it is going to rain tomorrow, it helps a lot. You can put off your camping trip to another day. The graph of – log p looks like this. 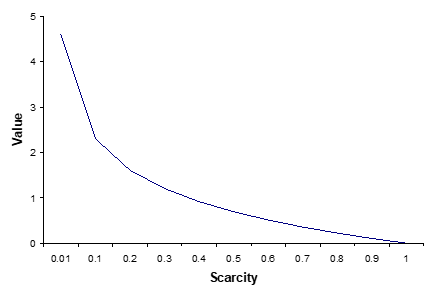
If the probability is 1, -log 1 = 0. The value of this information is zero. You already know it anyway. On the other hand, if the probability is very small, the value of information is very high. You might say. All this look nice. But what’s the big deal? We call our age information age. A big milestone of information age is the publication of Shannon’s information theory in 1948. What is in that paper? The most important result is his definition of information as entropy. I = p*(-log p) +q*(-log q) Why is this result important? Let us look at the graph of this function.
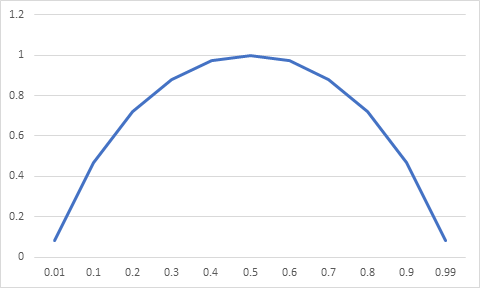
You find that when p is around 0.5, information cost is very high. When p is around 0.01 or 0.99, information cost is very low. That is natural. When p = 0.01, there is not much uncertainty. Shannon’s formula gives the lowest possible cost for information transmission. Why is this formula so important? Now you are watching a movie online. How is it possible to transmit so much information so fast? This is because in movie, the difference in consecutive pictures is very small. In other words, the uncertainty level is very small. From the above graph, you can transmit information at a very low cost. Usually, a movie file can achieve one hundred times compression because of coding. You don’t mind one second delay in movie. But one hundred second is a long time to wait. Information theory is a great help in information age. The main result of information theory is to define information as entropy. You might say. This is very useful. But this is far from being fundamental and universal. What is entropy? Entropy is essentially probability. The world is moving from a low probability state to high probability state. In formal jargon, the world is moving from low entropy state to high entropy state. This is the entropy law, or the second law of thermodynamics. This is the most universal law in the nature. But why is this law important to our life? Many of us have visited hydro dams. The water levels at both sides of a dam are different. This difference generates the tendency for water to flow from one side to another. This directional flow can generate electricity and other useful energy. In general, the entropy flow generates most of the directional flows in this world. All living systems, including human beings, owe our life to entropy flows. Entropy flow is the fountain of life. This understanding is the opposite of entropy as a symbol of death. The concept of entropy is vital to understand life and human societies. Because the concept of entropy is so universal, many prominent economists tried to apply it in economic analysis as well. However, early attempts don’t always yield fruitful results. When this happened, their attitude towards entropy became very negative. Paul Samuelson, the most powerful economist of our time, once stated, And I may add that the sign of a crank or half-baked speculator in the social sciences is his search for something in the social system that corresponds to the physicist’s notion of “entropy”. Few want to be a crank or half-baked speculator. Modern economic theory has since largely detached from physics in general and entropy in particular. But our life is intricately connected to our physical environment. An economic theory that is detached from physical foundation has flamed out for a long time. We need some cranks to crank start the engine again. In Shannon’s information theory, the value of information is defined as -log2 (p) The base of the logarithm is two. This is because information is transmitted through a binary system {0, 1}. In economic activities, there can be a number of producers making the same product. We can define the value of economic product to be -log b (p) Here b is the number of producers. Value of a product is the function of scarcity and the number of producers. We have already seen the graph how value changes with scarcity (probability). Now we draw a graph to show the relation between value and number of producers. 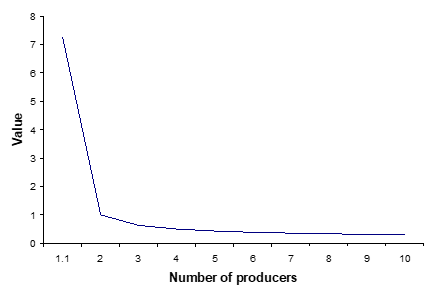
When the number of producers approach one, the value of the product approaches infinity. This is the value of true monopoly. This is why governments, the most dominant social organizations, are organized as monopolies. This is why most highly paid workers are unionized so they will have monopoly power in bargaining. This is why most successful religions are monotheistic. Indeed, to achieve and maintain monopoly is the strongest motivation in many human activities. As we have seen, entropy function, a logarithm function, is very simple. Yet it contains many fascinating properties that influence our life profoundly. For more detailed discussion about entropy, you might want to read Jing Chen, 2015, The Unity of Science and Economics: A New Foundation of Economic Theory, Springer
|
