数学:应用和乐趣 (修订版) 大部分学生不喜欢数学,觉得数学没用,大部分数学老师也讲不出数学有什么用。一般来说,乐趣和有用连在一起,所以,家长和老师都希望找到介绍数学有用的文章。但这类文章,讲数学如何的有用,举的例子很多是二次世界大战期间,数学家如何神武,为盟军胜利立下汗马功劳。二战过去七十多年了,作者怎么举不出新一点的例子呢?类似的文章很多,一谈到数学的好处,就是如何训练思维,如何潜移默化,拐弯抹角讲了半天,一提到应用,要么是很难的数学,象天气预报,要么是很遥远的应用,象黑洞。难道没有简单的数学,能够应用到日常的生活? 有的。 大家在中学都学过对数函数,很多伟大的科学家,象玻尔兹曼,爱因斯坦,申农,用这个简单的函数做出了重大的科学突破。在这里,我们用对数函数定义物品的价值。物品的价值定义为 -logbP 其中 P 为物品的稀缺程度,范围从 0 到 1, 0 为极度稀缺, 1 为无限丰富,b 为这个物品的生产厂家数目。我们来看一下这个函数的性质。 首先,一种物品的价值是稀缺程度的递增函数,物品越丰富,其价值越低,如果这种物品无限丰富,也就是P = 1,其价值为零。比如说,空气对我们非常重要,几分钟不呼吸,我们就活不下去。但由于空气无处不在,其经济价值为零。下图是价值与稀缺程度之间的关系。 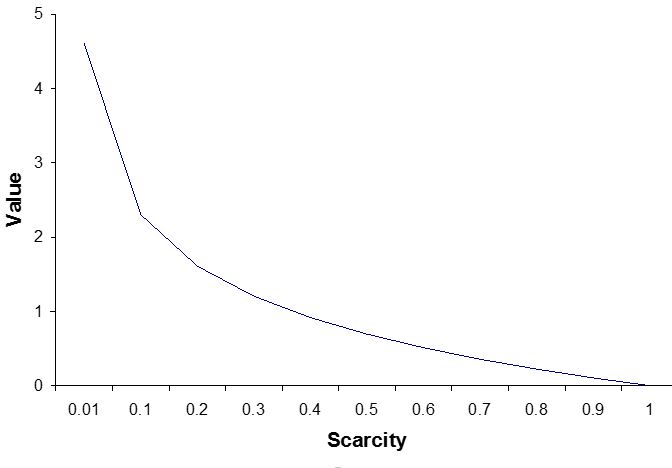
很多人把经济价值等同于对社会的贡献。当今粮价很低,很多人认为农民对社会的贡献低。但如果粮食太贵,有人买不起,很快引发社会动乱。所以很多国家的政府采取各种政策,以保证粮食的充足,同时也造成粮价低廉。很多政府为了保护农民利益,大量补贴农民。从这个价值理论,我们可以清楚看到,经济价值不等同于对社会的贡献。 我们再来分析生产厂家的个数对价值的影响。b 越小,物品的价值越高,下图是物品的价值与生产厂家数目的关系。一样物品,生产的厂家越少,价值越高,大家都知道垄断和寡头经营的行业,利润很高。这个分析不仅可以应用到产品上,也可以应用到任何社会系统,世界上影响力大的宗教,象犹太教,基督教,伊斯兰教,大多是一神教,而佛教和大多数早期的宗教,是多神教,一神教对教徒的控制能力比多神教强很多,当一神教碰到多神教的社会,往往会击败对方。很多职业收入高,往往是由于这些职业由唯一的组织代表。比如说,加拿大所有的医生,都属于同一个医学学会,没有任何竞争;加拿大医生的收费,是统一的,也没有任何竞争;病人看病,必须通过唯一的家庭医生,彼此之间没有竞争。这就是为什么加拿大医生的地位,比中国高很多。我们经常说西方经济是自由竞争的市场经济,但其中最重要的部门,象医疗,教育,军工,以及庞大的政府本身,都由工会和垄断机构控制,很少自由竞争。 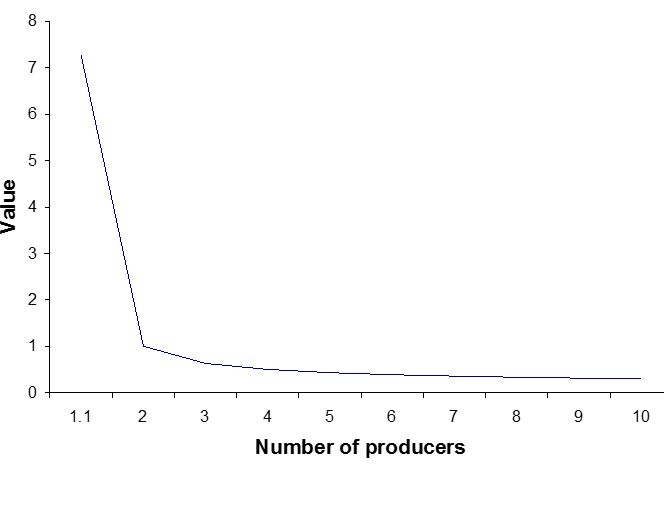 减少选择,对增加价值有决定性的影响。所以几乎所有经济,政治活动,都以减少竞争,增加垄断权力为目的。我们常说的专利法和知识产权保护就是一个例子,知识产权保护最常用的理论是鼓励创新,但创新最多,给消费者带来最多利益的行业,象信息技术,往往是知识产权最自由的行业,而知识产权保护最严格的行业,象生物医学,往往是纳税人花大钱,消费者受益甚少的行业。最近, 很多人讨论无效疫苗和有毒疫苗的问题。疫苗的采用是由政府决定的,由于政府是最强势的垄断机构,这类事情的产生是必然的。 从上面的讨论,我们看到,一个简简单单的对数公式,可以帮助我们深刻了解这个社会中形形色色的活动。很多原本不喜欢数学的学生,也很开心学到对数函数的各种性质。关于这个公式更多的应用,可参看我的文章:价值的熵理论。
An Entropy Theory of Value: Forthcoming in Structural Change and Economic Dynamics
https://www.researchgate.net/publication/228398386_An_Entropy_Theory_of_Value |
