当你站在小溪边看着水流在桥桩下,卵石边的漩涡时,有没有觉得那是一个很特别的东西? 在今天的科学技术水平下,我们对溪中的水流可以说是了解得很透彻了。水流可以看成是无数微小的水“质粒”在经典力学下相互作用,并受着河床和引力的影响而运动。如果我们愿意,我们可以用计算机模拟来重现任何水流的状况,包括漩涡。 但问题是:这样就算了解了漩涡了吗?从微观上来看,水流的速度分布,质量分布在不同小溪中可以说是全然不同,在同一个地方也一直在变化中。但是漩涡就是漩涡,我们不会把它认作别的东西。而且即使你在水里扔块大石头,水流分布肯定是有了很大变化,但那个漩涡仍然存在。是什么原因使得“漩涡”这种东西如此普遍和稳定呢? 如果我们标出漩涡附近各点的水流速度,我们会得到类似于下图的结果。我们一眼就能看出,这个图里有两个漩涡,左面的是逆时针方向,右面的是顺时针。想象一下我们把这张图印在一块橡胶膜上。不管你怎么拉扯让膜变形,我们还是能认出这两个漩涡。那么你怎样让计算机来认出它们呢? 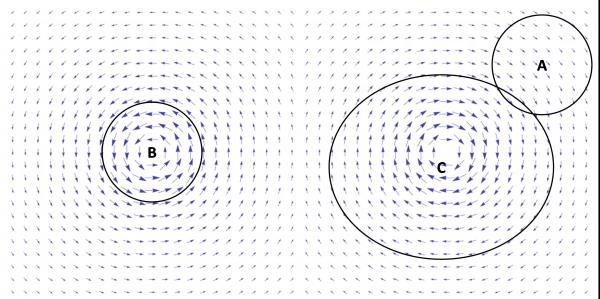
图一:漩涡附近的速度场(部分复制自https://en.wikipedia.org/wiki/Vector_field) 一个办法是考察沿着一个封闭路径的速度方向变化。在图中找一个没有漩涡的地方(如路径A),当我们回到起点时,速度方向的变化是零。在漩涡的周围(如路径B),回到起点时速度方向变化是360度(逆时针绕行时)。而路径C,虽然包围了一个旋转角度相反的漩涡,但速度方向的变化和路径B是一样的。当然我们还可以做进一步的数学分析,但到此为止的观察已经表明了漩涡的三个重要性质。首先,是否有漩涡可以通过一个封闭路径上的速度方向变化来判断。第二,这个判断的结论与路径的选择细节没有关系,而且速度的微小变化也不会影响结果。第三,封闭路径上速度方向的变化一定是360度的整数倍。所以有漩涡和没有漩涡这两种状态不可能通过速度的连续变化来得到,而必须是一个跳跃。也就是说,在外力影响较小的情况下,漩涡不容易产生,但一旦产生了也不容易消失。 从上面的分析我们还看到,漩涡这种现象不是取决于某一点的运动状况,而是一个整体的性质。它对于局部的运动状况并不敏感,而有它自己的“生命”。而且,在水这种连续的介质里,每一个质点的速度和位置都是可以连续变化的。但漩涡却不是连续的:或者是没有,或者是有整数个。对于这种基于整体分布的形状而对局部性质不敏感的东西,有个专门的数学工具来描述和研究它:拓扑学。所以漩涡这种现象也可称作为水流的拓扑现象。 值得一提的是:漩涡这种现象不光是水里有。台风就是大气中的漩涡现象。它一旦形成,就可以稳定地存在几星期,移动上千公里。更推而广之,漩涡这种拓扑现象并不一定要在流体中产生。任何物理量(如磁矩)如果具有角度这样的性质,即增加360后能回到原位,都有可能产生漩涡这样的现象。 2016年物理诺贝尔奖的获奖工作,是研究电子运动中的拓扑现象。因为电子遵循量子力学而且通过电磁力相互作用,它的“漩涡”和水流有很大不同,也更加多姿多彩。而漩涡也只是多种拓扑现象中的一个。 2016年物理诺贝尔奖共发给了三名美国科学家:索列斯(David J. Thouless)得一半,哈尔丹(F. Duncan M. Haldane)和克斯特列兹(J. Michael Kosterlitz)平分另一半。这个奖是表彰他们在材料的拓扑相和拓扑相变方面的理论发现。下面就简单介绍一下他们的三个有关工作。 1970年代初期,索列斯和博士后克斯特列兹提出一种二维体系中新型的相变,后来被称为KT相变。这就涉及到上面说到的漩涡了。当然他们研究的不是水流,而是磁矩,它和水流速度方向一样也是一种角度,所以也能形成漩涡。如上所说,形成一个漩涡是不容易的。但在他们的模型中,形成一对相反方向的漩涡却容易得多,因为他们对于远处的影响抵消了。所以在低温的时候,磁矩漩涡都是成对的。但当温度升高后,这些漩涡对就会“分家”变成单个的漩涡,从而产生相变。虽然这种漩涡本身不能被观测到,但KT相变的理论很好地预言了液氦薄层的超流相变性质,而且后来在其它一些系统中也被观察所证实。 KT相变理论是一个开创性的工作。在此之前,人们都认为二维体系在有限温度下不可能有相变,因为任何有序的结构都不能经受热涨落的颠覆。而KT相变理论的低温相不是通常的“有序”态,而是正负漩涡的“紧耦合”态。而且这种相变只涉及空间相关性的变化而没有对称性的变化,这也与普通的相变不同。所以,可以说KT相变理论给“相变”本身带来了新的研究空间。在这个基础上,人们发展了一套相变理论称为拓扑相变。还有人进一步引入电子态的拓扑性质作为“拓扑序”来定义物质的相。不过关于拓扑序是否属于可观察的物理量,现在还不清楚。 KT相变虽然涉及量子的超流现象,但还是可以借助经典理论来了解。索列斯和克斯特列兹发现漩涡之间的相互作用和正负粒子类似,所以可以借用现成的电磁理论来搞定这个体系。而下一个要介绍的工作,就更加涉及到量子力学了。 霍尔效应在中学物理中都教过。如果把通着电流的导体放在磁场中,它会在垂直于电流和磁场的方向形成一个电压。这是因为运动的电子受到洛仑兹力的影响。原先的电流与这个垂直电压的比就是霍尔电导率。它与磁场强度和导电电子密度有关。这是经典电磁理论就能解释的现象。 但是1980年实验发现,在某些二维电子体系(也就是自由电子被约束在材料表面或界面的体系)中,在变动磁场强度和载流子密度时,霍尔电导率不是连续变化而是阶梯式变化的。也就是说霍尔电导率只能是某些特定的值,而那些值只与某些基本物理常数有关,却与材料的具体性质和实验的条件无关。这被称为“量子霍尔效应”。(量子霍尔效应还有整数分数之分,这里就不详细说了。)霍尔效应的“量子化”本来就够奇怪了,更奇怪的是这种现象是如此普遍(在很多材料中都能观察到)和稳定(即使材料有缺陷和杂质也没关系)。由于量子霍尔效应的发现,有四名物理学家分两次得了诺贝尔奖,其中包括华裔物理学家崔琦(Daniel C. Tsui)。 在量子霍尔效应被发现后两年(1982年),索列斯和同事们就发表了一个理论解释。他们通过基本的量子力学计算,把霍尔电导率表达为一个波函数的积分。然后他们引入一个人造的周期势,以便具体算出波函数和霍尔电导率。最后他们证明了霍尔电导率的量子化,即使在那个周期势趋于零的时候也是如此。后来人们指出,他们提出的那个积分其实就是拓扑学上的“陈数”,所以积分的值总是整数。1985年,索列斯等又发表一篇论文,不再依赖于周期势而是通过边界条件得出了同样的量子化结果。这就表明了量子霍尔效应与波函数的细节无关,而只取决于整个系统的能带结构的拓扑性质和基态的简并度。所以它是相当普适和稳定的。 受到这个见解的启发,另一名得奖者哈尔丹进一步提出了一个及其简约的模型来重现类似现象。顺此思路,人们发现没有外加磁场的情况下也可能存在量子霍尔效应。由于量子霍尔效应伴随着具有超导性质的表面态,这些发现开创了一个新领域:拓扑绝缘体。目前实验上已经证实了了拓扑绝缘体的存在,以及不需外加磁场的“反常量子霍尔效应”。人们希望通过这些奇妙的现象找到性能超群的新型电子材料。值得一提的是,这次诺贝尔奖的官方介绍中对拓扑绝缘体一笔带过,也许别有深意吧。 第三个工作是哈尔丹开创的一维磁性链(例如带磁矩的原子组成的一维链)的研究。哈尔丹指出,一维磁性链中,自旋为半整数和整数的情况有本质的区别。其实加上时间的维度的话,一维磁性链就成为一个二维系统,而哈尔丹的结论和上面第一个工作的KT相变有关。这个结果的一个推论就是:虽然磁性链中间看起来平平无奇(磁矩都抵消了),但相距很远的两头却不能随便乱动(否则就打破了中间的和谐)。所以这两头的磁矩之间就有了量子纠缠。这种纠缠是拓扑性质决定的所以比较稳定。自然而然地,这就给量子计算机带来了新的思路。 凝聚态物理的拓扑理论发展过程中,华裔和中国科学家做出了不少重要贡献。上面说到的索列斯1985年关于量子霍尔效应的文章,两个合作者都是华人:当时索列斯的的学生牛谦和做高能物理的吴咏时(牛还是该论文的第一作者)。在诺贝尔委员会提供的得奖工作官方介绍中还提到了好几个华人科学家的工作:美国华人物理学家文小刚关于拓扑序基础理论的工作,中科院物理所和清华大学物理系团队实验观测到量子反常霍尔效应的工作,以及最近包括北大和中科院的几个中外研究单位合作的发现固体中威尔费米子(Weyl Fermion)的工作(作为得奖工作的一个推论)。而量子霍尔效应理论中涉及的“陈数”(Chern number), 就是归功于华人数学家陈省身了。另外值得一提的是,拓扑材料的研究最近在中国很受青睐。薛其坤教授因为其实验证实量子反常霍尔效应等工作在2016年(诺贝尔奖宣布之前)获得中国的“未来科学大奖物质科学奖”。所以,继2015年中国科学家屠呦呦获得诺贝尔生理学或医学奖之后,2016年又是诺贝尔奖史上中国科学界值得骄傲的一年。 这三个得奖工作都是在上世纪七,八十年代完成的。当时凝聚态物理可说是在一个转折点。在那以前,凝聚态物理基本是基于自由电子在晶格形成的外场中的运动。其它的相互作用(电子之间的耦合,电子自旋和轨道的耦合,电子运动与晶体震荡的耦合等)都是作为微扰来处理。到了七,八十年代,这种方法遇到了很多困难。一些重要的物理现象(包括高温超导)看来不能用微扰来解释,而需要更加注重整体,而不是单点子状态的新的数学工具。当时在凝聚态物理中引入新数学有很多尝试,如超过三维的空间解决准晶体问题(quasicrystal),渗流(perculation),分形(fractal),混沌(chaos),阻挫(frustration) 等。当然其中有些工具并非针对整体现象。其中大多数努力得到的结果都是很有限的,但这又显然是凝聚态物理的出路,所以这个方向的探索一直在进行。现代的凝聚态物理的活跃领域如强耦合(strong coupling),演生现象(emergent phenomena)等都是如此。从这方面来说,2016年诺贝尔奖表彰的拓扑态工作应该算是引进新数学比较成功的一个例子。但也需要指出,即使这几个工作,虽然涉及的是体系的拓扑性质,但借助拓扑学数学结果的地方并不多。其中和拓扑学数学联系最紧密的是量子霍尔效应的工作(量子霍尔系数与某个纤维丛的陈数有关)。但这个联系也是在索列斯的工作发表后其他人领悟到的。而且拓扑材料的研究虽然最近很热而且有不少很有趣的结果,但它的应用范围只是凝聚态物理中的一小部分而并非整个凝聚态物理的框架。所以,对凝聚态物理,乃至整个现代物理来说,寻找合适的数学工具仍然是一条漫漫长路,还有很多发现和创新的机会等待着热爱数学的物理学家们。 本文得到多位有关方面专家审阅指正,作者深表感谢。文责由作者本人承担。 有关博文: 神秘的中微子—2015年物理诺贝尔奖介绍 http://blog.creaders.net/u/1030/201602/248750.html http://blog.sciencenet.cn/blog-309766-956906.html 换灯泡,得诺奖:2014年诺贝尔物理学奖介绍 http://blog.creaders.net/fouyang/user_blog_diary.php?did=213800 http://blog.sciencenet.cn/blog-309766-878651.html 半个世纪后的大奖:2013年诺贝尔物理奖介绍 http://blog.creaders.net/fouyang/user_blog_diary.php?did=204606 http://blog.sciencenet.cn/blog-309766-861376.html 衔接量子与经典物理:2012年物理诺贝尔奖介绍 http://blog.creaders.net/fouyang/user_blog_diary.php?did=146660
谈谈2011年物理诺贝尔奖:成功的道路很多条 http://blog.creaders.net/fouyang/user_blog_diary.php?did=104374
石墨烯的传奇:2010年诺贝尔物理奖介绍 http://blog.creaders.net/fouyang/user_blog_diary.php?did=81822
诺贝尔物理奖介绍2009: 闲谈CCD http://blog.creaders.net/fouyang/user_blog_diary.php?did=55767
诺贝尔物理奖介绍2009: 闲谈光纤 http://blog.creaders.net/fouyang/user_blog_diary.php?did=54652
对称破缺之美:2008年物理诺贝尔奖工作介绍 http://blog.creaders.net/fouyang/user_blog_diary.php?did=93171 诺贝尔物理奖介绍2007:巨磁阻和自旋电子学 http://blog.creaders.net/fouyang/user_blog_diary.php?did=74278
|
