在一个普普通通的定义上较劲，却又不肖理会一下整个数学界的基本共识。这就是中国人的任性之处。事实上，在所有的真命题当中，能够满足其逆命题也为真的比率应当等于零（溪大炮知道为什么吗？）。这样的东西很少，毕德格拉斯定理（勾股定理）恰好是这样的一个定理，即其逆定理也成立。因此，溪大炮的说法纯属瞎掰。不过，俺挺喜欢溪大炮的，就像革命党人喜欢孙大炮的道理差不多。
以下是网上（http://mathworld.wolfram.com/Theorem.html）关于定理（theorem）的定义，并没有要求其逆定理也必须成立，才配称为定理一说。 A theorem is a statement that can be demonstrated to be true by accepted mathematical operations and arguments. In general, a theorem is an embodiment of some general principle that makes it part of a larger theory. The process of showing a theorem to be correct is called a proof. Although not absolutely standard, the Greeks distinguished between "problems" (roughly, the construction of various figures) and "theorems" (establishing the properties of said figures; Heath 1956, pp. 252, 262, and 264)。 According to the Nobel Prize-winning physicist Richard Feynman (1985), any theorem, no matter how difficult to prove in the first place, is viewed as "trivial" by mathematicians once it has been proven. Therefore, there are exactly two types of mathematical objects: trivial ones, and those which have not yet been proven. The late mathematician P. Erdős has often been associated with the observation that "a mathematician is a machine for converting coffee into theorems" (e.g., Hoffman 1998, p. 7). However, this characterization appears to be due to his friend, Alfred Rényi (MacTutor, Malkevitch). This thought was developed further by Erdős' friend and Hungarian mathematician Paul Turán, who suggested that weak coffee was suitable "only for lemmas" (MacTutor, Malkevitch). R. Graham has estimated that upwards of 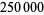 mathematical theorems are published each year (Hoffman 1998, p. 204). |
