天道运数：活命之数（二）

雨斤

上篇侃了个生命之数：欧拉常数e. 今天再来侃侃一个活命之数：圆周率π.

为什么称它为活命之数呢？

因为，你要想活命，就得磨去棱角，变得圆滑些。这既是宇宙天体的通行法则，也是人类社会的处世之道。

根据宇宙大爆炸理论，不管一个天体最初的形状为何，也不论个头大小，经过亿万年漫长的演化旋转，最后一个个都变成了圆球体。

人也一样。年轻时，愣头青小伙子一个。口无遮拦，率真爽快，棱角分明。但随着年岁的增长，经验的积累，你终于也变得谨言慎行。话未出口，三思而行。遇着看不惯的人和事，也得过且过，多一事不如少一事。明哲保身，处世圆滑了！

所以，不管是天体星球，还是人类动物，一旦和“圆”沾上边，你就和π沾上边了。这不是活命之数，是什么？

事实上，圆形是自然界最普遍的物体形状。你仰观日月，俯看树木断面，圆形无处不在。人类最早的发明，就是利用圆形的滚动原理而制成的车轱辘了！英语谚语：You don't need to reinvent the wheel. 就是这个意思，那个发明早有了！

世界各地的原始先民们，早就注意到了圆形物体的周长和直径之比，大约是三比一。“周三径一”这句话，在中国商朝时已经广为人知，殷墟甲骨文里就有卜辞提到。古巴比伦人也早就知道此事。公元前1900年的一件木板上，巴比伦人就记载有3.125.公元前1650年的兰德草纸上，古埃及人也记载有3.1605.在中国的秦汉之交时期，希腊的阿基米德 (287-212 B.C.)把π的数值精确计算到了3 1/7 和3 10/71之间.

然而，提起圆周率，你就不能不提祖冲之。

祖冲之（429-500）是中国南北朝时期的数学家。他在刘徽的基础上，发明了“割圆术”，首次将“圆周率”精算到小数点后第七位，即在3.1415926和3.1415927之间。世人称之为“祖率”。祖率在其后的一千二百年间，一直是世界上最精确的圆周率。直到16世纪，阿拉伯数学家阿尔·卡西才打破了祖冲之创造的小数点后第七位这一纪录。

在美国，为了强调π的重要性，麻省技校每年在3月14日下午15时9分零2秒放榜，用电邮通知录取的新生名单。想爬藤的孩子，对这个时刻可是刻骨铭心的！

那么，活命之数与上回的那个生命之数之间有什么关联没有呢？

有！这就是著名的欧拉等式。有人甚至认为，这个公式是数学里最具美学价值的等式。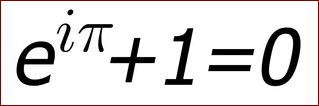

注意，这个等式把数学里最著名的三个数字联系起来了：e,π,i.

还有的洋人发明了一种巧记π的方法：口里念念有词的说："May I have a large container of butter today"。然后，数一数这句话里每个单词里的字母个数，就得到：3 1 4 1 5 9 2 6 5。哈哈哈，妙吧？

精确计算π的方法，可用泰勒级数把反正切函数tan^-1(x)在x=1处展开，就得到：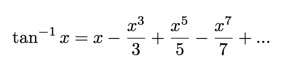

π／４　＝　１－１／３　＋１／５－　１／７　＋　１／９　－　１／１１　＋　... ...

两边同乘以4, 即为：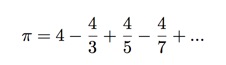

1882年，德国人佛迪南·林德曼证明圆周率π，是个超越数。当然，π也就更是个无理数了。

黑人兄弟虽然不懂这些猫腻，但也同意π是他们的活命之数：吃匹萨能活命，而匹萨是圆的。

哈哈哈，周末了，开个玩笑嘛。下篇再侃另一个天道运数（三）。