天道运数：美命之数（三）

雨斤

前文侃完“生命之数”与“活命之数”，今天再接着侃一个“美命之数”。

何谓美命之数？顾名思义，就是最符合美学原理的数字。比方说，你要在讲台桌子上摆放一盆花。摆在桌子的什么位置，最好看呢？

有人可能说了，放在桌子中心位置不就得了。

非也。花摆在桌子的中心位置，那让讲话的人站在何处？事实上，花摆在桌子的中心位置，一点也不好看，显得呆板，也有些喧宾夺主。

正确的答案是：摆在桌面前后的61.8%和左右的61.8%交汇处，最好看。

眼尖的人可能已经认出来了：这不就是黄金分割点么？

对头。这在数学上是有推导证明的。如图：一个矩形的边长为 a 和 a + b ,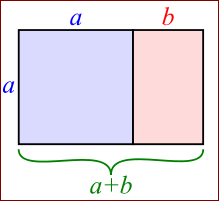

假设 a > b.我们要求长边与短边之比，等于长加短之和与长边之比，就得到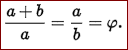

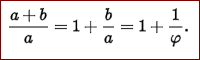
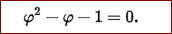
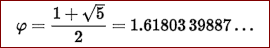
文革期间，华罗庚当年为了响应伟大领袖的五七指示，带领数学所的人员下乡，大力推广的优选法，搞的就是这个玩意儿。只不过，他把1.618减去一，变成了0.618.

事实上，华老用的是黄金比率的反比，因为 1/1.618 = 0.618。也就是通常所说的短边与长边之比 b/a：　a/b - 1 = b/a。

需要指出，这个黄金比率1.618...显然不是个超越数，而是个代数数。当然，它也不是个有理数，是个无理数。

那么，这个数字是不是“人为”的呢？(此乃克朗涅克尔之问也！)

不是的。这个数字大量存在于自然界。因此，我才在这里称它是个“天道运数”。

人们早已发现，植物叶子的形状，雪花的几何图形，人脸形状，瓜子脸，都符合这个黄金比率。据此，工程师们和艺术家们在设计中，也大量运用了这个比率：手机屏幕，电脑屏幕，电视机屏幕，电影银幕，杂志封面，连打印机的A4纸张，等等。

华老当年的一大发明，就是把黄金比率运用于随机抽样中。理论和实践都证明，运用黄金比率进行的随机抽样，从概率上讲，最有可能在最短时间内，最少的抽样次数下，取得最优的结果。因此，现在海关人员抽查入关的旅客行李，也是运用黄金比率来随机抽样，打开箱子。

近年来，医学界也运用大数据发现，血压符合黄金比率的人最健康：也就是你的高压（收缩压）和低压（舒张压）之比最好是1.618.

营养学家也认为，最健康的膳食比例，就是符合黄金比率的碳水化合物比上蛋白质／脂肪：52% 碳水化合物，20% 蛋白质，28% 脂肪。

黄金比率在音乐里也有应用。印象派大师德彪西的名曲《水中倒影》（Reflections in Water），就是用黄金比率写成的。

最后，再来解释一个黄金比率与生命现象的关系。

众所周知，斐波那契数列最初是用来描述兔子的繁殖的：

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... ...

令人惊奇的是，斐波那契数列的后一项与前一项之比: F_{n}/F_{n-1}，当n趋于无穷大时，的极限正是黄金比率1.618...。这个是有严格的数学证明的。

至于证明，在此就免了吧。