數學翻譯的信達雅（二）

雨斤

前文（·李善蘭的信達雅）說了“微分”、“積分”譯文的信達雅。

1854年，28歲的黎曼在德國哥廷根大學發表就職演講。他在演講里，給一種能多度延展的幾何對象起了一個新名稱，德文寫作 mannigfaltigkeit, 英文翻譯為 manifold。英文字面意思可以理解為 “多層”、“多重”、或“各式各樣的形狀”，等等。

整整一百年後的1954年，中國第一個拓撲學家江澤涵先生，把這個詞翻譯為 “流形”。

江先生博古通今，學貫中西。他雖然只是一個數學家，但他的古文功底也是十分的了得！尤其是，他把南宋民族英雄文天祥的正氣歌爛熟於心。這裡把Manifold的中文，翻譯成“流形”，就取自文天祥的《正氣歌》：“天地有正氣，雜然賦流形”。

正氣歌（節選）

南宋  文天祥

天地有正氣，雜然賦流形。

下則為河嶽，上則為日星。

於人曰浩然，沛乎塞蒼冥。

皇路當清夷，含和吐明庭。

時窮節乃見，一一垂丹青。

在齊太史簡，在晉董狐筆。

在秦張良椎，在漢蘇武節。

為嚴將軍頭，為嵇侍中血。

事實上，文天祥的這個“流形”的用法，其原始出處為《易經》：“大哉乾元，萬物資始，乃統天。雲行雨施，品物流形。”

洒家以為， 江澤涵的這個翻譯比英文原文更加符合黎曼的原意，即：多樣化的形體。另外，流形的“流”字，還暗含有“光滑”之義，而這正是黎曼的manifold所具有的性質。江先生的翻譯，完美的體現了嚴復所說的“信、達、雅”，實在是高明之至。

為什麼這麼說呢？

因為黎曼定義的“n維流形”大概是這個樣子的：以其中一個點為基準，則周圍每個點的位置都可以用 n 個實數來確定。後人將這種性質總結為：流形的局部與 n 維歐氏空間的局部具有相同的拓撲性質。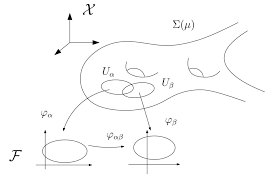

如果進一步要求在流形的不同局部做微積分的結果可以互相聯繫起來，成為“整體微積分”，則稱此流形為“微分流形”。

一個簡單的例子就是二維球面。我們都知道，二維球面上沒有整體適用的坐標。經度和緯度是一組很好的坐標，但是在南北兩極，經度和緯度則無從定義。儘管如此，球面的每個局部都可以畫在平面上，這就是地圖。把各個區域的地圖收集在一起，重疊的部分用比例尺協調一下，就得到整個球面。這樣，坐標（或地圖）只存在於每個局部，而整個球面其實是地圖之間的重疊關係。球面是二維流形，因為球面的局部同平面（二維歐氏空間）的局部具有相同的延展性質。球面的整體結構顯然跟平面不同。沿着球面的某個方嚮往前走，比如，從赤道某點出發往東走，最終會回到出發點。而如果在平面上沿某個方嚮往前走則永遠也不會回到出發點。研究流形的整體結構，以及整體結構與局部結構之間的關係，就是 “微分拓撲學” 的核心課題。

獨家原創，版權所有。未經作者同意，請勿轉載。